Find a tangent point on circle?

Question

Given a line with first end point P(x1,y1) another end point is unknown, intersect with a circle that located at origin with radius R at only one point(tangent) T(x2,y2). Anyone know how to get the point T? Thanks in advance!

Involved

how is it a line if you have only one end point given? – Cirrose

he does have two different endpoints because he knows the line is tangent. – Selfsustaining

dmindreader you really get my point. Thanks. – Involved

this is math-, not programming-related – Cute

Answer 1

Given a line with first end point P(x1,y1) another end point is unknown, intersect with a circle that located at origin with radius R at only one point(tangent) T(x2,y2). Anyone know how to get the point T?

Some of the other solutions seem a little like overkill. I think the simplest way is just to notice that this is a right triangle, with vertices P, T, and O (the origin). The angle PTO is the right angle, because a tangent line is always at a right angle to a radius.

You know the length of TO because it's of length r and has a vertex at the origin; you know OP because you know where O and P is. Given two sides of a right triangle, it's easy to find the length and direction of the third side. This is homework, so I'll leave the rest as an exercise to the reader.

                    __...------__    T(x2, y2)                      
               _.-''             -(+)
            ,-'                   |----             
          ,'                     |     ----
        ,'                      |       '  ----
       /                       |         `     ----       
      /                       |           `.       ----   
     /                       |             \           ----
    |                       |               |              ----
    |                      |                 |                  ----
    |                     |                  |                      ----
    |                   (+)---------------------------------------------(+) P (x1,y1)
    |                                        .'        
    |                    O                   |         
     |                                      .'         
      \                                     /          
       \                                  ,'           
        `                                /             
         '.                            ,'              
           '-.                      _,'             
              '-._              _,(+)  T'(x3, y3)                   
                  '`--......---'                       

There are two possible directions for TO, since the point T' is also a valid tangent point, so you will have two congruent triangles.

Enchantment

This is known as the Thales' theorem. – Litharge

@JCM I fail to see how this is Thale's theorem. Thale would only state that OP is the diameter of the circumcircle for OPT. – Gorham

This does not look like a right triangle. In fact, the points T and T' will be different depending on how close to the circle point P is, and hence angles will be different too. I fail to see what for this answer got so many upvotes. – Eley

That's correct, because that's how tangent lines work. A tangent line (PT) is always perpendicular to the radius of the circle that connects to the tangent point (T). It is therefore guaranteed to be a right triangle. The angles TOP and OPT will be different, but PTO will remain a right angle. Try it and see yourself! – Enchantment

Note for readers: don't forget that ∠OTP is 90 degrees so you can find the T using Pythagorean [just in case anyone forgot about this for a moment] – Delorisdelorme

Answer 2

All you need is in dmckee's answer, but if you care for some code check this implementation using Javascript and HTML canvas.

Full example: http://jsfiddle.net/zxqCw/1/

// find tangents
dx = cx - px;
dy = cy - py;
dd = Math.sqrt(dx * dx + dy * dy);
a = Math.asin(radius / dd);
b = Math.atan2(dy, dx);

t = b - a
ta = { x:radius * Math.sin(t), y:radius * -Math.cos(t) };

t = b + a
tb = { x:radius * -Math.sin(t), y:radius * Math.cos(t) };

Uninhibited

What does x:radius represent? – Saffier

radius = radius of the circle. ta = an object with properties x and y (basically a point). To answer your question, x:radius doesn't represent much on its own. The code is defining the value of ta.x where x = radius * Math.sin(t). Please make sure you refer to the jsfiddle to see a working example. – Uninhibited

I am trying to convert this to C# code.... and I couldn't figure out what x:radius is... But I read the code wrong.... I misunderstood it for being an object x with value radius ... where it was simply the value x of ta. THanks ;) – Saffier

The call to atan2 call is not needed as b is just pi/2 - a. – Ample

@Ample uhh proof? not one single person is doing that, so I'd like to see evidence that this is the case. – Kerbstone

@Ample actually you may be right, at least in the case you only need the length of the tangent, it doesn't matter the origin of your point, you can set it manually, the only thing that matters is distance, if you choose x = 0.0, and y = distance from circle for your point P, then atan2(y, x) = pi/2 as atan2(inf) = pi/2, since 1/0 = infinity. – Kerbstone

This works if cx and and cy are both 0. However, if the circle is not centered at the origin, this needs to be accounted for by adding the center coordinate to the tangent points: ta = { x:radius * Math.sin(t) + cx, y:radius * -Math.cos(t) + cy}; t = b + a tb = { x:radius * -Math.sin(t) + cx, y:radius * Math.cos(t) + cy}; – Stockstill

Answer 3

Take R as the radius of the circle and D the distance from the external point to the center of the circle such that D > R.

The tanget line makes and angle of \alpha with the line connecting the external point and the center, where

\alpha = arcsin(R/D)

The line connecting the external point (P) and the center (C) makes an angle with the horizontal of

\beta = arctan((C_y - P_y)/(C_x - P_x))

That gives you the angle of the tangent line with the horizontal as

\theta = \beta +/- \alpha

Note the ambiguity.

The length of the tangent segment is

L = sqrt(D^2 - R^2)

which is all you need.

Graphology

@HanWu: On drawing a picture and checking myself, I still get arcsin. You would use arccos for the angle between the connecting line (CP) and the radius (CT). – Graphology

arcsin is correct: sine (alpha) = opposite (R) / hypotenuse (D) – Cute

\alpha = arcsin(R/D) should be \alpha = arccos(R/D) – Involved

I was thinking about it, and it seems to be incorrect. Specifically, there is no configuration in which some sine would be equal to R/D (nor a cosine). You want D to be a hypotenuse, but hypotenuse is only defined for right triangle, and however right triangle you make with the tangency point and some point on D — the hypotenuse would always be the line from tangency point to the external point as it's always bigger. – Eley

there is soo much suspect with this answer... especially length. – Kerbstone

I may have failed to communicate correctly, but the math is sound. In term of the figure in John's answer, R is the length of the segment OT, D is the length of the segment OP, alpha is the angle OPT, and L is the length of segment TP. It checks. – Graphology

Answer 4

imbrizi's answer assumes that the circle's center is (0,0).

This is the correct answer in Objective C:

- (NSArray *)pointsTangentToCircleWithCenter:(CGPoint)centerPoint
                                      radius:(CGFloat)radius
                                  outerPoint:(CGPoint)outerPoint {

    float dx = centerPoint.x - outerPoint.x;
    float dy = centerPoint.y - outerPoint.y;
    float dd = sqrt(dx*dx + dy*dy);
    float a = asinf(radius / dd);
    float b = atan2f(dy, dx);
    float t1 = b - a;
    CGPoint tangentPoint1 = CGPointMake(centerPoint.x + radius*sinf(t1), 
                                        centerPoint.y + radius*-cosf(t1));

    float t2 = b + a;
    CGPoint tangentPoint2 = CGPointMake(centerPoint.x + radius*-sinf(t2), 
                                        centerPoint.y + radius*cosf(t2));

    NSArray *points = @[
                        [NSValue valueWithCGPoint:tangentPoint1],
                        [NSValue valueWithCGPoint:tangentPoint2]
                        ];
    return points;
}

Tetartohedral

Answer 5

1. You can find direction of vector DX if you rotate vector DO by angle alpha (angle alpha is found as asin(len(OX) / len(DO)), which is simply arcsinus of radius over hypotenuse)

2. You can find the length of vector DX trivially as following: sqrt(len(DO)*len(DO) - len(OX)*len(OX))

3. Given the direction and length of vector DX, you can find the value of point X. One approach would be to normalize DX and multiply it by the length of it.

auto dist = D.Distance(O);
auto side = sqrt(dist*dist - rad*rad)
auto line = Vector2D(D, O);
line.Rotate(asin(rad / dist)); //get the direction
line.Normalize();              //set length to 1
line*=side;                    //we have the direction, now get length
Point2D X = D + line;

P.S. Note that there is also a second tangent, which is found by rotating DO by minus alpha

Alves

Answer 6

It is not obvious to me that this is homework, but I do like the intuition that a right triangle is defined. Even so, there will be some algebra with that solution.

Another approach that seems viable is to simply define the problem as the solution of two equations in two unknowns. That is, the equation of a circle, centered at (0,0), with radius R is

x^2 + y^2 = R^2

The equation of a line that passes through the point (xt,yt), with (unknown) slope S is

(y - yt) = S*(x - xt)

Solve the system of two equations for the intersection point. Depending upon the value of S, there will be zero, one or two solutions to this pair of equations. It will also turn out that there are two values of S such that the solution is unique. Solve for those two values of S that make the solution unique, then recover the intersection point (xt,yt). I won't go through the actual solution in depth in case this is homework, but that part is trivial algebra.

My point is that this algebraic approach is another way to view the solution of the computational geometry problem. It highlights an interesting point in that there are two lines which intersect the circle at a tangent point, and that when a line intersects at a tangent point, there is a single point of intersection.

A flaw of this approach is that is fails due to a singularity for SOME problems. I.e., when the line with slope S is vertical, then S is undefined. Other approaches that rely on simple distances and the Pythagorean theorem are robust to that event.

Cannady

Answer 7

Here is a C# solution (it can be easily adapted to other languages) that doesn't use trigonometric functions, only geometric construction.

You can see a living representation here (P, C and radius can be moved): https://www.desmos.com/calculator/ifzt2nzyl9

public static double[] GetTangentPoints(
    double px,
    double py,
    double cx,
    double cy,
    double radius)
{
    var points = new double[4];

    var dx = cx - px;
    var dy = cy - py;
    if (dx == 0 && dy == 0)
        return null; // no solution

    // PC is distance between P and C, pc2 is PC^2
    var pc2 = dx * dx + dy * dy;
    var pc = Math.Sqrt(pc2);
    if (pc < radius)
        return null; // no solution

    // R is radius of  circle centered in P, r2 is R^2
    var r2 = pc2 - radius * radius;

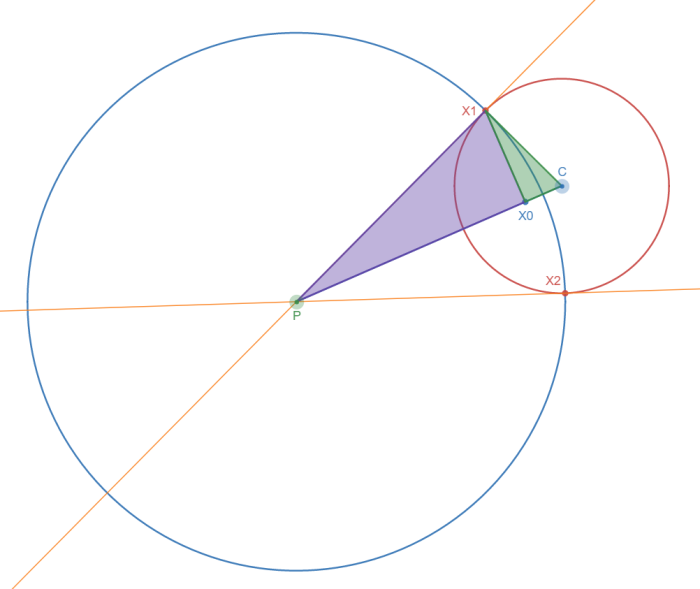
    // d is the P => X0 distance (demonstration is here https://mathworld.wolfram.com/Circle-CircleIntersection.html where PC is named 'd' in there)
    var d = r2 / pc;

    // h is the X0 => X1 (and X0 => X2) distance
    var h = Math.Sqrt(r2 - d * d);

    // first tangent point
    points[0] = px + (dx * d - dy * h) / pc;
    points[1] = py + (dy * d + dx * h) / pc;

    // second tangent point
    points[2] = px + (dx * d + dy * h) / pc;
    points[3] = py + (dy * d - dx * h) / pc;

    return points;
}

Multivalent

Answer 8

Use the x,y coordinates of the intersecting equations (the one of the circle and the one of the line). That's the point.

If you have only one end point from which to draw the line you'll get two different points, as there will be two different tangent lines, one up and one down.

Selfsustaining

Answer 9

I usually use Maple software to solve such problems. It can even generate C code from those equations.

Here's the output:

t1 = v_x * v_x;
t2 = t1 * t1;
t3 = v_y * v_y;
t6 = sqrt(t1 * t3 - t1 + t2);
t7 = v_y + t6;
t9 = 0.1e1 / (t1 + t3);
t13 = 0.1e1 / v_x;
x1 = -(t7 * t9 * v_y - 0.1e1) * t13;
y1 = t7 * t9;
t16 = (-v_y + t6) * t9;
x2 = -(-t16 * v_y - 0.1e1) * t13;
y2 = -t16;

Obviously, you need to add float or double to the variables, also check for negative value before taking the square root.

Blockage

Answer 10

Another solution; less elegant than dmindreader`s, but maybe simpler to understand:

You know that the point T is on the circle and that the line OT is perpendicular to the line PT

that gives you

abs(O - T) = R
dotProduct(O - T, P - T) = 0

Shaddock

Answer 11

Here is my C# answer. Just 7 lines of code. You have to watch "Youtube A Miraculous Proof (Ptolemy's Theorem) - Numberphile" to figure out how it works. The code is tested and produces the correct answers. Sorry about the inserted line feeds. I just copied from Visual Studio to here.

    static void FindTangentPoints(float r, PointF p, out PointF tangent1, out PointF tangent2)
    {
        float incidentLength = MathF.Sqrt(p.X * p.X + p.Y * p.Y); //the distance from the origin to the point outside the circle
        
        float reflectedLength = (r * r) / incidentLength; //see Youtube A Miraculous Proof (Ptolemy's Theorem) - Numberphile           
                                                          //take particular note when Prof Stankova writes OA1 * OA = R*R            
        PointF p2 = new PointF(p.X * reflectedLength / incidentLength, p.Y * reflectedLength / incidentLength);  //the inversion in the plane of pointOutsideTheCircle

        float pRadians = MathF.Atan2(p.Y, p.X); //the same as the angle to point p2 

        float angleP2OT = MathF.Acos(MathF.Sqrt(p2.X * p2.X + p2.Y * p2.Y) / r); //the angle between the tangent point and p

        tangent1 = new PointF(r * MathF.Cos(pRadians + angleP2OT), r * MathF.Sin(pRadians + angleP2OT));
        
        tangent2 = new PointF(r * MathF.Cos(pRadians - angleP2OT), r * MathF.Sin(pRadians - angleP2OT));
    }

Overcasting