Solving large linear systems with block sparse matrices

Question

I want to solve Ax = b where A is a very large square positive definite symmetric block matrix and x and b are vectors. When I say large I mean for a nxn matrix an n as large as 300,000.

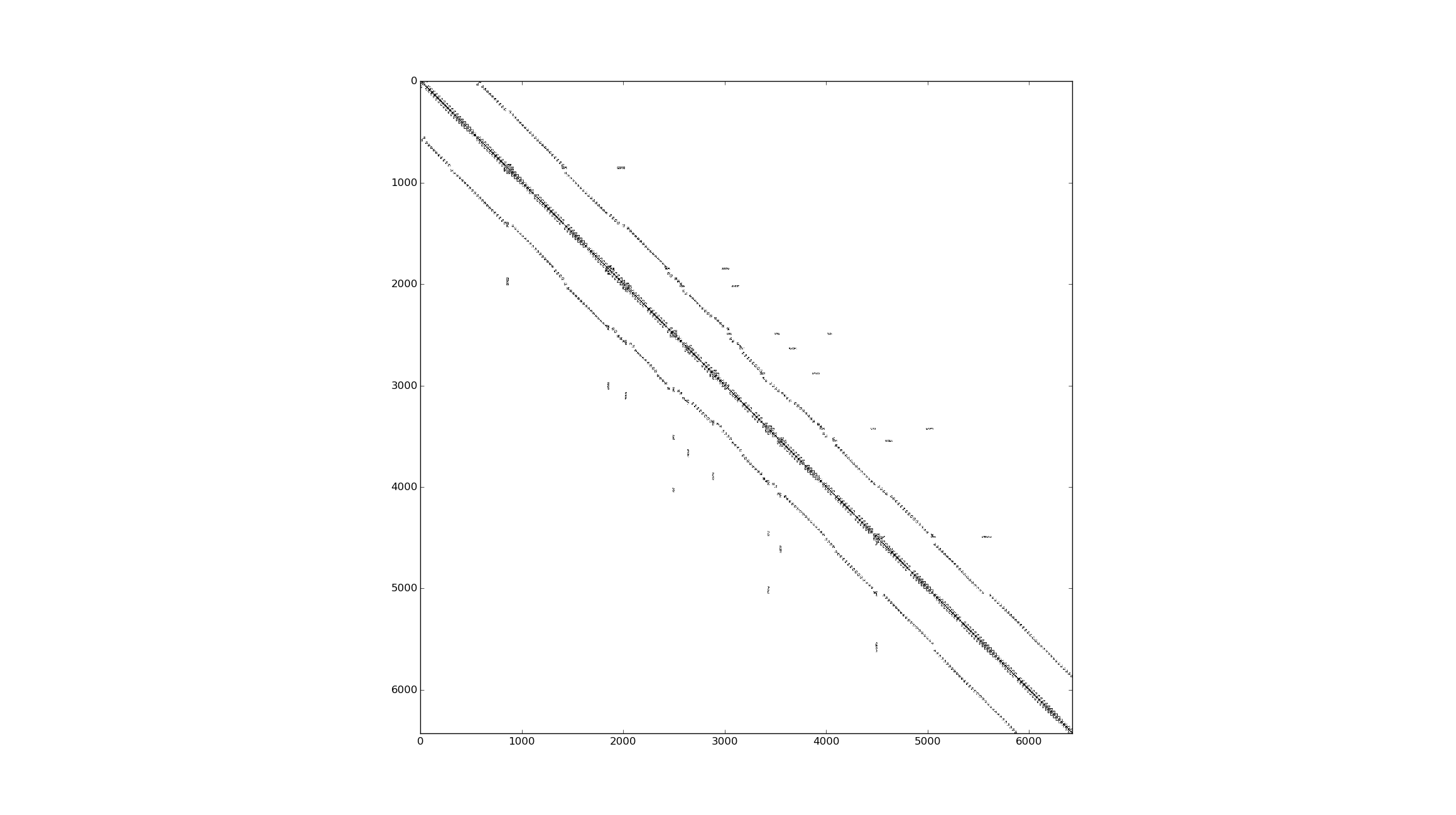
Here is an example of a much smaller but representative matrix I want to solve.

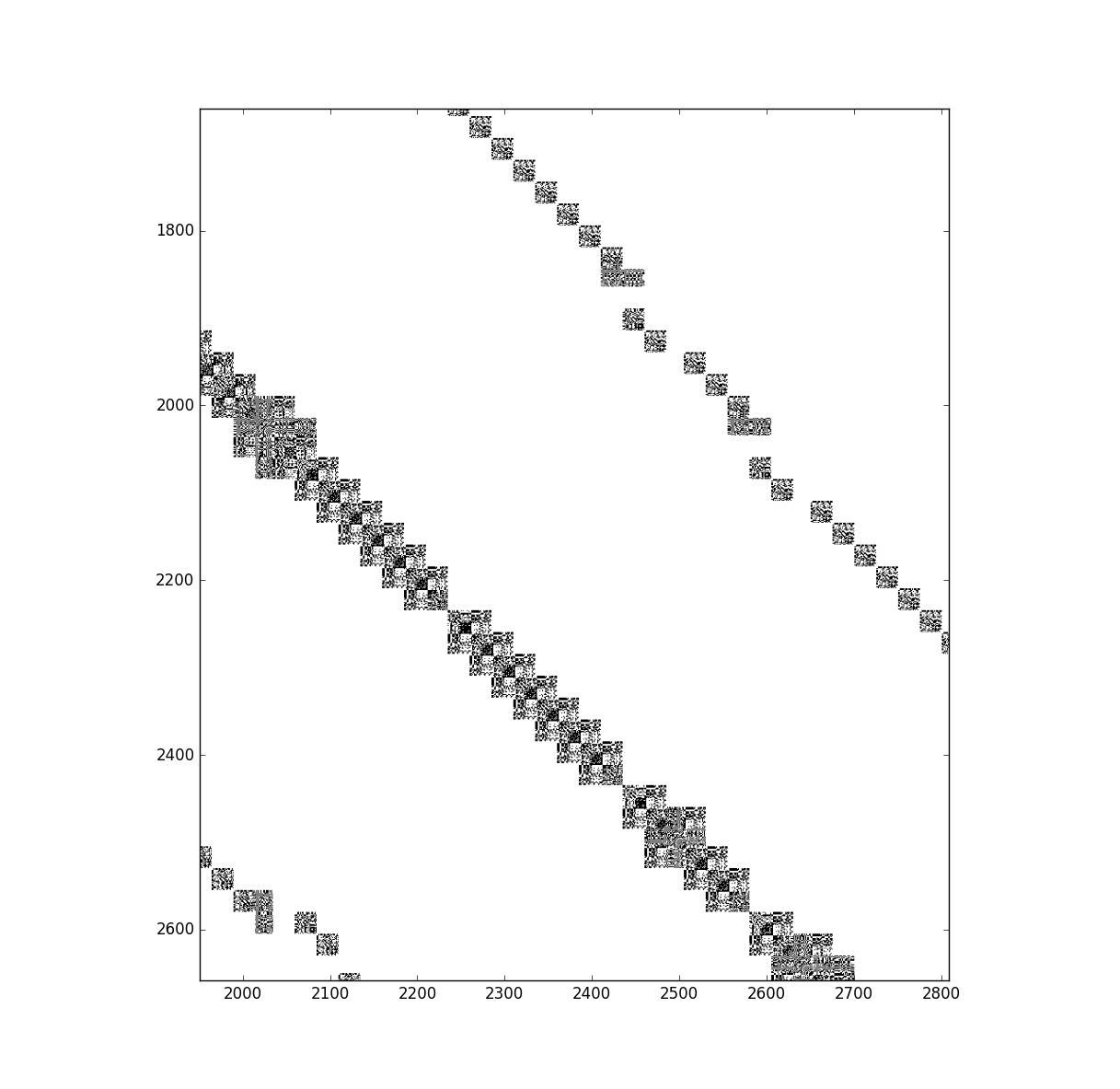
And here is the same matrix zoomed in showing that it is composed of blocks of dense matricies.

I previously (see here, here, and as far back as here) used Eigen's Cholesky solver which worked fine for n<10000 but with with n=300000 the Cholesky solver is too slow. However, I did not take advantage of the fact the I have a block matrix. Apparently, there exists algorithms for solving sparse block matrices (e.g. block cholesky factorization).

I would like to know specifically if Eigen has optimized algorithms, using factorization or iterative methods, for sparse dense block matrices which I can employ?

Also can you suggest other algorithms which might be ideal to solve my matrix? I mean as far as I understand at least for factorization finding a permutation matrix is NP hard so many different heuristic methods exist and as far as I can tell people build up an intuition of different matrix structures (e.g. banded matrix) and what algorithms work best with them. I don't have this intuition yet.

I am currently looking into using a conjugate gradient method. I have implemented this myself in C++ but still not taking advantage of the fact that the matrix is a block matrix.

//solve A*rk = xk
//Eigen::SparseMatrix<double> A;
//Eigen::VectorXd rk(n);
Eigen::VectorXd pk = rk;

double rsold = rk.dot(rk);
int maxiter = rk.size();
for (int k = 0; k < maxiter; k++) {
    Eigen::VectorXd Ap = A*pk;  
    double ak = rsold /pk.dot(Ap);
    xk += ak*pk, rk += -ak*Ap;      
    double rsnew = rk.dot(rk);
    double xlength = sqrt(xk.dot(xk));
    //relaxing tolerance when x is large
    if (sqrt(rsnew) < std::max(std::min(tolerance * 10000, tolerance * 10 * xlength), tolerance)) {
        rsold = rsnew;
        break;
    }
    double bk = rsnew / rsold;
    pk *= bk;
    pk += rk;
    rsold = rsnew;
}

Will

Do you really want to implement this on your own? Maybe you should try some available libraries doing this kind of stuff? E.g. elemental. – Chartulary

@sascha, I am happy to use libraries, I am already doing that with Eigen (except for a custom conjugate gradient method), but I would consider others if Eigen is not sufficient for this case. – Will

Eigen sounds like a basic Linear Algebra to me, without (more complex; structure-using) optimization algorithms per se. But i never used it. While i also have no experience at all with elemental, i do think that the stuff you are doing is somehow possible (and probably highly optimized). Sadly, there are no more hints i could give you. Maybe have a look at this part of the docs. Good luck! – Chartulary

@sascha, the problems with libraries, at least with Eigen, is I have additional information because I know much more about how the matrix is made, and this information can by employed. For example the block structure of the matrix. As far as I know Eigen just sees a sparse matrix not a sparse block matrix. – Will

a) I have heard great things about Intel MKL Pardiso, if you license allows it, you may try that. b) CG depends extremely on its preconditioner, which again depends on the exact system you want to solve. It can make the difference between 1000s and 10s of iterations to convergence and is definitely worth looking into. – Dorey

@BaummitAugen, we may purcahse MKL. But before that I am looking for some general knowledge. Do you know what kind of matrix I have. Is it banded? As far as I can tell banded is all along the diagonal but I have basically a band of block matrices along the diagonal and another band (and it's symmetric partner) away from the diagonal along along with a few "random" (they are not random to me but look that way) blocks which are not in a band. Does this structure have a name associated with it? – Will

@BaummitAugen, I was thinking I could do factorization in two steps. In the first step I solve the block matrix where each block matrix counts as 1. This is say a 3000x3000 sparse matrix instead of 300000x30000. This should produce a bunch of block matricies along the diagonal. Then I solve these dense matricies along the diagonal which should go quickly. I am not exactly sure how to got about it though. I should probably work through a low dimensional example of block matrix factorization. – Will

Tbh, no cool name jumps to my mind when looking at this, sorry. Your idea sounds reasonable though, maybe you can employ some ideas from FEM/FDM? Iirc (lecture was a couple of years ago), the Schwarz methods yielded O(n) solvers for those systems, and from what I can see, yours looks kind of similar to those (esp. FEM). – Dorey

If your system comes from some grid-based stuff, Multi-Level approaches may also be useful (solve small system well, correct error on big system, rinse and repeat to convergence). Though in my experience so far CG with a great preconditioner beats ML, but I worked on a fairly narrow family of systems so far. CG also has the advantage that it is easy to implement, so you can just try your way through some PCs and see what works if you have no theory. It's also trivial to parallelize (hope that's a word). – Dorey

Here's a Java sparse matrix solver library: la4j.org You said C++, but perhaps this will be a direction. – Lib

There is a start in file unsupported / Eigen / src / SparseExtra / BlockSparseMatrix.h, not sure it still compile, but it used to work with ConjugateGradient<>. Let us (i.e., Eigen's developers) known if you make any progress. – Prather

@BaummitAugen, thank you for your many helpuful comments. We will look more into the precondition. CG seems to be the way to go. I agree it seems simple to implement. However, you said it is trivial to parallelize. Why is this? I don't see how you can parallelize it over iterations. The only opportunity I see is to parallelize the matrix*vector operations. For dense matrices that's memory bandwidth bound but maybe it works better with sparse matrices. – Will

@duffymo, our project is actually developed in Java. We used the CERN colt library which turns out not to be very good. We probably would have used la4j if we it existed when we started this project. In any case I don't think it will be ideal for our case but it's worth looking into. Thanks. I use JNI, C++, and Eigen for more critical stuff in Java but that's a bit of a pain, for multiple reasons, so a pure Java solution would be ideal. – Will

@Zboson With the sparse stuff I did, OMP loops for the multiplication did help. As it's easy, one might just try it. – Dorey

@BaummitAugen, that's basically what my colleague did in Java. I mean he did work sharing over the block matrix * vector. Okay, I think I have enough information now to put something together. – Will

Don't implement good libraries yourself. You can use SuiteSparse: [faculty.cse.tamu.edu/davis/suitesparse.html] or other packages. Anyway, I don't recommend factorization other than Cholesky. You can use CHOLMOD inside package – Psycholinguistics

@Aznaveh, but that's exactly what I did, implement my own solution. I used a custom conjugate gradient method, I used an incomplete Cholesky factorization as a preconditioner. I solved the incomplete Cholesky using my own custom code as well. I also used my own packing method. I ended up not even using Eigen because it is not really prepared for this case. The end result was about 4-5 times faster. I meant to write up our solution for SO. Maybe I will do that soon. – Will

As the matrix seems rather sparse, what about using block jordan decomposition and working on smaller submatrices? I guess LAPACK or openCV offer all you need, MKL/ IPP might also be of help... However, automatically finding submatrices for rather arbitrary large matrices is not that trivial either. – Hearne

Answer 1

check out SuiteSparse, http://faculty.cse.tamu.edu/davis/suitesparse.html The author, Tim Davis, is famous in the field of sparse matrices. He also received an award from Google for code quality. Performance of his code is also outstanding.

Cheers

Felodese

Answer 2

I think that ARPACK was designed to be efficient for tasks as find the solution of a system of equations Ax=b when A is sparce, as in your case. You can find the source code for ARPACK here.

Chatoyant