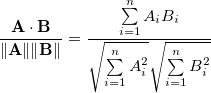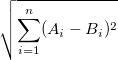Why does word2Vec use cosine similarity?

Question

I have been reading the papers on Word2Vec (e.g. this one), and I think I understand training the vectors to maximize the probability of other words found in the same contexts.

However, I do not understand why cosine is the correct measure of word similarity. Cosine similarity says that two vectors point in the same direction, but they could have different magnitudes.

For example, cosine similarity makes sense comparing bag-of-words for documents. Two documents might be of different length, but have similar distributions of words.

Why not, say, Euclidean distance?

Can anyone one explain why cosine similarity works for word2Vec?

Reptant

Many thanks Aaron and Martin. I guess I am confused by the statement "similar words end up near each other". I can see why backpropagating similar values would generate similar contexts, and therefore words that appear in similar contexts should produce similar values. However, I don't see why values that point in the same direction should generate the same contexts. But according to Aaron's link, I guess they do. Maybe the constant scale applied equally to all dimensions somehow cancels out. – Reptant

Answer 1

Cosine similarity of two n-dimensional vectors A and B is defined as:

which simply is the cosine of the angle between A and B.

while the Euclidean distance is defined as

Now think about the distance of two random elements of the vector space. For the cosine distance, the maximum distance is 1 as the range of cos is [-1, 1].

However, for the euclidean distance this can be any non-negative value.

When the dimension n gets bigger, two randomly chosen points have a cosine distance which gets closer and closer to 90°, whereas points in the unit-cube of R^n have an euclidean distance of roughly 0.41 (n)^0.5 (source)

TL;DR

cosine distance is better for vectors in a high-dimensional space because of the curse of dimensionality. (I'm not absolutely sure about it, though)

Sag

Sorry, I think this is not right. The curse of dimensionality applies equally well to cosine distance as it does to euclidean distance. – Ox

@Ox Could you elaborate on why you think this? (I'll check the average cosine distance of points in the n-dimensional hypercube with rising n when I have time ... if this goes to 0, then you might be right) – Sag

Related answer about curse of dimensionality which I found interesting: datascience.stackexchange.com/a/43709/132027 – Catacomb

Answer 2

Those two distance metrics are probably strongly correlated so it might not matter all that much which one you use. As you point out, cosine distance means we don't have to worry about the length of the vectors at all.

This paper indicates that there is a relationship between the frequency of the word and the length of the word2vec vector. http://arxiv.org/pdf/1508.02297v1.pdf

Ox