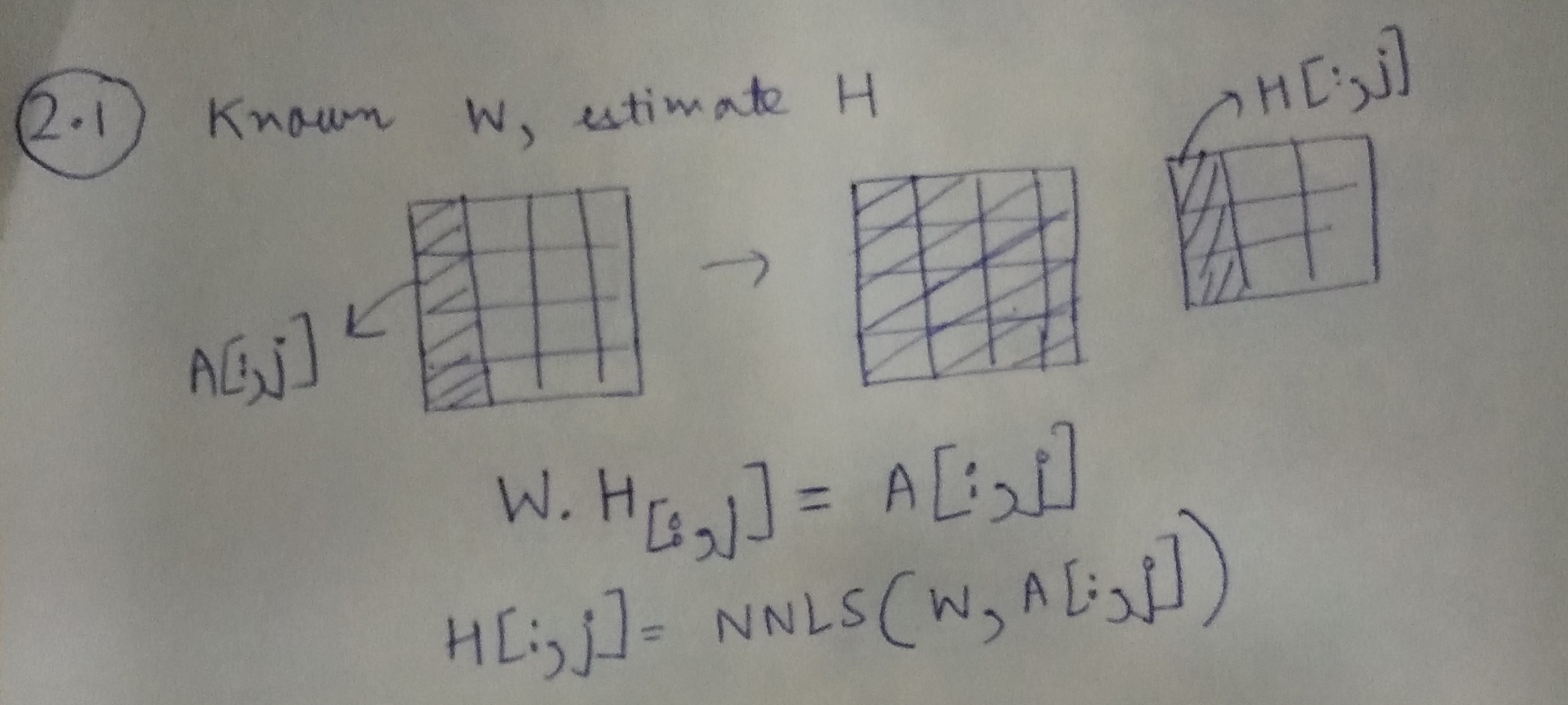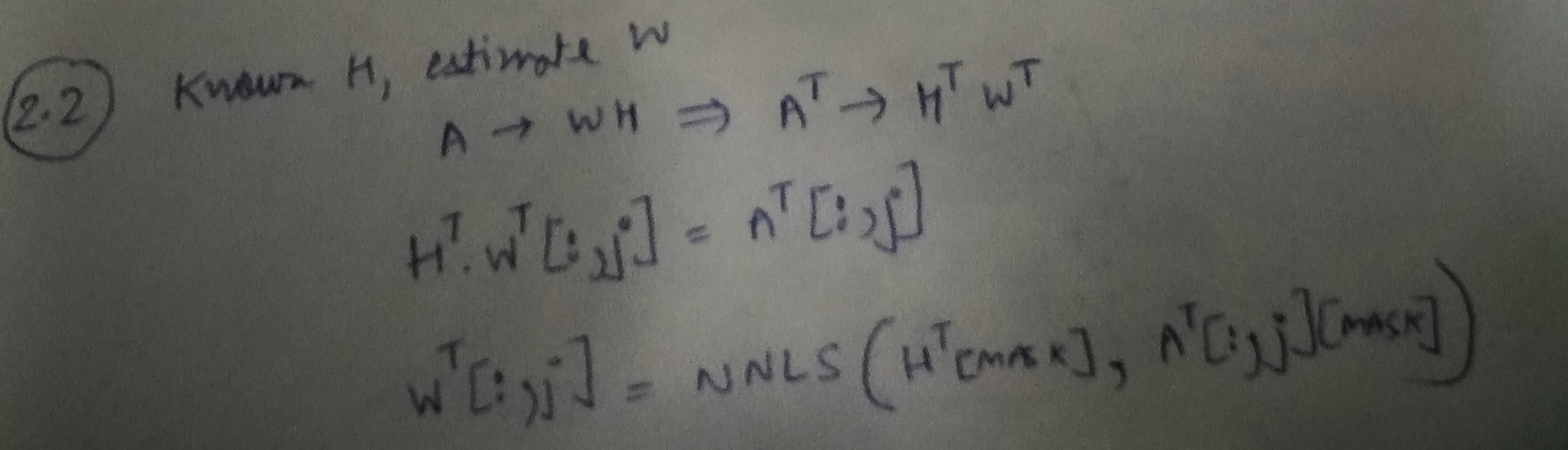Python Non negative Matrix Factorization that handles both zeros and missing data?

Question

I look for a NMF implementation that has a python interface, and handles both missing data and zeros.

I don't want to impute my missing values before starting the factorization, I want them to be ignored in the minimized function.

It seems that neither scikit-learn, nor nimfa, nor graphlab, nor mahout propose such an option.

Thanks!

Lloyd

Have you tried the implementation in scikit learn already? What problems does it give you? scikit-learn.org/stable/modules/generated/… – Aveyron

I mean, do you have problems because of imputing the missing values? why you would not want to do it is beyond my understanding. In general, if you do not impute missing values, then the vector is not valid and must be discarded from the computation. – Aveyron

Let's take the classic example of user x movies ratings matrix. For sure, the users will have rated only a small percentage of the movies, so there is a lot of missing values in the input matrix X. So what you want to do, is to guess the matrix factors (WH = X) by factorizing the matrix only from the available ratings, and then estimate the missing ones with the W and H you obtained. But I found a way of adding this to the current projected gradient implementation of scikit-learn, I will propose a pull request soon. – Generalist

Here is a very good explanation of this for general matrix factorization (without the non negativity constraint): quuxlabs.com/blog/2010/09/… – Generalist

Very nice write up, thanks. It's not python, but there is a toolbox for Matlab with all the bells and whistles: sites.google.com/site/nmftool – Aveyron

Yep I know it, and it actually has what I need through their weighted NMF, thanks. But I can't find a way to modify the existing implem in scikit-learn that scales well... I think I will have a look at how it's done in this toolbox – Generalist

Answer 1

Using this Matlab to python code conversion sheet I was able to rewrite NMF from Matlab toolbox library.
I had to decompose a 40k X 1k matrix with sparsity of 0.7%. Using 500 latent features my machine took 20 minutes for 100 iteration.

Here is the method:

import numpy as np
from scipy import linalg
from numpy import dot

def nmf(X, latent_features, max_iter=100, error_limit=1e-6, fit_error_limit=1e-6):
    """
    Decompose X to A*Y
    """
    eps = 1e-5
    print 'Starting NMF decomposition with {} latent features and {} iterations.'.format(latent_features, max_iter)
    X = X.toarray()  # I am passing in a scipy sparse matrix

    # mask
    mask = np.sign(X)

    # initial matrices. A is random [0,1] and Y is A\X.
    rows, columns = X.shape
    A = np.random.rand(rows, latent_features)
    A = np.maximum(A, eps)

    Y = linalg.lstsq(A, X)[0]
    Y = np.maximum(Y, eps)

    masked_X = mask * X
    X_est_prev = dot(A, Y)
    for i in range(1, max_iter + 1):
        # ===== updates =====
        # Matlab: A=A.*(((W.*X)*Y')./((W.*(A*Y))*Y'));
        top = dot(masked_X, Y.T)
        bottom = (dot((mask * dot(A, Y)), Y.T)) + eps
        A *= top / bottom

        A = np.maximum(A, eps)
        # print 'A',  np.round(A, 2)

        # Matlab: Y=Y.*((A'*(W.*X))./(A'*(W.*(A*Y))));
        top = dot(A.T, masked_X)
        bottom = dot(A.T, mask * dot(A, Y)) + eps
        Y *= top / bottom
        Y = np.maximum(Y, eps)
        # print 'Y', np.round(Y, 2)


        # ==== evaluation ====
        if i % 5 == 0 or i == 1 or i == max_iter:
            print 'Iteration {}:'.format(i),
            X_est = dot(A, Y)
            err = mask * (X_est_prev - X_est)
            fit_residual = np.sqrt(np.sum(err ** 2))
            X_est_prev = X_est

            curRes = linalg.norm(mask * (X - X_est), ord='fro')
            print 'fit residual', np.round(fit_residual, 4),
            print 'total residual', np.round(curRes, 4)
            if curRes < error_limit or fit_residual < fit_error_limit:
                break

return A, Y

Here I was using Scipy sparse matrix as input and missing values were converted to 0 using toarray() method. Therefore, the mask was created using numpy.sign() function. However, if you have nan values you could get same results by using numpy.isnan() function.

Brogdon

Cool =), thanks! Yes this is the downside of using a Multiplicative Update based implementation, it is quite slow compared to ALS or Projected Gradient. This is mainly due to the "dot(A, Y)" product, and adding missing values support to Projected Gradient (scikit-learn) introduces this product, and terribly slows down the computation, this is why I didn't send a pull request. Stochastic Gradient Descent allows the support of missing values easily and without overhead, but I find it quite slow too. I'm currently trying to do it using Alternating Least Squares (ALS), I'll post it when it's done. – Generalist

Oh I just noticed a bug in the initialization of the Y matrix (that is also present in the original matlab code): the least square initialization of Y uses the non masked X. This yields a bias toward estimating missing values as zeros in the initial A and Y (and matrix factorization algorithms are known to be sensitive to initialization). Solutions are: initializing Y randomly too, or ignoring the missing values in the least squares, i.e.: bool_mask = mask.astype(bool); for i in range(columns): Y[:,i] = linalg.lstsq(A[bool_mask[:,i],:], X[bool_mask[:,i],i])[0] – Generalist

@ThéoT Did you mange to find/implement the solution that scales well? I am currently using the above Multiplicative Update algorithm, but I am looking for faster NMF. – Zadazadack

In the end, I think it's not possible to do it efficiently with ALS either: let's say we want to compute updates of Y, the solution is (A^T.A)^-1 .A^T .X . The inverse of (A^T .A) (or the LU/Cholesky decomposition) will be different for each column of Y depending on the present values in the corresponding column of X, thus making it too slow. I did not needed the non negativity constraint anymore, so I went SGD, by sampling only the present values, and using the right tricks: batching, a good learning rate policy such as Adagrad, and early stopping (on a validation set). And L2 reg for sure. – Generalist

So maybe doing the same thing (Stochastic Gradient Descent) by enforcing the non negativity constraint might work, i.e by replacing all negative values in the embeddings (A and Y here) by zeros after each gradient step. But I'm not sure about convergence when combining stochastic and proximal (i.e. projected (i.e. thresholding A and Y values at zero (yeah fancy words uh))) gradient descent, but definitely might be worth trying :) – Generalist

Answer 2

Scipy has a method to solve non-negative least squares problem (NNLS). In this answer, I am reproducing my blogpost on using scipy's NNLS for non-negative matrix factorisation. You may also be interested in my other blog posts that use autograd, Tensorflow and CVXPY for NNMF.

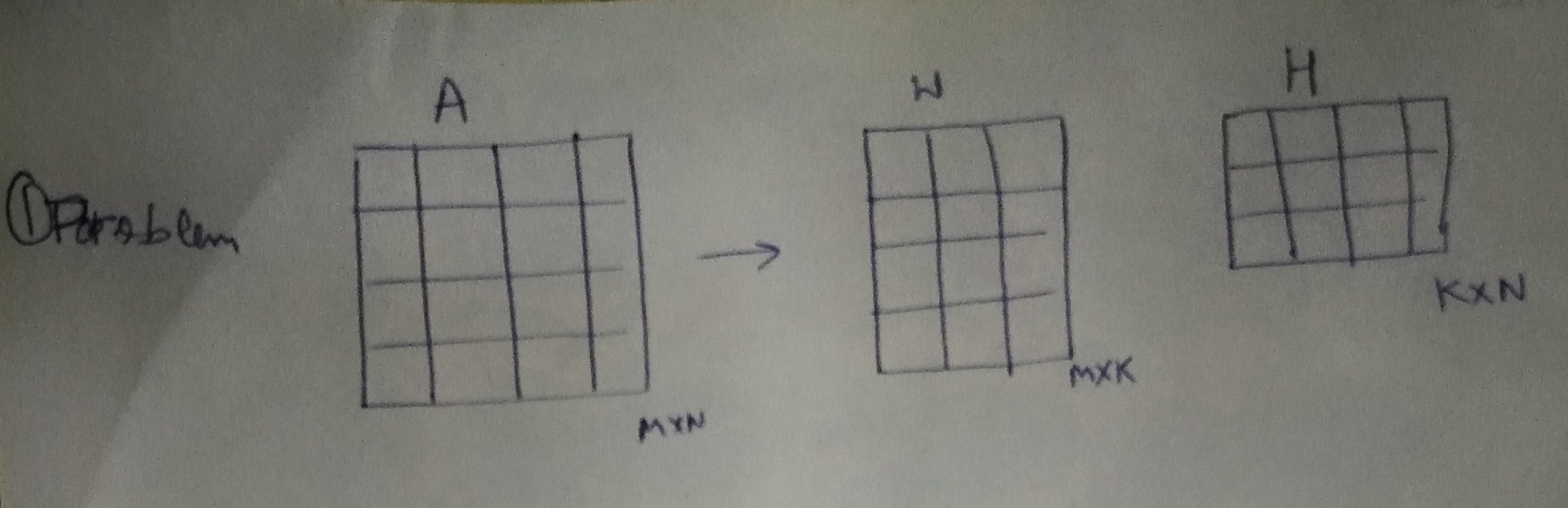
Goal: Our goal is given a matrix A, decompose it into two non-negative factors, as follows:

A (M×N) ≈ W (M×K) × H (K×N), such that  W (M×K) ≥ 0 and  H (K×N) ≥ 0 

Overview

Our solution consists of two steps. First, we fix W and learn H, given A. Next, we fix H and learn W, given A. We repeat this procedure iteratively. Fixing one variable and learning the other (in this setting) is popularly known as alternating least squares, as the problem is reduced to a least squares problem. However, an important thing to note is that since we want to constraint W and H to be non-negative, we us NNLS instead of least squares.

Step 1: Learning H, given A and W

Using the illustration above, we can learn each column of H, using the corresponding column from A and the matrix W.

H[:,j]=NNLS(W,A[:,j])

Handling missing entries in A

In the problem of collaborative filtering, A is usually the user-item matrix and it has a lot of missing entries. These missing entries correspond to user who have not rated items. We can modify our formulation to account for these missing entries. Consider that M' ≤ M entries in A have observed data, we would now modify the above equation as:

H[:,j]=NNLS(W[mask],A[:,j][mask])

where, the mask is found by considering only the M′ entries.

Step 2: Learning W, given A and H

Code example

Imports

import numpy as np
import pandas as pd

Creating matrix to be factorised

M, N = 20, 10

np.random.seed(0)
A_orig = np.abs(np.random.uniform(low=0.0, high=1.0, size=(M,N)))
print pd.DataFrame(A_orig).head()


0   1   2   3   4   5   6   7   8   9
0   0.548814    0.715189    0.602763    0.544883    0.423655    0.645894    0.437587    0.891773    0.963663    0.383442
1   0.791725    0.528895    0.568045    0.925597    0.071036    0.087129    0.020218    0.832620    0.778157    0.870012
2   0.978618    0.799159    0.461479    0.780529    0.118274    0.639921    0.143353    0.944669    0.521848    0.414662
3   0.264556    0.774234    0.456150    0.568434    0.018790    0.617635    0.612096    0.616934    0.943748    0.681820
4   0.359508    0.437032    0.697631    0.060225    0.666767    0.670638    0.210383    0.128926    0.315428    0.363711

Masking a few entries

A = A_orig.copy()
A[0, 0] = np.NAN
A[3, 1] = np.NAN
A[6, 3] = np.NAN

A_df = pd.DataFrame(A)
print A_df.head()


0   1   2   3   4   5   6   7   8   9
0   NaN 0.715189    0.602763    0.544883    0.423655    0.645894    0.437587    0.891773    0.963663    0.383442
1   0.791725    0.528895    0.568045    0.925597    0.071036    0.087129    0.020218    0.832620    0.778157    0.870012
2   0.978618    0.799159    0.461479    0.780529    0.118274    0.639921    0.143353    0.944669    0.521848    0.414662
3   0.264556    NaN 0.456150    0.568434    0.018790    0.617635    0.612096    0.616934    0.943748    0.681820
4   0.359508    0.437032    0.697631    0.060225    0.666767    0.670638    0.210383    0.128926    0.315428    0.363711

Defining matrices W and H

K = 4
W = np.abs(np.random.uniform(low=0, high=1, size=(M, K)))
H = np.abs(np.random.uniform(low=0, high=1, size=(K, N)))
W = np.divide(W, K*W.max())
H = np.divide(H, K*H.max())

pd.DataFrame(W).head()

0   1   2   3
0   0.078709    0.175784    0.095359    0.045339
1   0.006230    0.016976    0.171505    0.114531
2   0.135453    0.226355    0.250000    0.054753
3   0.167387    0.066473    0.005213    0.191444
4   0.080785    0.096801    0.148514    0.209789

pd.DataFrame(H).head()

0   1   2   3   4   5   6   7   8   9
0   0.074611    0.216164    0.157328    0.003370    0.088415    0.037721    0.250000    0.121806    0.126649    0.162827
1   0.093851    0.034858    0.209333    0.048340    0.130195    0.057117    0.024914    0.219537    0.247731    0.244654
2   0.230833    0.197093    0.084828    0.020651    0.103694    0.059133    0.033735    0.013604    0.184756    0.002910
3   0.196210    0.037417    0.020248    0.022815    0.171121    0.062477    0.107081    0.141921    0.219119    0.185125

Defining the cost that we want to minimise

def cost(A, W, H):
    from numpy import linalg
    WH = np.dot(W, H)
    A_WH = A-WH
    return linalg.norm(A_WH, 'fro')

However, since A has missing entries, we have to define the cost in terms of the entries present in A

def cost(A, W, H):
    from numpy import linalg
    mask = pd.DataFrame(A).notnull().values
    WH = np.dot(W, H)
    WH_mask = WH[mask]
    A_mask = A[mask]
    A_WH_mask = A_mask-WH_mask
    # Since now A_WH_mask is a vector, we use L2 instead of Frobenius norm for matrix
    return linalg.norm(A_WH_mask, 2)

Let us just try to see the cost of the initial set of values of W and H we randomly assigned.

cost(A, W, H)

7.3719938519859509

Alternating NNLS procedure

num_iter = 1000
num_display_cost = max(int(num_iter/10), 1)
from scipy.optimize import nnls

for i in range(num_iter):
    if i%2 ==0:
        # Learn H, given A and W
        for j in range(N):
            mask_rows = pd.Series(A[:,j]).notnull()
            H[:,j] = nnls(W[mask_rows], A[:,j][mask_rows])[0]
    else:
        for j in range(M):
            mask_rows = pd.Series(A[j,:]).notnull()
            W[j,:] = nnls(H.transpose()[mask_rows], A[j,:][mask_rows])[0]
    WH = np.dot(W, H)
    c = cost(A, W, H)
    if i%num_display_cost==0:
        print i, c

0 4.03939072472
100 2.38059096458
200 2.35814781954
300 2.35717011529
400 2.35711130357
500 2.3571079918
600 2.35710729854
700 2.35710713129
800 2.35710709085
900 2.35710708109



A_pred = pd.DataFrame(np.dot(W, H))
A_pred.head()

0   1   2   3   4   5   6   7   8   9
0   0.564235    0.677712    0.558999    0.631337    0.536069    0.621925    0.629133    0.656010    0.839802    0.545072
1   0.788734    0.539729    0.517534    1.041272    0.119894    0.448402    0.172808    0.658696    0.493093    0.825311
2   0.749886    0.575154    0.558981    0.931156    0.270149    0.502035    0.287008    0.656178    0.588916    0.741519
3   0.377419    0.743081    0.370408    0.637094    0.071684    0.529433    0.767696    0.628507    0.832910    0.605742
4   0.458661    0.327143    0.610012    0.233134    0.685559    0.377750    0.281483    0.269960    0.468756    0.114950

Let's view the values of the masked entries.

A_pred.values[~pd.DataFrame(A).notnull().values]

array([ 0.56423481,  0.74308143,  0.10283106])

Original values were:

A_orig[~pd.DataFrame(A).notnull().values]

array([ 0.5488135 ,  0.77423369,  0.13818295])

Azedarach

Answer 3

Down there is a decently fast and simple solution based on gradient descent with a quasi newton method:

import numpy.random as rd
from autograd_minimize import minimize
import numpy as np
import tensorflow as tf


def low_rank_matrix_factorization(X: np.array, rank: int = 5, l2_reg: float = 0.,
                                  positive: bool = False, opt_kwargs:
                                  dict = {'method': 'L-BFGS-B', 'tol': 1e-12}) -> np.array:
    """Factorises a matrix X into the product of two matrices. 
    The matrix can have nans.

    :param X: Input matrix
    :type X: np.array
    :param rank: rank of matrix decomposition, defaults to 5
    :type rank: int, optional
    :param l2_reg: l2 regularisation for the submatrices, defaults to 0.
    :type l2_reg: float, optional
    :param positive: if true, the matrices must have positive coefficients, defaults to False
    :type positive: bool, optional
    :param opt_kwargs: parameters for the optimizer, defaults to {'method': 'L-BFGS-B', 'tol': 1e-12}
    :type opt_kwargs: dict, optional
    :return: completed matrix
    :rtype: np.array
    """
    mask = tf.constant(~np.isnan(X), dtype=tf.float32)

    X_ = np.nan_to_num(X.copy(), 0)

    X_t = tf.constant(X_, dtype=tf.float32)

    Npos = tf.reduce_sum(mask)
    
    def model(U=None, V=None):
        return tf.reduce_sum(((U @ V) - X_t)**2 * mask)/Npos + (tf.reduce_mean(U**2) + tf.reduce_mean(V**2)) * l2_reg

    x0 = {'U': rd.random((X_t.shape[0], rank)),
          'V': rd.random((rank, X_t.shape[1]))}

    if positive:
        opt_kwargs['bounds'] = {'U': (0, None), 'V': (0, None)}
    res = minimize(model, x0, **opt_kwargs, backend='tf')

    return np.where(np.isnan(X), res.x['U'] @ res.x['V'], X)

Orose