I'm trying to accurately express an SVG Path as a UIBezierPath however sadly the addArc on UIBezierPath does not account for ellipses, only circles (only 1 value for radius).
bezierPath.addArc(withCenter:CGPoint radius:CGFloat startAngle:CGFloat endAngle:CGFloat clockwise:Bool)
My thinking would be to break the arc into pieces as svg curves, but I'm not sure how to calculate it.
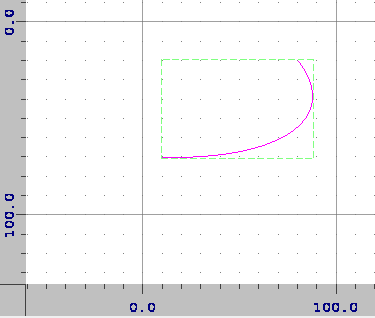
If I know the shape I want to make I can turn say, the top right corner arc
a150,150 0 1,0 150,-150 into a curve c82.84,0,150,44.77,150,100
but as I'll be parsing any possible arc, I need to know how to break up any ellipse and also calculate control points for each of the Bezier curves.
I've been looking at various resources that show cubic curves calculated in this way... http://www.spaceroots.org/documents/ellipse/node12.html
but I'm not sure how to express this in code
This is what I have so far....
Values for an a path in SVG
radiusX radiusY rotationOfArcX isLarge isSweep destinationX destinationY
Edit
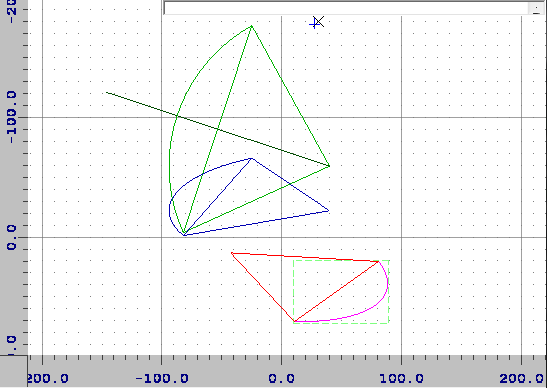
@Spektre your answer looks great when I render out some simple paths but the path is moving depending on large + sweep combination.
For example
Small Sweep / Large No Sweep
M 180.0 80.0 a50,50 0 0,1 50,50 z
M 180.0 80.0 a50,50 0 1,0 50,50 z
X has been translated +100
M 180.0 80.0
M 280.0 80.0
C 280.0 73.62 278.63 66.76 276.19 60.87
C 273.75 54.97 269.87 49.15 265.36 44.64
C 260.85 40.13 255.03 36.25 249.13 33.81
C 243.24 31.37 236.38 30.0 230.0 30.0
z
^^ small sweep example
Small No Sweep / Large Sweep
M 180.0 80.0 a50,50 0 0,0 50,50 z
M 180.0 80.0 a50,50 0 1,1 50,50 z
Y has been translated +100
M 180.0 80.0
M 180.0 180.0
C 186.38 180.0 193.24 178.63 199.13 176.19
C 205.03 173.75 210.85 169.87 215.36 165.36
C 219.87 160.85 223.75 155.03 226.19 149.13
C 228.63 143.24 230.0 136.38 230.0 130.0
C 230.0 123.62 228.63 116.76 226.19 110.87
C 223.75 104.97 219.87 99.15 215.36 94.64
C 210.85 90.13 205.03 86.25 199.13 83.81
C 193.24 81.37 186.38 80.0 180.0 80.0
C 173.62 80.0 166.76 81.37 160.87 83.81
C 154.97 86.25 149.15 90.13 144.64 94.64
C 140.13 99.15 136.25 104.97 133.81 110.87
C 131.37 116.76 130.0 123.62 130.0 130.0
z
^^ large sweep example
My codes version of your arc
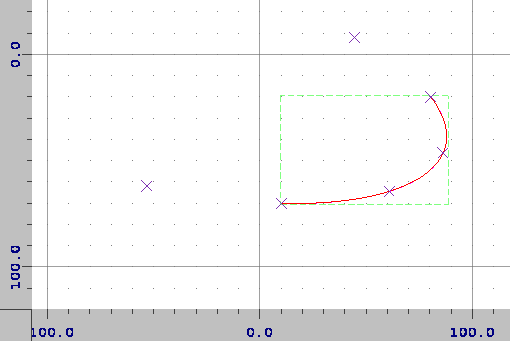
M 10 70 a 133.591805 50 12.97728 0 0 70 -50 z
M 10.0 70.0
M 65.33 62.67
C 53.75 67.15 35.85 69.91 17.44 70.06
C -0.97 70.2 -24.36 67.78 -45.14 63.57
C -65.92 59.36 -89.13 52.34 -107.24 44.79
z
My version of your code
private func arcAsCurves(x0: CGFloat, y0: CGFloat, a: CGFloat, b: CGFloat, angle: CGFloat, large: Bool, sweep: Bool, x1: CGFloat, y1: CGFloat) -> String {
//return "L\(x1) \(y1)"
var localSweep = sweep
if large { localSweep = !localSweep }
let pi = CGFloat.pi
let pi2 = pi*2
let ang = pi-(angle*pi/180.0) // [deg] -> [rad] and offset to match my coordinate system
let e = a/b
var c = cos(+ang)
var s = ang == pi ? 0.0 : sin(+ang)
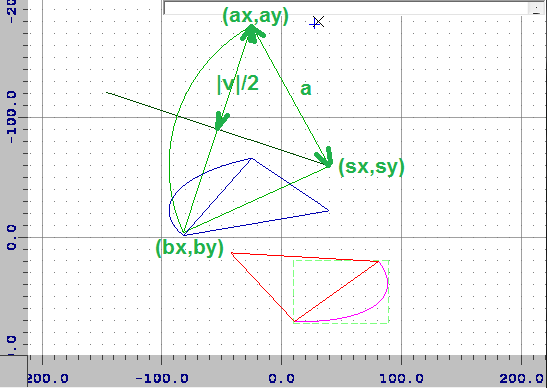
let ax = x0*c-y0*s // (ax,ay) = unrotated (x0,y0)
var ay = x0*s+y0*c
let bx = x1*c-y1*s // (bx,by) = unrotated (x1,y1)
var by = x1*s+y1*c
ay *= e // transform ellipse to circle by scaling y axis
by *= e
// rotated centre by angle
let axd = ax+bx
let ayd = ay+by
var sx = 0.5 * axd // mid point between A,B
var sy = 0.5 * ayd
var vx = ay-by // perpendicular direction vector to AB of size |AB|
var vy = bx-ax
var l = (a*a / (vx*vx + vy*vy)) - 0.25 // compute distance of center to (sx,sy) from pythagoras
//l=divide(a*a,(vx*vx)+(vy*vy))-0.25
if l < 0 { // handle if start/end points out of range (not on ellipse) center is in mid of the line
l = 0
}
l = sqrt(l)
vx *= l // rescale v to distance from id point to center
vy *= l
if localSweep { // pick the center side
sx += vx
sy += vy
} else {
sx -= vx
sy -= vy
}
// sx += localSweep ? vx : -vx
// sy += localSweep ? vy : -vy
var a0 = atan2(ax-sx, ay-sy) // compute unrotated angle range
var a1 = atan2(bx-sx, by-sy)
// a0 = atanxy(ax-sx,ay-sy);
// a1 = atanxy(bx-sx,by-sy);
ay /= e
by /= e
sy /= e // scale center back to ellipse
// pick angle range
var da = a1-a0
let zeroAng = 0.000001 * pi/180.0
if abs(abs(da)-pi) <= zeroAng { // half arc is without larc and sweep is not working instead change a0,a1
var db = (0.5 * (a0+a1)) - atan2(bx-ax,by-ay)
while (db < -pi) { db += pi2 } // db<0 CCW ... sweep=1
while (db > pi) { db -= pi2 } // db>0 CW ... sweep=0
if (db < 0.0 && !sweep) || (db > 0.0 && sweep) {
if da >= 0.0 { a1 -= pi2 }
if da < 0.0 { a0 -= pi2 }
}
}
else if large {
if da < pi && da >= 0.0 { a1 -= pi2 }
if da > -pi && da < 0.0 { a0 -= pi2 }
}
else {
if da > pi { a1 -= pi2 }
if da < -pi { a0 -= pi2 }
}
da = a1-a0
c = cos(-ang)
s = sin(-ang)
// var cx = sx*c-sy*s // don't need this
// var cy = sx*s+sy*c
var n: Int = 0
let maxCount: Int = 16
var dt: CGFloat = 0.0
var px = [CGFloat]()
var py = [CGFloat]()
n = Int(abs((CGFloat(maxCount) * da)/pi2))
if n < 1 { n = 1 }
else if n > maxCount { n = maxCount }
dt = da / CGFloat(n)
// get n+3 points on ellipse (with edges uniformly outside a0,a1)
let t = a0 - dt
for i in 0..<n+3 {
// point on axis aligned ellipse
let tt = t + (dt*CGFloat(i))
let xx = sx+a*cos(tt)
let yy = sy+b*sin(tt)
// rotate by ang
let c: CGFloat = cos(-ang)
let s: CGFloat = sin(-ang)
px.append(xx*c-yy*s)
py.append(xx*s+yy*c)
}
let m: CGFloat = 1/6
var string = ""
for i in 0..<n
{
// convert to interpolation cubic control points to BEZIER
let x0 = px[i+1]; let y0 = py[i+1];
let x1 = px[i+1]-(px[i+0]-px[i+2])*m; let y1 = py[i+1]-(py[i+0]-py[i+2])*m;
let x2 = px[i+2]+(px[i+1]-px[i+3])*m; let y2 = py[i+2]+(py[i+1]-py[i+3])*m;
let x3 = px[i+2]; let y3 = py[i+2];
if i == 0 {
let mString = String(format: "M%.2f %.2f", x0, y0)
string.append(mString)
}
let cString = String(format: "C%.2f %.2f %.2f %.2f %.2f %.2f", x1, y1, x2, y2, x3, y3)
string.append(cString)
}
return string
}