OK, encouraged by Allan that it wouldn't be that bad to draw the stuff myself, I decided also to have a go at attacking this problem. It is doing the thing I tried to avoid with this question but it might be helpful for the rest of you.
I took a slightly different approach, the main differences are that (1) we keep polylines instead of converting to polygons and (2) I'm not really comfortable with trigonometry so I used approxfun() instead to interpolate the lines and (3) we'll be working with absolute units instead of relative ones, so it won't be awkward when the device is resized.
First, as I intended to use this within custom geom functions, I aimed to make a grob structure that would be easy to paste at the end of a geom's draw methods. You can give it a grob, or the parameters for a grob. It changes the class of the grob, which will become relevant later, removes the linetype parameter and adds info for dashes and breaks.
library(grid)
library(scales)
linetypeGrob <- function(x, ..., dashes = 1, breaks = 1) {
if (!inherits(x, "polyline")) {
x <- polylineGrob(x, ...)
}
class(x)[[1]] <- "linetypeGrob"
x$gp$lty <- NULL
x$dashes <- dashes
x$breaks <- breaks
x
}
Now as I mentioned above, we'll come back to the class. The neat thing about custom grob classes, is that you can intercept them just before they are drawn so you can make last-minute changes. For this, we write an S3 method to the makeContext function in grid, that makes the relevant changes. I know it is a long function but I tried to make it easier to follow along by inserting comments that tell what I'm trying to do.
makeContext.linetypeGrob <- function(x) {
# Sort out line IDs
id <- x$id
if (is.null(id)) {
if (is.null(x$id.lengths)) {
id <- rep(1L, length(x$x))
} else {
id <- rep(seq_along(x$id.lengths), x$id.lengths)
}
}
# Delete previous line IDs
x$id <- NULL
x$id.lengths <- NULL
# Take dashes and breaks parameters out of the old grob
dashes <- x$dashes
x$dashes <- NULL
breaks <- x$breaks
x$breaks <- NULL
# Convert to absolute units
newx <- convertX(x$x, "mm", TRUE)
newy <- convertY(x$y, "mm", TRUE)
# Express lines as points along a cumulative distances
dist <- sqrt(diff(newx)^2 + diff(newy)^2)
cumdist <- cumsum(c(0, dist))
# Take new lines as a sequence along the cumulative distance
starts <- seq(0, max(cumdist), by = (dashes + breaks))
ends <- seq(dashes, max(cumdist), by = (dashes + breaks))
if (length(ends) == length(starts) - 1) {
# Case when the end actually should have gone beyond `max(cumdist)`
ends <- c(ends, max(cumdist))
}
# Set index for graphical parameters
gp_i <- findInterval(starts, cumdist[cumsum(rle(id)$lengths)]) + 1
# Basically dealing with elbow pieces a bit
# Find mismatches between the original segments that starts and ends fall on
start_id <- findInterval(starts, cumdist)
end_id <- findInterval(ends, cumdist)
mismatch <- which(start_id != end_id)
# Insert elbow pieces
starts <- c(starts, cumdist[end_id[mismatch]])
starts <- starts[{o <- order(starts)}] # Need the order for later
ends <- sort(c(ends, cumdist[end_id[mismatch]]))
# Join elbow pieces
new_id <- seq_along(start_id)
if (length(mismatch)) {
i <- rep_len(1, length(new_id))
i[mismatch] <- 2
new_id <- rep(new_id, i)
}
# Seperate lines with different IDs
keepfun <- approxfun(cumdist, id)
keep <- (keepfun(starts) %% 1) == 0 & (keepfun(ends) %% 1) == 0
# Interpolate x
xfun <- approxfun(cumdist, newx)
x0 <- xfun(starts[keep])
x1 <- xfun(ends[keep])
# Interpolate y
yfun <- approxfun(cumdist, newy)
y0 <- yfun(starts[keep])
y1 <- yfun(ends[keep])
# Expand graphic parameters by new ID
x$gp[] <- lapply(x$gp, function(x){
if (length(x) == 1) {
return(x)
} else {
x[as.integer(gp_i)]
}
})
# Put everything back into the grob
x$x <- unit(as.vector(rbind(x0, x1)), "mm")
x$y <- unit(as.vector(rbind(y0, y1)), "mm")
x$id <- as.vector(rbind(new_id[keep], new_id[keep]))
class(x)[[1]] <- "polyline"
x
}
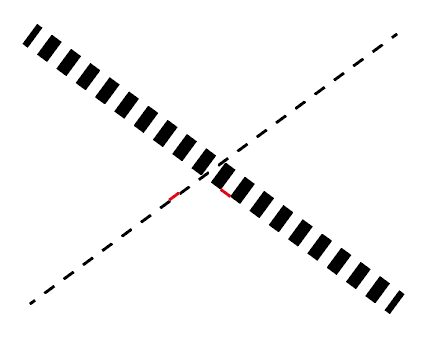
Lastly, to demonstrate that it works I'll draw some dummy data with this new grob. You could potentially use this like you would draw a normal polyline grob.
set.seed(100)
x <- c(cumsum(rnorm(10)), cumsum(rnorm(10)))
y <- c(cumsum(rnorm(10)), cumsum(rnorm(10)))
id <- rep(c(1, 2), each = 10)
gp <- gpar(lwd = c(2, 10), lineend = "butt",
col = c("magenta", "blue"))
grob <- linetypeGrob(scales::rescale(x),
scales::rescale(y),
id = id, gp = gp, dashes = 5, breaks = 2)
grid.newpage(); grid.draw(grob)
![enter image description here]()
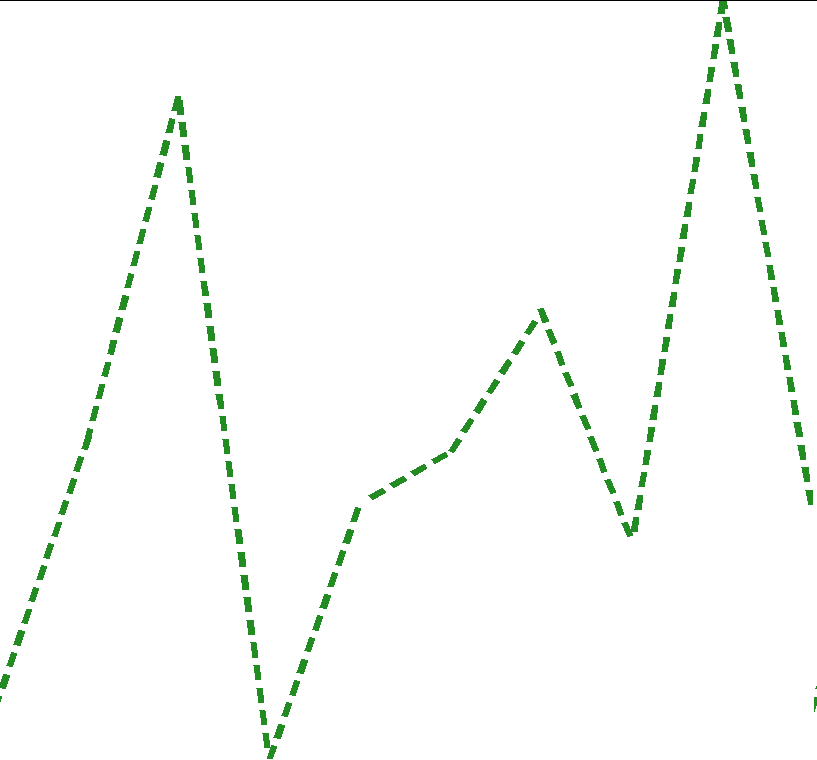
You can see that the lengths of the dashes and breaks remain equal if I resize the device:
![enter image description here]()