I happened to find (my) solution online as open source (image-quality-and-characterization-utilities, from include/Teisko/Image/Algorithm.hpp
The algorithm finds the Kth element of any set of size M<=64 in N steps, where N is the number of bits in the elements.
This is a radix-2 sort algorithm, which needs the original bit pattern int16_t data[7][7]; to be transposed into N planes of uint64_t bits[N] (10 for 10-bit images), with the MSB first.
// Runs N iterations for pixel data as bit planes in `bits`
// to recover the K(th) largest item (as set by initial threshold)
// The parameter `mask` must be initialized to contain a set bit for all those bits
// of interest in the corresponding pixel data bits[0..N-1]
template <int N> inline
uint64_t median8x8_iteration(uint64_t(&bits)[N], uint64_t mask, uint64_t threshold)
{
uint64_t result = 0;
int i = 0;
do
{
uint64_t ones = mask & bits[i];
uint64_t ones_size = popcount(ones);
uint64_t mask_size = popcount(mask);
auto zero_size = mask_size - ones_size;
int new_bit = 0;
if (zero_size < threshold)
{
new_bit = 1;
threshold -= zero_size;
mask = 0;
}
result = result * 2 + new_bit;
mask ^= ones;
} while (++i < N);
return result;
}
Use threshold = 25 to get median of 49 and mask = 0xfefefefefefefe00ull in the case the planes bits[] contain the support for 8x8 adjacent bits.
Toggling the MSB plane one can use the same inner loop for signed integers - and toggling conditionally MSB and the other planes one can use the algorithm for floating points as well.
Much after year 2016, Ice Lake with AVX-512 introduced _mm256_mask_popcnt_epi64 even on consumer machines, allowing the inner loop to be almost trivially vectorised for all the four submatrices in the common 8x8 support; the masks would be 0xfefefefefefefe00ull >> {0,1,8,9}.
The idea here is that the mask marks the set of pixels under inspection. Counting the number of ones (or zeros) in that set and comparing to a threshold, we can determine at each step if the Kth element belongs to the set of ones or zeros, producing also one correct output bit.
EDIT
Another method I tried was SSE2 version where one keeps a window of size Width*(7 + 1) sorted by rows:
original sorted
1 2 1 3 .... 1 1 0
2 1 3 4 .... 2 2 1
5 2 0 1 .... -> 5 2 3
. . . . .... . . .
Sorting 7 rows is efficiently done by a sorting network using 16 primitive sorting operations (32 instructions with 3-parameter VEX encoding + 14 instructions for memory access).
One can also incrementally remove element from input[row-1][column] from a presorted SSE2 register and add an element from input[row+7][column] to the register (which takes about 12 instructions per sorted column).
Having 7 sorted columns in 7 SSE2 registers, one can now implement bitonic merge sort of three different widths,
which at first column will sort in groups of
(r0),(r1,r2), ((r3,r4), (r5,r6))
<merge> <merge> <merge> // level #0
<--merge---> <---- merge* ----> // level #1
<----- merge + take middle ----> // partial level #2
At column 1, one needs to sort columns
(r1,r2), ((r3,r4),(r5,r6)), (r7)
******* **** <-- merge (r1,r2,r7)
<----- merge + take middle ----> <-- partial level #2
At column 2, with
r2, ((r3,r4),(r5,r6)), (r7,r8)
<merge> // level #0
** ******* // level #1
<----- merge + take middle ----> // level #2
This takes advantage of memorizing partially sorted substrings (and does it better than e.g. heap based priority queue). The final merging of the 3x7 and 4x7 element substrings does not need to compute every element correctly, since we are only interested in the element #24.
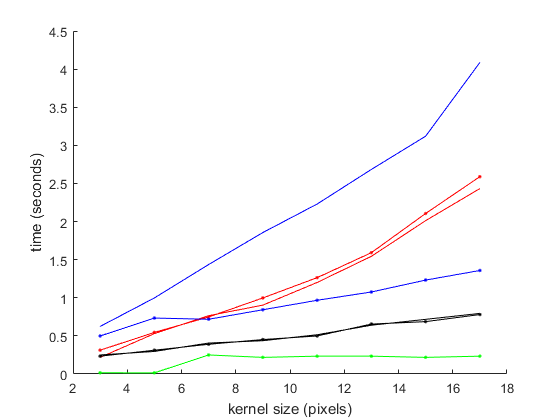
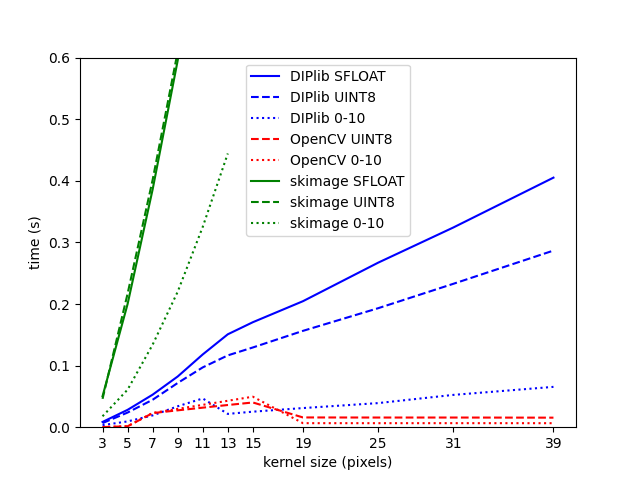
Still, while being better than (my implementations) of heap based priority queues and several hierarchical / flat histogram based methods, the overall winner was the popcount method (with a 64-bit popcount instruction).

SSEandAVXtags to your question. – Lumbye