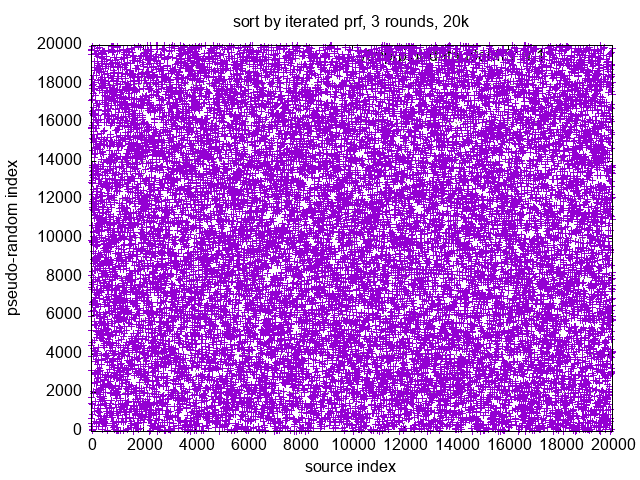
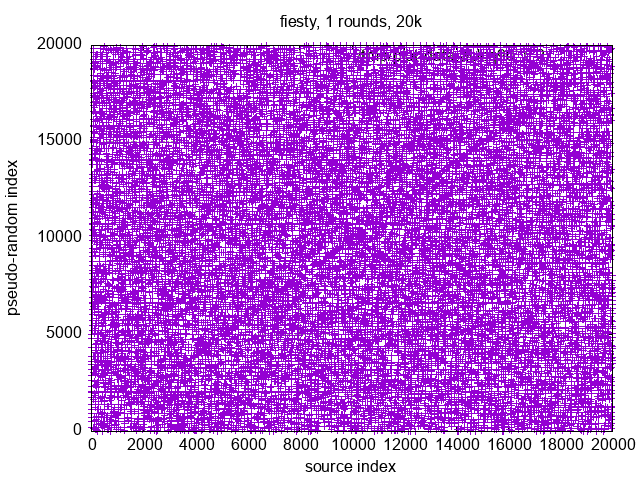
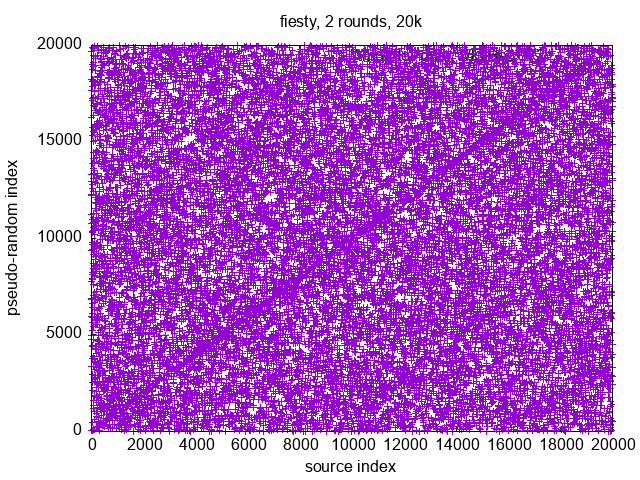
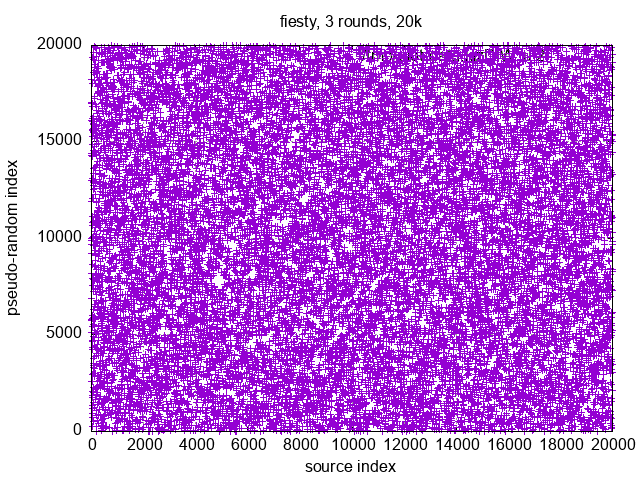
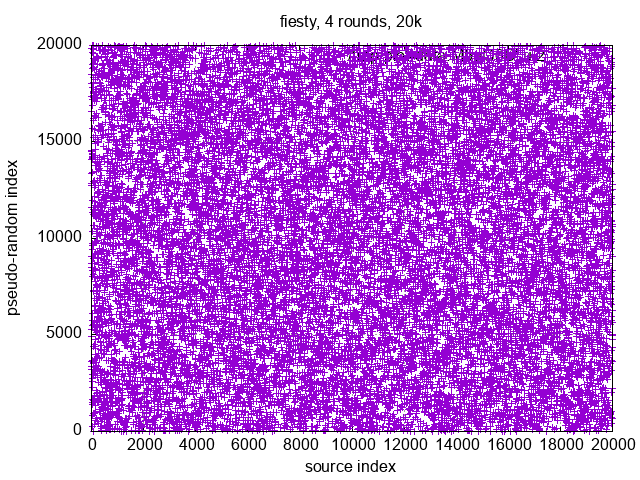
Given some interval [a, b] of indices (64-bit unsigned integers), I would like to quickly obtain an array that contains all of these indices ordered according to a uniformly distributed hash function, appearing random but actually being the same on every system, regardless of the used C++ implementation.
The goal is to find highly optimized such methods. You may use shared memory parallelism via Intel's oneTBB to improve performance.
Something like
vector<uint64_t> distributeIndices(uint64_t from, uint64_t to) {
unordered_set<uint64_t> uset;
for (uint64_t i = from; i <= to; i++)
uset.insert(i);
return vector<uint64_t>(uset.begin(), uset.end());
}
would generate desired results if unordered_set<uint64_t> would always use the same and a pseudo-randomly distributed hash function on every implementation, both of which is not the case. It would also be an inefficient solution. TBB equivalent:
tbb::concurrent_vector<uint64_t> distributeIndices(uint64_t from, uint64_t to) {
tbb::concurrent_unordered_set<uint64_t> uset;
tbb::parallel_for(from, to + 1, [&uset](uint64_t i) {
uset.insert(i);
}); // NOTE: This is only to illustrate a parallel loop, sequential insertion is actually faster.
return tbb::concurrent_vector<uint64_t>(uset.begin(), uset.end());
}
Note that distributeIndices(from, to) should return a random-looking permutation of {from, ..., to}.
Merely providing some hash functions is insufficient, and none of the answers at "Generating a deterministic int from another with no duplicates" actually answered that question.
Considertransformfrom this answer. Notably, a cyclic distribution is not a pseudo-random distribution:- Sorting {from, ..., to} w.r.t.
(uint64_t a, uint64_t b) { return transform(a) < transform(b) }distributeIndices(42, 42+99999999)[0, ..., 999]looks not random at all:
![stackoverflow.com/a/72188615 sorted]()
- Sorting {from, ..., to} w.r.t.
(uint64_t a, uint64_t b) { return transform(a) % n < transform(b) % n }distributeIndices(42, 42+99999999)[0, ..., 999]looks not random at all:
![stackoverflow.com/a/72188615 sorted modulo n]()
- Assigning each
xin {from, ..., to} totransform(x - from) % n + fromdistributeIndices(42, 42+99999999)happens to be bijective (since100000000and39293are coprime), butdistributeIndices(42, 42+99999999)[0, ..., 999]looks not random at all:![stackoverflow.com/a/72188615 assigned modulo n]()
distributeIndices(42, 42+3929299)is not bijective. It assigns only 100 different elements, cycling with a period of 100:
![stackoverflow.com/a/72188615 assigned modulo n]()
- Assigning each
xin {from, ..., to} totransform(x - from) + fromdistributeIndices(42, 42+99999999)is not bijective, e.g. it assigns3929375282657 > 42+99999999.
- Sorting {from, ..., to} w.r.t.
In particular, a linear congruential generator is not in general a bijection. But if you can make it such for each interval [from, to], while also hiding its cyclic nature, how?
Consequently, an answer should provide a specific hash function (and why it is fast and uniformly distributed), and how to efficiently utilize it in order to compute distributeIndices(from, to).
Again, it is crucial that distributeIndices(from, to) has the same result regardless of where it runs and what compiler it used, which must be guaranteed according to the C++ standard. But it is fine if for example distributeIndices(0,2) assigns a different index to 1 than distributeIndices(0,3) does.
Acceptable return types are std::vector, tbb::concurrent_vector, and dynamic arrays, consisting of elements of type uint64_t.
The function should perform well on ranges that include billions of indices.
[ In case you are curious on why this could be useful: Consider that there are different processes on different computing nodes, communicating via Message Passing Interface, and they should not send actual data (which is big), but only indices of data entries which they are processing. At the same time, the order to process data should be pseudo-randomized so that the progress speed is not "bouncing" much (which it does, when processing along the ordered indices). This is essential for reliable predictions of how long the overall computation will take. So every node must know which transformed index refers to which actual index, i.e. every node must compute the same result for distributeIndices(from, to). ]
The fastest correctly working solution wins the accepted answer.
- No C/C++ code, no acceptable answer.
(Except when it is a proof that the problem cannot be solved efficiently.)
I will test solutions with GCC 11.3 -O3 on my old i7-3610QM laptop with 8 hardware threads on 100 million indices (i.e. distributeIndices(c, c + 99999999)), and may change accepted answers when future answers provide a better performing solution.
Testing code (run up to 10 times, pick fastest execution):
int main(int argc, char* argv[]) {
uint64_t c = argc < 3 ? 42 : atoll(argv[1]);
uint64_t s = argc < 3 ? 99999 : atoll(argv[2]); // 99999999 for performance testing
for (unsigned i = 0; i < 10; i++) {
chrono::time_point<chrono::system_clock> startTime = chrono::system_clock::now();
auto indices = distributeIndices(c, c + s);
chrono::microseconds dur = chrono::duration_cast<chrono::microseconds>(chrono::system_clock::now() - startTime);
cout << durationStringMs(dur) << endl;
// [... some checks ...]
#if 0 // bijectivity check
set<uint64_t> m = set<uint64_t>(indices.begin(), indices.end());
cout << "min: " << *m.begin() << " , max: " << *prev(m.end()) << ", #elements: " << m.size() << endl;
#endif
cout << "required average: " << round((2.0L * c + s) / 2, 2) << endl;
long double avg = accumulate(indices.begin(), indices.end(), __uint128_t(0)) / static_cast<long double>(indices.size());
string sa = round(avg, 2);
cout << "actual average: " << sa << endl;
auto printTrendlineHelpers = [](uint64_t minX, string avgX, uint64_t maxX, uint64_t minY, string avgY, uint64_t maxY) {
cout << "Trendline helpers:" << endl;
cout << "[max] " << minX << " " << maxY << " " << avgX << " " << maxY << " " << maxX << " " << maxY << endl;
cout << "[avg] " << minX << " " << avgY << " " << avgX << " " << avgY << " " << maxX << " " << avgY << endl;
cout << "[min] " << minX << " " << minY << " " << avgX << " " << minY << " " << maxX << " " << minY << endl;
};
// Print some plottable data, for e.g. https://www.rapidtables.com/tools/scatter-plot.html
unsigned plotAmount = 2000;
auto printPlotData = [&](uint64_t start, uint64_t end) {
long double rng = static_cast<long double>(end - start);
long double avg = accumulate(indices.begin() + start, indices.begin() + end, __uint128_t(0)) / rng;
cout << "\ndistributeIndices(" << c << ", " << c << "+" << s << ")[" << start << ", ..., " << end - 1 << "]: (average " << round(avg, 2) << ")" << endl;
stringstream ss;
for (unsigned i = start; i < end; i++)
ss << i << " " << indices[i] << (i + 1 == end ? "" : " ");
cout << ss.str() << endl;
printTrendlineHelpers(start, round(start + rng / 2, 2), end - 1, c, sa, c + s);
};
printPlotData(0, plotAmount); // front
printPlotData(indices.size() / 2 - plotAmount / 2, indices.size() / 2 + plotAmount / 2); // middle
printPlotData(indices.size() - plotAmount, indices.size()); // back
#if 1 // Print average course
if (s >= 1000000)
plotAmount *= 10;
stringstream ss;
for (uint64_t start = 0; start < indices.size(); start += plotAmount) {
uint64_t end = min(start + plotAmount, indices.size());
uint64_t i = start + (end - start) / 2;
long double avg = accumulate(indices.begin() + start, indices.begin() + end, __uint128_t(0)) / static_cast<long double>(end - start);
ss << i << " " << round(avg, 2) << (end == indices.size() ? "" : " ");
}
cout << "\nAverage course of distributeIndices(" << c << ", " << c << "+" << s << ") with slices of size " << plotAmount << ":\n" << ss.str() << endl;
printTrendlineHelpers(c, sa, c + s, c, sa, c + s);
break;
#endif
}
return 0;
}
- Storage of the result (e.g. via static variables) is obviously not allowed.
uint64_t fromanduint64_t tocannot be consideredconstexpr.
My two (unsuitable) examples would be 14482.83 ms (14 s 482.83 ms) and 186812.68 ms (3 min 6 s 812.68 ms).
The second approach seems terribly slow, but upon closer inspection it is the only one that on my system actually distributes the values:
unordered_set<uint64_t>variant:
e.g. 100000041, 100000040, 100000039, 100000038, 100000037, ... // badtbb::concurrent_unordered_set<uint64_t>variant:
e.g. 67108864, 33554432, 16777216, 83886080, 50331648, ... // well-distributed, but not looking randomdistributeIndices(42, 42+99999999)[0, ..., 999]with polynomial trendline:
![https://mcmap.net/q/662367/-fastest-way-to-bring-a-range-from-to-of-64-bit-integers-into-pseudo-random-order-with-same-results-across-all-platforms example]()
The above distribution looks ordered, not random.
An exemplary distribution suggesting randomness can be obtained from olegarch's answer, as of Apr 30, 2023.
// LCG params from: https://nuclear.llnl.gov/CNP/rng/rngman/node4.html
std::vector<uint64_t> distributeIndices(uint64_t lo, uint64_t hi) {
uint64_t size = hi - lo + 1;
std::vector<uint64_t> vec(size);
for(uint64_t i = 0; i < size; i++)
vec[i] = i + lo;
uint64_t rnd = size ^ 0xBabeCafeFeedDad;
for(uint64_t i = 0; i < size; i++) {
rnd = rnd * 2862933555777941757ULL + 3037000493;
uint64_t j = rnd % size;
uint64_t tmp = vec[i]; vec[i] = vec[j]; vec[j] = tmp;
}
return std::move(vec);
}
Note that the solution is still incorrect since it doesn't provide uniform distributions for all ranges, as shown further below. It also does not utilize parallel computing, but it performs well: Computing 100 million indices took 3235.18 ms on my i7-3610QM.
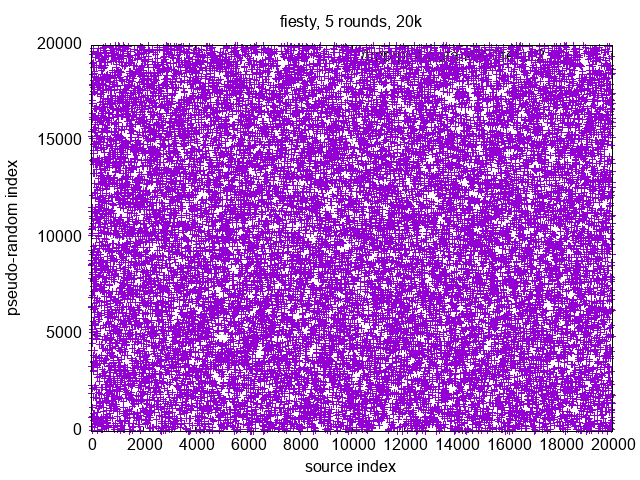
- front ;
distributeIndices(42, 42+99999999)[0, ..., 1999]with polynomial trendline:
![stackoverflow.com/a/76077930 front]()
- middle ;
distributeIndices(42, 42+99999999)[49999000, ..., 50000999]with polynomial trendline:
![stackoverflow.com/a/76077930 middle]()
- back ;
distributeIndices(42, 42+99999999)[99998000, ..., 99999999]with polynomial trendline:
![stackoverflow.com/a/76077930 back]()
The above distribution is looking random, even though the average seems to be a little low and bouncy in the beginning. Its global trend looks as follows. - average course of
distributeIndices(42, 42+99999999)with polynomial trendline:
![stackoverflow.com/a/76077930 averages]()
The polynomial trendline deviates up to 5% from the global average, so the distribution is not uniform.
And for some ranges, it gets worse: - average course of
distributeIndices(0, 67108863)with polynomial trendline:
![stackoverflow.com/a/76077930 another averages]()
- front ;
distributeIndices(0, 67108863)[0, ..., 1999]with polynomial trendline:
![stackoverflow.com/a/76077930 another front]()
This is clearly not an acceptable distribution.
An exemplary distribution with a flawless trendline can be obtained from Severin Pappadeux's answer, as of Apr 30, 2023. Following the suggestions, I added some parallelization.
uint64_t m = 0xd1342543de82ef95ULL; // taken from https://arxiv.org/pdf/2001.05304.pdf
uint64_t c = 0x1ULL;
inline auto lcg(uint64_t xi) -> uint64_t { // as LCG as it gets
return m*xi + c;
}
inline auto cmp_lcg(uint64_t a, uint64_t b) -> bool {
return lcg(a) < lcg(b);
}
auto distributeIndices(uint64_t from, uint64_t to) -> std::vector<uint64_t> {
uint64_t size = to - from + 1;
std::vector<uint64_t> z(size);
tbb::parallel_for(uint64_t(0), size, [&](uint64_t i) {
z[i] = from + i;
}); // instead of std::iota(z.begin(), z.end(), from);
tbb::parallel_sort(z.begin(), z.end(), cmp_lcg); // instead of std::sort(z.begin(), z.end(), cmp_lcg);
return z;
}
To give an idea of performance boost via multithreading, computing 100 million indices on my i7-3610QM took 15925.91 ms sequentially and 3666.21 ms with parallelization (on 8 hardware threads).
On a computing cluster with Intel Xeon Platinum 8160 processors, I measured the (#cpu,duration[ms]) results (1,19174.65), (2,9862.29), (4,5580.47), (8,3402.05), (12,2119.28), (24,1606.78), and (48,1330.20).
It should also be noted, that the code is better optimized and runs much faster, when turning cmp_lcg into a lambda function, e.g. auto cmp_lcg = [](uint64_t a, uint64_t b) -> bool { return lcg(a) < lcg(b); };. This way, it performed best at 2608.15 ms on my i7-3610QM. Slightly even better performance can be reached when declaring global variables m and c as constexpr, or making them local or literals, which led to a duration of 2542.14 ms.
- average course of
distributeIndices(42, 42+99999999)with polynomial trendline:
![stackoverflow.com/a/76082801 averages]()
![stackoverflow.com/a/76082801 averages zoomed]()
But when looking at the actual distribution, it becomes apparent that it is not random, but ordered: - front ;
distributeIndices(42, 42+99999999)[0, ..., 1999]with polynomial trendline:
![stackoverflow.com/a/76082801 front]()
The solution is incorrect regarding the task that distributions should appear to be random, but due to its mostly✻ nice distributions, it is particularly useful for the previously mentioned MPI use case. So if there won't be any fully correct solutions, it will make an accepted answer as well — so long as there won't be given any plausible ranges where it has non-uniform distributions. Plausible here means, that values where the algorithm would run for at least several days, can be ignored.
✻The factor 0xd1342543de82ef95 shows some weaknesses in the spectral test, and I haven't yet found a reason not to use 0x9e3779b97f4a7c15 instead.
After all this, it should be clear what it means that the task is to combine
- perceived randomness of a
- uniform bijective distribution of
- plausible arbitrary intervals, with
- high performance.
I am very curious if there even exist any correct and well-performing solutions to the problem!
A negative answer to this question, with a corresponding proof, would of course also be acceptable.
Even better than distributeIndices(uint64_t, uint64_t) -> vector<uint64_t> would be an approach to not have to create a vector, but merely iterating the indices in pseudo-random order, but that would require each pseudo-random index to be efficiently computable from its actual index (without iterating all the elements before it). I would be surprised it that is possible, but I'd gladly be surprised. Such approaches are always considered better than the vector-constructing ones, and are compared amongst each other by the duration of iterating 100 million indices.
