Voronoi - Compute exact boundaries of every region

Question

I'm trying to compute the exact boundaries of every region of a Voronoi Diagram using scipy.spatial.Voronoi, in the case that all the points are inside a pre-defined polygon. For example, using the example in this documentation.

what if I need to compute Voroni with the same points but inside a rectangle with the following boundaries

global_boundaries = np.array([[-2, -2], [4, -2], [4, 4], [-2, 4], [-2, -2]])

and I need to compute the precise boundaries of every Voronoi region, like that?

voronoi_region_1_boundaries = [[-2, -2], [0.5, -2], [0.5, 0.5], [-2, 0-5], [-2, -2]]
voronoi_region_2_boundaries = [[-2, 1.5], [0.5, 1.5], [0.5, 4], [-2, 4], [-2, 1.5]]
voronoi_region_3_boundaries = [[-2, 0.5], [0.5, 0.5], [0.5, 1.5], [-2, 1.5], [-2, 0.5]]

and so on for all the 9 regions, instead of

vor.regions 
[[], [-1, 0], [-1, 1], [1, -1, 0], [3, -1, 2], [-1, 3], [-1, 2], [3, 2, 0, 1], [2, -1, 0], [3, -1, 1]]

How do I compute the missing endpoint of an infinite ridge?

I've tried to adapt this code http://nbviewer.ipython.org/gist/pv/8037100

related to this problem Colorize Voronoi Diagram

but it's working only for rounded boundaries. I've modified it considering a radius such that my area is completely inside the circle, and then computing the intersection between the line connecting the points and the circumference and the boundaries. It works, but only for the first point and after that I have "GEOMETRYCOLLECTION EMPTY" as a result.

direction = np.sign(np.dot(midpoint - center, n)) * n
super_far_point = vor.vertices[v2] + direction * radius
line_0 = LineString([midpoint, super_far_point])
for i in range(0, len(map_boundaries)-1):
    i += 1
    line_i = LineString([(map_boundaries[i-1]), (map_boundaries[i])])
    if line_0.intersection(line_i) != 0:
        far_point = line_0.intersection(line_i)

new_region.append(len(new_vertices))
new_vertices.append(far_point.tolist())

Has anyone ever solved a similar problem?

Can anyone help?

Glyconeogenesis

Answer 1

1. Algorithm

I suggest the following two-step approach:

1. First, make a convex polygon for each of the Voronoi regions. In the case of the infinite regions, do this by splitting the point at infinity into two points that are far enough away, joined by an edge. ("Far enough away" means that the extra edge passes entirely outside the bounding polygon.)

2. Intersect each of the polygons from step (1) with the bounding polygon, using shapely's intersection method.

The benefit of this approach over Ophir Cami's answer is that it works with non-convex bounding polygons, and the code is a little simpler.

2. Example

Let's start with the Voronoi diagram for the points from Ophir Cami's answer. The infinite ridges are shown as dashed lines by scipy.spatial.voronoi_plot_2d:

Then for each Voronoi region we construct a convex polygon. This is easy for the finite regions, but we have to zoom out a long way to see what happens to the infinite Voronoi regions. The polygons corresponding to these regions have an extra edge that is far enough away that it lies entirely outside the bounding polygon:

Now we can intersect the polygons for each Voronoi region with the bounding polygon:

In this case, all the Voronoi polygons have non-empty intersection with the bounding polygon, but in the general case some of them might vanish.

3. Code

The first step is to generate polygons corresponding to the Voronoi regions. Like Ophir Cami, I derived this from the implementation of scipy.spatial.voronoi_plot_2d.

from collections import defaultdict

from shapely.geometry import Polygon

def voronoi_polygons(voronoi, diameter):
    """Generate shapely.geometry.Polygon objects corresponding to the
    regions of a scipy.spatial.Voronoi object, in the order of the
    input points. The polygons for the infinite regions are large
    enough that all points within a distance 'diameter' of a Voronoi
    vertex are contained in one of the infinite polygons.

    """
    centroid = voronoi.points.mean(axis=0)

    # Mapping from (input point index, Voronoi point index) to list of
    # unit vectors in the directions of the infinite ridges starting
    # at the Voronoi point and neighbouring the input point.
    ridge_direction = defaultdict(list)
    for (p, q), rv in zip(voronoi.ridge_points, voronoi.ridge_vertices):
        u, v = sorted(rv)
        if u == -1:
            # Infinite ridge starting at ridge point with index v,
            # equidistant from input points with indexes p and q.
            t = voronoi.points[q] - voronoi.points[p] # tangent
            n = np.array([-t[1], t[0]]) / np.linalg.norm(t) # normal
            midpoint = voronoi.points[[p, q]].mean(axis=0)
            direction = np.sign(np.dot(midpoint - centroid, n)) * n
            ridge_direction[p, v].append(direction)
            ridge_direction[q, v].append(direction)

    for i, r in enumerate(voronoi.point_region):
        region = voronoi.regions[r]
        if -1 not in region:
            # Finite region.
            yield Polygon(voronoi.vertices[region])
            continue
        # Infinite region.
        inf = region.index(-1)              # Index of vertex at infinity.
        j = region[(inf - 1) % len(region)] # Index of previous vertex.
        k = region[(inf + 1) % len(region)] # Index of next vertex.
        if j == k:
            # Region has one Voronoi vertex with two ridges.
            dir_j, dir_k = ridge_direction[i, j]
        else:
            # Region has two Voronoi vertices, each with one ridge.
            dir_j, = ridge_direction[i, j]
            dir_k, = ridge_direction[i, k]

        # Length of ridges needed for the extra edge to lie at least
        # 'diameter' away from all Voronoi vertices.
        length = 2 * diameter / np.linalg.norm(dir_j + dir_k)

        # Polygon consists of finite part plus an extra edge.
        finite_part = voronoi.vertices[region[inf + 1:] + region[:inf]]
        extra_edge = [voronoi.vertices[j] + dir_j * length,
                      voronoi.vertices[k] + dir_k * length]
        yield Polygon(np.concatenate((finite_part, extra_edge)))

The second step is to intersect the Voronoi polygons with the bounding polygon. We also need to choose an appropriate diameter to pass to voronoi_polygons.

import matplotlib.pyplot as plt
from scipy.spatial import Voronoi

points = np.array([[0.1, -0.4], [0, 1.5], [0, 2.25], [1, 0], [1, 1], [1, 2],
                   [2, 0], [2.5, 1], [2, 2], [2.3, 2.3], [-0.5, -1.3], [-1.5, 3]])
boundary = np.array([[-5, -2], [3.4, -2], [4.7, 4], [2.7, 5.7], [-1, 4]])

x, y = boundary.T
plt.xlim(round(x.min() - 1), round(x.max() + 1))
plt.ylim(round(y.min() - 1), round(y.max() + 1))
plt.plot(*points.T, 'b.')

diameter = np.linalg.norm(boundary.ptp(axis=0))
boundary_polygon = Polygon(boundary)
for p in voronoi_polygons(Voronoi(points), diameter):
    x, y = zip(*p.intersection(boundary_polygon).exterior.coords)
    plt.plot(x, y, 'r-')

plt.show()

This plots the last of the figures in §2 above.

Sullivan

I got the example working, but running with points = [[0, 6000042], [5, 6000060], [8, 6000076], [14, 6000016], [30, 6000069], [39, 6000000]]; boundary = [[-1, 5999999], [40, 5999999], [40, 6000077], [-1, 6000077], [-1, 5999999]] fails. It raises ValueError: need more than 0 values to unpack at dir_j, dir_k = ridge_direction[i, j]. Any idea why? Shifting the points & bounds towards origin with shift = points.min(axis=0); points -= shift; boundary -= shift does, however, make it work again. Why might this be? – Say

I am experiencing the same issue as @anttikoo, working with a lot of geographic coordinates (WGS84). Shifting the points does not help in my case. Neither does a coordinates reprojection in a local system (azimuthal equidistant projection). But still, the valid last ridge direction I proceed has an y value close to -1, I keep wondering if this is not causing an issue with the -1 infinite values : ridge_direction[i, j]=[array([-0.08074507, -0.99673479])] – Engross

Answer 2

I took the voronoi_plot_2d and modified it. see below.

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import Voronoi
from shapely.geometry import Polygon, Point

# Voronoi - Compute exact boundaries of every region


def angle_between(v0, v1):
    return np.math.atan2(np.linalg.det([v0, v1]), np.dot(v0, v1))


def calc_angle(c0, c1, c2):
    return angle_between(np.array(c1) - np.array(c0), np.array(c2) - np.array(c1))


def is_convex(polygon):
    temp_coords = np.array(polygon.exterior.coords)
    temp_coords = np.vstack([temp_coords, temp_coords[1, :]])

    for i, (c0, c1, c2) in enumerate(zip(temp_coords, temp_coords[1:], temp_coords[2:])):
        if i == 0:
            first_angle_crit = calc_angle(c0, c1, c2) > 0
        elif (calc_angle(c0, c1, c2) > 0) != first_angle_crit:
            return False
    return True


def infinite_segments(vor_):
    line_segments = []
    center = vor_.points.mean(axis=0)
    for pointidx, simplex in zip(vor_.ridge_points, vor_.ridge_vertices):
        simplex = np.asarray(simplex)
        if np.any(simplex < 0):
            i = simplex[simplex >= 0][0]  # finite end Voronoi vertex

            t = vor_.points[pointidx[1]] - vor_.points[pointidx[0]]  # tangent
            t /= np.linalg.norm(t)
            n = np.array([-t[1], t[0]])  # normal

            midpoint = vor_.points[pointidx].mean(axis=0)
            direction = np.sign(np.dot(midpoint - center, n)) * n

            line_segments.append([(vor_.vertices[i, 0], vor_.vertices[i, 1]),
                                  (direction[0], direction[1])])
    return line_segments


class NotConvexException(Exception):
    def __str__(self):
        return 'The Polygon is not Convex!!!'


class NotAllPointsAreInException(Exception):
    def __str__(self):
        return 'Not all points are in the polygon!!!'


def intersect(p0, u, q0, q1):
    v = (q1 - q0)[np.newaxis].T
    A = np.hstack([u, -v])
    b = q0 - p0
    try:
        inv_A = np.linalg.inv(A)
    except np.linalg.LinAlgError:
        return np.nan, np.nan
    return np.dot(inv_A, b)


def _adjust_bounds(ax__, points_):
    ptp_bound = points_.ptp(axis=0)
    ax__.set_xlim(points_[:, 0].min() - 0.1*ptp_bound[0], points_[:, 0].max() + 0.1*ptp_bound[0])
    ax__.set_ylim(points_[:, 1].min() - 0.1*ptp_bound[1], points_[:, 1].max() + 0.1*ptp_bound[1])


def in_polygon(polygon, points_):
    return [polygon.contains(Point(x)) for x in points_]


def voronoi_plot_2d_inside_convex_polygon(vor_, polygon, ax__=None, **kw):
    from matplotlib.collections import LineCollection

    if not all(in_polygon(polygon, vor_.points_)):
        raise NotAllPointsAreInException()

    if not is_convex(polygon):
        raise NotConvexException()

    if vor_.points.shape[1] != 2:
        raise ValueError("Voronoi diagram is not 2-D")

    vor_inside_ind = np.array([i for i, x in enumerate(vor_.vertices) if polygon.contains(Point(x))])
    vor_outside_ind = np.array([i for i, x in enumerate(vor_.vertices) if not polygon.contains(Point(x))])
    ax__.plot(vor_.points[:, 0], vor_.points[:, 1], '.')
    if kw.get('show_vertices', True):
        ax__.plot(vor_.vertices[vor_inside_ind, 0], vor_.vertices[vor_inside_ind, 1], 'o')

    temp_coords = np.array(polygon.exterior.coords)
    line_segments = []
    for t0, t1 in zip(temp_coords, temp_coords[1:]):
        line_segments.append([t0, t1])
    ax__.add_collection(LineCollection(line_segments, colors='b', linestyle='solid'))
    line_segments = []
    for simplex in vor_.ridge_vertices:
        simplex = np.asarray(simplex)
        if np.all(simplex >= 0):
            if not all(in_polygon(polygon, vor_.vertices[simplex])):
                continue
            line_segments.append([(x, y) for x, y in vor_.vertices[simplex]])

    ax__.add_collection(LineCollection(line_segments, colors='k', linestyle='solid'))

    line_segments = infinite_segments(vor_)
    from_inside = np.array([x for x in line_segments if polygon.contains(Point(x[0]))])

    line_segments = []

    for f in from_inside:
        for coord0, coord1 in zip(temp_coords, temp_coords[1:]):
            s, t = intersect(f[0], f[1][np.newaxis].T, coord0, coord1)
            if 0 < t < 1 and s > 0:
                line_segments.append([f[0], f[0] + s * f[1]])
                break

    ax__.add_collection(LineCollection(np.array(line_segments), colors='k', linestyle='dashed'))

    line_segments = []

    for v_o_ind in vor_outside_ind:
        for simplex in vor_.ridge_vertices:
            simplex = np.asarray(simplex)
            if np.any(simplex < 0):
                continue
            if np.any(simplex == v_o_ind):
                i = simplex[simplex != v_o_ind][0]
                for coord0, coord1 in zip(temp_coords, temp_coords[1:]):
                    s, t = intersect(
                        vor_.vertices[i],
                        (vor_.vertices[v_o_ind] - vor_.vertices[i])[np.newaxis].T,
                        coord0,
                        coord1
                    )
                    if 0 < t < 1 and 0 < s < 1:
                        line_segments.append([
                            vor_.vertices[i],
                            vor_.vertices[i] + s * (vor_.vertices[v_o_ind] - vor_.vertices[i])
                        ])
                        break

    ax__.add_collection(LineCollection(np.array(line_segments), colors='r', linestyle='dashed'))

    _adjust_bounds(ax__, temp_coords)

    return ax__.figure

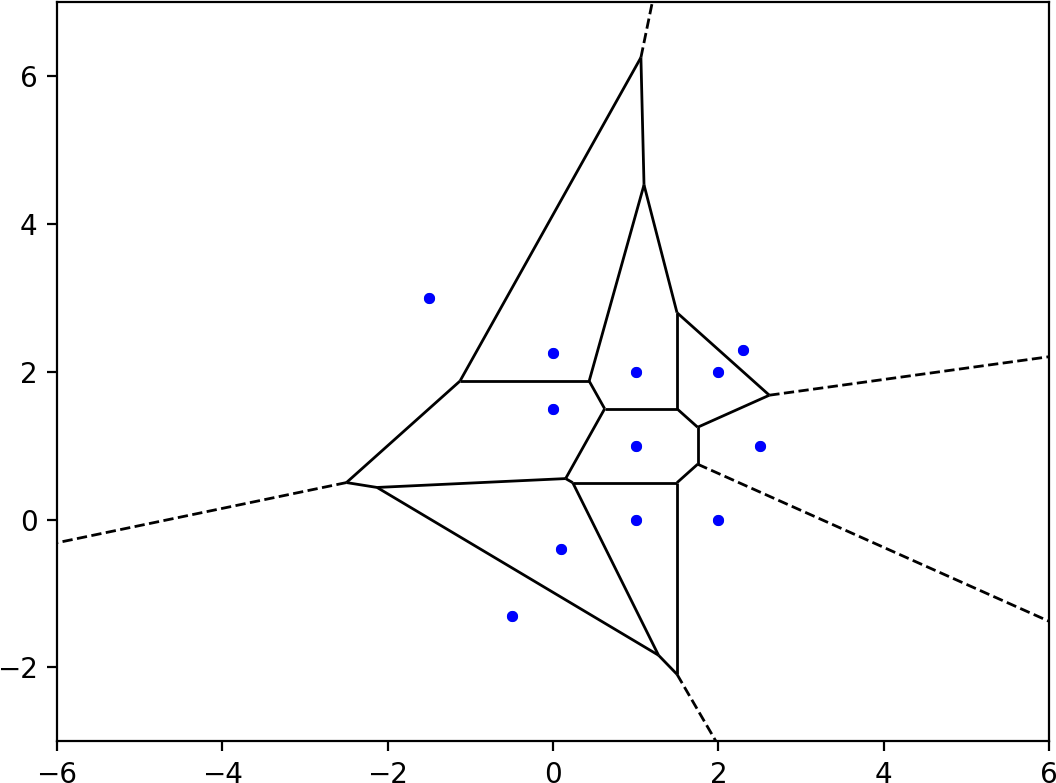
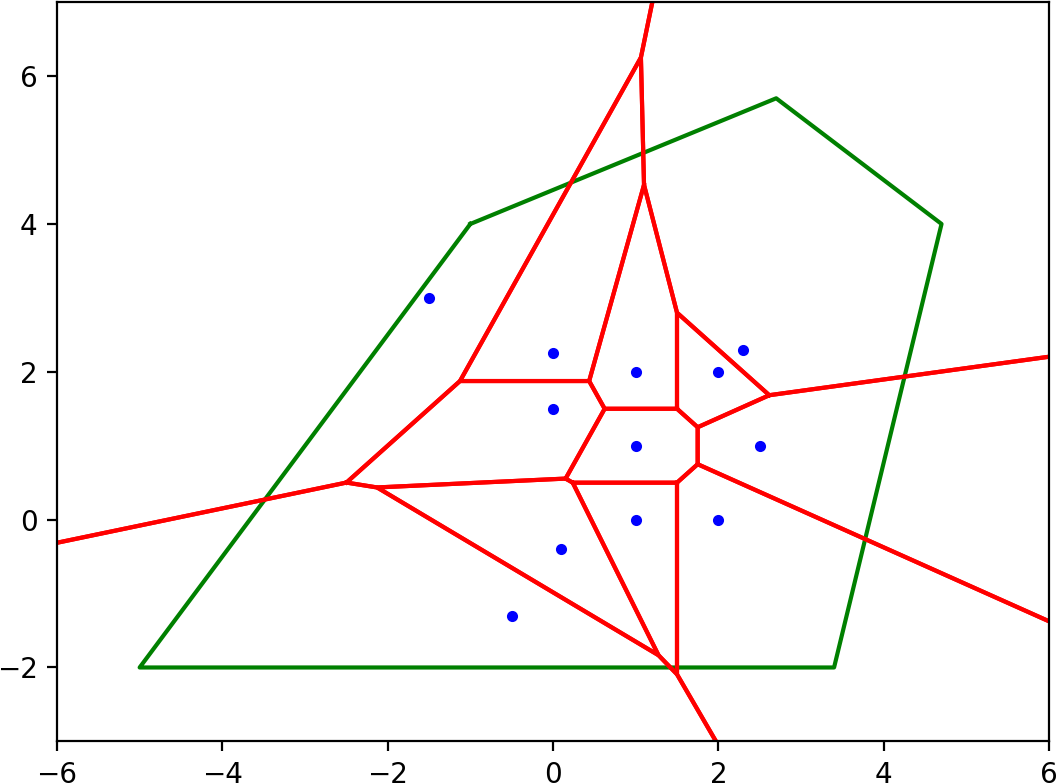
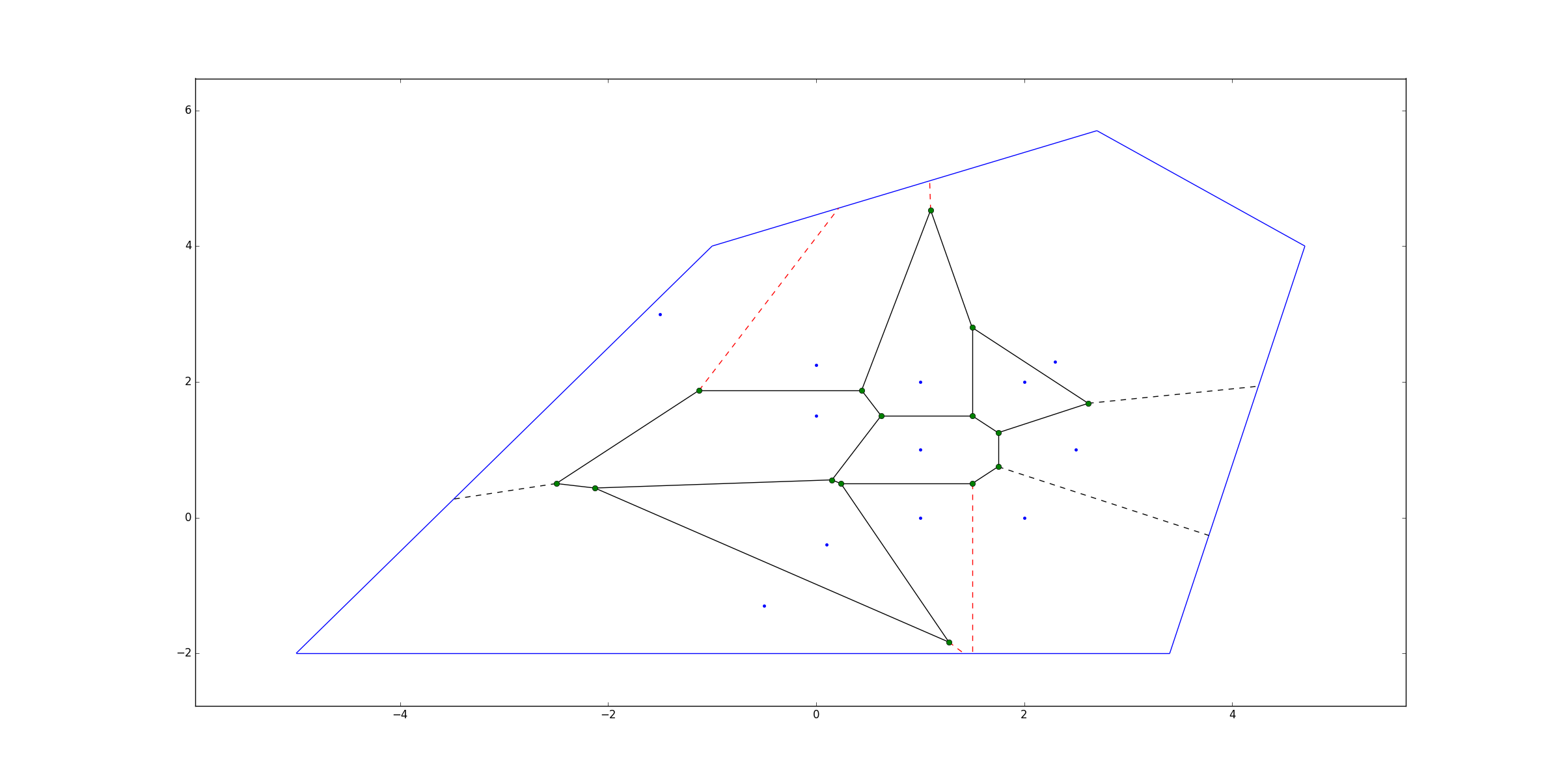
points = np.array([[0.1, -0.4], [0, 1.5], [0, 2.25], [1, 0], [1, 1], [1, 2],
                   [2, 0], [2.5, 1], [2, 2], [2.3, 2.3], [-0.5, -1.3], [-1.5, 3]])

global_boundaries = Polygon([[-5, -2], [3.4, -2], [4.7, 4], [2.7, 5.7], [-1, 4]])
fig = plt.figure()
ax = fig.add_subplot(111)

vor = Voronoi(points)
voronoi_plot_2d_inside_convex_polygon(vor, global_boundaries, ax_=ax)
plt.show()

Note: There are two simple constraints:

1. The polygon must be convex.
2. All the points must be inside the polygon.

colors:

• Original points are in blue.
• Voronoi vertices are in green.
• Finite inner Voronoi ridges are in solid black.
• Finite outer Voronoi ridges are in dashed red.
• Infinite Voronoi ridges are in dashed black.

Cowgill