Multi-threaded algorithm for solving sudoku?

Question

I have a homework assignment to write a multi-threaded sudoku solver, which finds all solutions to a given puzzle. I have previously written a very fast single-threaded backtracking sudoku solver, so I don't need any help with the sudoku solving aspect.

My problem is probably related to not really grokking concurrency, but I don't see how this problem benefits from multi-threading. I don't understand how you can find different solutions to the same problem at the same time without maintaining multiple copies of the puzzle. Given this assumption (please prove it wrong), I don't see how the multi-threaded solution is any more efficient than a single-threaded.

I would appreciate it if anyone could give me some starting suggestions for the algorithm (please, no code...)

---

I forgot to mention, the number of threads to be used is specified as an argument to the program, so as far as I can tell it's not related to the state of the puzzle in any way...

Also, there may not be a unique solution - a valid input may be a totally empty board. I have to report min(1000, number of solutions) and display one of them (if it exists)

Disconnection

It would help if you described your single-threaded algorithm a bit more. – Nickolenicks

actually, it's almost exactly what you've posted :) I find it works quite well & is very easy to code... – Disconnection

Okay, see my additional note below with simple justification for multithreading. – Nickolenicks

Why not just break each row and/or column into it's own thread? – Beaston

@Aaron, it's a lot more than rows and columns, you need to process the 3x3 mini-grids and there's cross-talk between all these elements in a truly efficient solution. – Aeolotropic

Pleased to be of service, glad you like my solution. – Heimer

If your assignment is in C, you should definitely take a look at cilk: cilk.com . It's a C extension (that compiles to ordinary C) that lets you simply 'spawn' function calls, and then collect the results at the end, letting Cilk figure out what to make concurrent. It's very very well suited to this sort of problem. – Engler

Answer 1

Pretty simple really. The basic concept is that in your backtracking solution you would branch when there was a choice. You tried one branch, backtracked and then tried the other choice.

Now, spawn a thread for each choice and try them both simultaneously. Only spawn a new thread if there are < some number of threads already in the system (that would be your input argument), otherwise just use a simple (i.e your existing) single-threaded solution. For added efficiency, get these worker threads from a thread pool.

This is in many ways a divide and conquer technique, you are using the choices as an opportunity to split the search space in half and allocate one half to each thread. Most likely one half is harder than the other meaning thread lifetimes will vary but that is what makes the optimisation interesting.

The easy way to handle the obvious syncronisation issues is to to copy the current board state and pass it into each instance of your function, so it is a function argument. This copying will mean you don't have to worry about any shared concurrency. If your single-threaded solution used a global or member variable to store the board state, you will need a copy of this either on the stack (easy) or per thread (harder). All your function needs to return is a board state and a number of moves taken to reach it.

Each routine that invokes several threads to do work should invoke n-1 threads when there are n pieces of work, do the nth piece of work and then wait with a syncronisation object until all the other threads are finished. You then evaluate their results - you have n board states, return the one with the least number of moves.

Heimer

lots of excellent advice from all, this looks like the best fit for my specific situation. Thanks again all :) – Disconnection

The Java concurrency methods have various executors which allows for a bounded thread pool. Investigate those - it will make your syncronizations much easier. – Solarism

Actually spawning n+1 threads is going to very quickly exhaust all your system resources. You need instead to use a fixed size thread pool - and even that will run into other problems with a big game tree. – Engler

The java Executors will also make it trivial to create a bounded thread pool. – Guillermo

Answer 2

Multi-threading is useful in any situation where a single thread has to wait for a resource and you can run another thread in the meantime. This includes a thread waiting for an I/O request or database access while another thread continues with CPU work.

Multi-threading is also useful if the individual threads can be farmed out to diffent CPUs (or cores) as they then run truly concurrently, although they'll generally have to share data so there'll still be some contention.

I can't see any reason why a multi-threaded Sudoku solver would be more efficient than a single-threaded one, simply because there's no waiting for resources. Everything will be done in memory.

But I remember some of the homework I did at Uni, and it was similarly useless (Fortran code to see how deep a tunnel got when you dug down at 30 degrees for one mile then 15 degrees for another mile - yes, I'm pretty old :-). The point is to show you can do it, not that it's useful.

On to the algorithm.

I wrote a single threaded solver which basically ran a series of rules in each pass to try and populate another square. A sample rule was: if row 1 only has one square free, the number is evident from all the other numbers in row 1.

There were similar rules for all rows, all columns, all 3x3 mini-grids. There were also rules which checked row/column intersects (e.g. if a given square could only contain 3 or 4 due to the row and 4 or 7 due to the column, then it was 4). There were more complex rules I won't detail here but they're basically the same way you solve it manually.

I suspect you have similar rules in your implementation (since other than brute force, I can think of no other way to solve it, and if you've used brute force, there's no hope for you :-).

What I would suggest is to allocate each rule to a thread and have them share the grid. Each thread would do it's own rule and only that rule.

Update:

Jon, based on your edit:

[edit] I forgot to mention, the number of threads to be used is specified as an argument to the program, so as far as I can tell it's not related to the state of the puzzle in any way...

Also, there may not be a unique solution - a valid input may be a totally empty board. I have to report min(1000, number of solutions) and display one of them (if it exists)

It looks like your teacher doesn't want you to split based on the rules but instead on the fork-points (where multiple rules could apply).

By that I mean, at any point in the solution, if there are two or more possible moves forward, you should allocate each possibility to a separate thread (still using your rules for efficiency but concurrently checking each possibility). This would give you better concurrency (assuming threads can be run on separate CPUs/cores) since there will be no contention for the board; each thread will get it's own copy.

In addition, since you're limiting the number of threads, you'll have to work some thread-pool magic to achieve this.

What I would suggest is to have a work queue and N threads. The work queue is initially empty when your main thread starts all the worker threads. Then the main thread puts the beginning puzzle state into the work queue.

The worker threads simply wait for a state to be placed on the work queue and one of them grabs it for processing. The work thread is your single-threaded solver with one small modification: when there are X possibilities to move forward (X > 1), your worker puts X-1 of those back onto the work queue then continues to process the other possibility.

So, lets say there's only one solution (true Sudoku :-). The first worker thread will whittle away at the solution without finding any forks and that will be exactly as in your current situation.

But with two possibilities at move 27 (say, 3 or 4 could go into the top left cell), your thread will create another board with the first possibility (put 3 into that cell) and place that in the work queue. Then it would put 4 in its own copy and continue.

Another thread will pick up the board with 3 in that cell and carry on. That way, you have two threads running concurrently handling the two possibilities.

When any thread decides that its board is insoluble, it throws it away and goes back to the work queue for more work.

When any thread decides that its board is solved, it notifies the main thread which can store it, over-writing any previous solution (first-found is solution) or throw it away if it's already got a solution (last-found is solution) then the worker thread goes back to the work queue for more work. In either case, the main thread should increment a count of solutions found.

When all the threads are idle and the work queue is empty, main either will or won't have a solution. It will also have a count of solutions.

Keep in mind that all communications between workers and main thread will need to be mutexed (I'm assuming you know this based on information in your question).

Aeolotropic

+1 spot on, althought depending on the number of rules or their effectiveness at different stages of the puzzle it might be worth looking at grouping rules rather than having a thread for every rule. – Teredo

If the homework is to make it multi-threaded, you could just divvy up the rules into two sets and give them to two threads. But you may as well go the whole way and allocate one rule per thread. I seem to recall my solution worked with only about 12 rules (I had one rule for all columns, not each column and so on), that should be pretty easy to thread up. – Aeolotropic

Pax - your algorithm that you sketched out will probably only work if there is one unique solution. Once there are two possible choices there are no 'obvious' moves to make. It is as this point that splitting into two threads to try both choices becomes worthwhile. Since all those branches and code loops take time, might as well split them across multiple cores - a great reason to use concurrency. Much more effective than if your program was I/O bound (memory, hdd) – Heimer

Btw, having two threads both evaluate the same board state (i.e splitting rules into two parts) is a total waste of time, you want threads to last MUCH longer than that - multiple states. – Heimer

Tom, it's my contention that Sudoku only has one solution since it's a logic puzzle (others may disagree, but they're wrong :-). – Aeolotropic

There definitely are non-brute force algorithms for solving sudoku puzzles - usually involving backtracking as the original question states – Llamas

Pax, If I give you a blank board, what is the one solution? Note original question. – Heimer

A blank board is not Sudoku. But see my update for handling these abominations :-) – Aeolotropic

@mattb, I know there are non-brute force methods, my answer states I wrote one. I was commenting that the questioner probably had a rule-based solution since the only other choice was brute-force. Brute force would be rubbish for Sudoku unless most of the squares were already populated. – Aeolotropic

Ah - define the problem away, eh Pax? I have only played Suduku a couple of times then just created a simple solver (about 2 years ago) and called it a day. To create the puzzles in the first place you need an algorithm that can create random possible solutions, from which you create the puzzles (remove numbers until a choice appears). Pretend you are trying to create the problems and suddenly the problem gets much more interesting. Especially so if you want to ensure that certain advanced rules are required. Pretend you are the newspaper creating interesting problems. – Heimer

Actually no, @Tom, the creator was not much harder than the solver. The trick bit is getting the numbers in the right place - I did this by doing specific swaps of rows or columns that would not violate the rules of Sudoku and then doing a lot of these random swaps. EG: Can swap column 1 and 2 or 2 and 3 but not 1 and 4. Then to generate the puzzle, remove a random square and make sure the solver can still solve it. Once you've removed all the squares you can, that's your hardest puzzle - putt back 2 for a slightly easier one, 4 for an even easier one and so on. – Aeolotropic

It may just be my engineer's brain but a Sudoku puzzle with mutiple solution is abhorrent to me simply because it comes down to a non-logic decision. Crosswords and Kakuro don't have multiple solutions, why should Soduko? – Aeolotropic

Answer 3

The idea behind multi-threading is taking advantage of having several CPUs, allowing you to make several calculations simultaneously. Of course each thread is going to need its own memory, but that's usually not a problem.

Mostly, what you want to do is divide the possible solution state into several sub-spaces which are as independent as possible (to avoid having to waste too many resources on thread creation overhead), and yet "fit" your algorithm (to actually benefit from having multiple threads).

Inocenciainoculable

Answer 4

Here is a greedy brute-force single-threaded solver:

1. Select next empty cell. If no more empty cells, victory!
2. Possible cell value = 1
3. Check for invalid partial solution (duplicates in row, column or 3x3 block).
4. If partial solution is invalid, increment cell value and return to step 3. Otherwise, go to step 1.

If you look at the above outline, the combination of steps 2 and 3 are obvious candidates for multithreading. More ambitious solutions involve creating a recursive exploration that spawns tasks that are submitted to a thread pool.

EDIT to respond to this point: "I don't understand how you can find different solutions to the same problem at the same time without maintaining multiple copies of the puzzle."

You can't. That's the whole point. However, a concrete 9-thread example might make the benefits more clear:

1. Start with an example problem.
2. Find the first empty cell.
3. Create 9 threads, where each thread has its own copy of the problem with its own index as a candidate value in the empty cell.
4. Within each thread, run your original single-threaded algorithm on this thread-local modified copy of the problem.
5. If one of the threads finds an answer, stop all the other threads.

As you can imagine, each thread is now running a slightly smaller problem space and each thread has the potential to run on its own CPU core. With a single-threaded algorithm alone, you can't reap the benefits of a multi-core machine.

Nickolenicks

If your 9 worker threads can't spawn new threads of their own, there is a good chance that most of them will immediately run out of work to do leaving you with only 1 or 2 threads. You need to repeat the branching at multiple levels to get a solution that will scale to many processors. – Heimer

Actually, for really pathological cases, you won't necessarily find the dead-ends that quickly. That said, it's true that a sophisticated multithreaded solver would need to keep the thread pool well-stocked with partial solutions to work on. However, this isn't MY homework.... ;-) – Nickolenicks

For example, see Gordon Royle's site where he is generating minimal problems: people.csse.uwa.edu.au/gordon/sudokumin.php Very nasty even with multithreading. – Nickolenicks

Answer 5

TL;DR

Yes, a backtracking-based Sudoku solver can, depending on the puzzle, benefit considerably from parallelization! A puzzle's search space can be modeled as a tree data structure, and backtracking performs a depth-first search (DFS) of this tree, which is inherently not parallelizable. However, by combining DFS with its opposite form of tree traversal, breadth-first search (BFS), parallelism can be unlocked. This is because BFS allows multiple independent sub-trees to be discovered simultaneously, which can then be searched in parallel.

Because BFS unlocks parallelism, employing it warrants the use of a global thread-safe queue, onto/from which the discovered sub-trees can be pushed/popped by all threads, and this entails significant performance overhead compared to DFS. Hence parallelizing such a solver requires fine-tuning the amount of BFS carried out such that just enough is performed to ensure the traversal of the tree is sufficiently parallelized but not too much such that the overhead of thread communication (pushing/popping sub-trees of the queue) outweighs the speedup parallelization provides.

I parallelized a backtracking-based Sudoku solver a while back, and implemented 4 different parallel solver variants along with a sequential (single-threaded) solver. The parallel variants all combined DFS and BFS in different ways and to varying extents, and the fastest variant was on average over three times as fast as the single-threaded solver (see the graph at the bottom).

Also, to answer your question, in my implementation each thread receives a copy of the initial puzzle (once when the thread is spawned) so the required memory is slightly higher than the sequential solver - which is not uncommon when parallelizing something. But that's the only "inefficiency" as you put it: As mentioned above, if the amount of BFS is appropriately fine-tuned, the attainable speedup via parallelization greatly outweighs the parallel overhead from thread communication as well as the higher memory footprint. Also, while my solvers assumed unique solutions, extending them to handle non-proper puzzles and find all their solutions would be simple and wouldn't significantly, if at all, reduce the speedup, due to the nature of the solver's design. See the full answer below for more details.

---

FULL ANSWER

Whether a Sudoku solver benefits from multithreading strongly depends on its underlying algorithm. Common approaches such as constraint propagation (i.e. a rule-based method) where the puzzle is modeled as a constraint satisfaction problem, or stochastic search, don't really benefit since single-threaded solvers using these approaches are already exceptionally fast. Backtracking however, can benefit considerably most of the time (depending on the puzzle).

As you probably already know, a Sudoku's search space can be modeled as a tree data structure: The first level of the three represents the first empty cell, the second level the second empty cell, and so on. At each level, the nodes represent the potential values of that cell given the values of their ancestor nodes. Thus searching this space can be parallelized by searching independent sub-trees at the same time. A single-threaded backtracking solver must traverse the whole tree by itself, one sub-tree after another, but a parallel solver can have each thread search a separate sub-tree in parallel.

There are multiple ways to realize this, but they're all based on the principle of combining depth-first search (DFS) with breadth-first search (BFS), which are two (opposite) forms of tree traversal. A single-threaded backtracking solver only carries out DFS the entire search, which is inherently non-parallelizable. By adding BFS into the mix however, parallelism can be unlocked. This is because BFS traverses the tree level-by-level (as opposed to branch-by-branch with DFS) and thereby finds all possible nodes on a given level before moving to the next lower level, whereas DFS takes the first possible node and completely searches its sub-tree before moving to the next possible node. As a result, BFS enables multiple independent sub-trees to be discovered right away that can then be searched by separate threads; DFS doesn't know anything about additional independent sub-trees right from the get go, because it's busy searching the first one it finds in a depth-first manner.

As is usually the case with multi-threading, parallelizing your code is tricky and initial attempts often decrease performance if you don't know exactly what you're doing. In this case, it's important to realize that BFS is much slower than DFS, so the chief concern is tweaking the amount of DFS and BFS you carry out such that just enough BFS is executed in order to unlock the ability to discover multiple sub-trees simultaneously, but also minimizing it so its slowness doesn't end up outweighing that ability. Note that BFS isn't inherently slower than DFS, it's just that the threads need access to the discovered sub-trees so they can search them. Thus BFS requires a global thread-safe data structure (e.g. a queue) onto/from which the sub-trees can be pushed/popped by separate threads, and this entails significant overhead compared to DFS which doesn't require any communication between threads. Hence parallelizing such a solver is a fine-tuning process and one wants to conduct enough BFS to provide all threads with enough sub-trees to search (i.e. achieve a good load balancing among all threads) while minimizing the communication between threads (the pushing/popping of sub-trees onto/off the queue).

I parallelized a backtracking-based Sudoku solver a while back, and implemented 4 different parallel solver variants and benchmarked them against a sequential (single-threaded) solver which I also implemented. They were all implemented in C++. The best (fastest) parallel variant's algorithm was as follows:

• Start with a DFS of the puzzle's tree, but only do it down to a certain level, or search-depth
• At the search-depth, conduct a BFS and push all the sub-trees discovered at that level onto the global queue
• The threads then pop these sub-trees off the queue and perform a DFS on them, all the way down to the last level (the last empty cell).

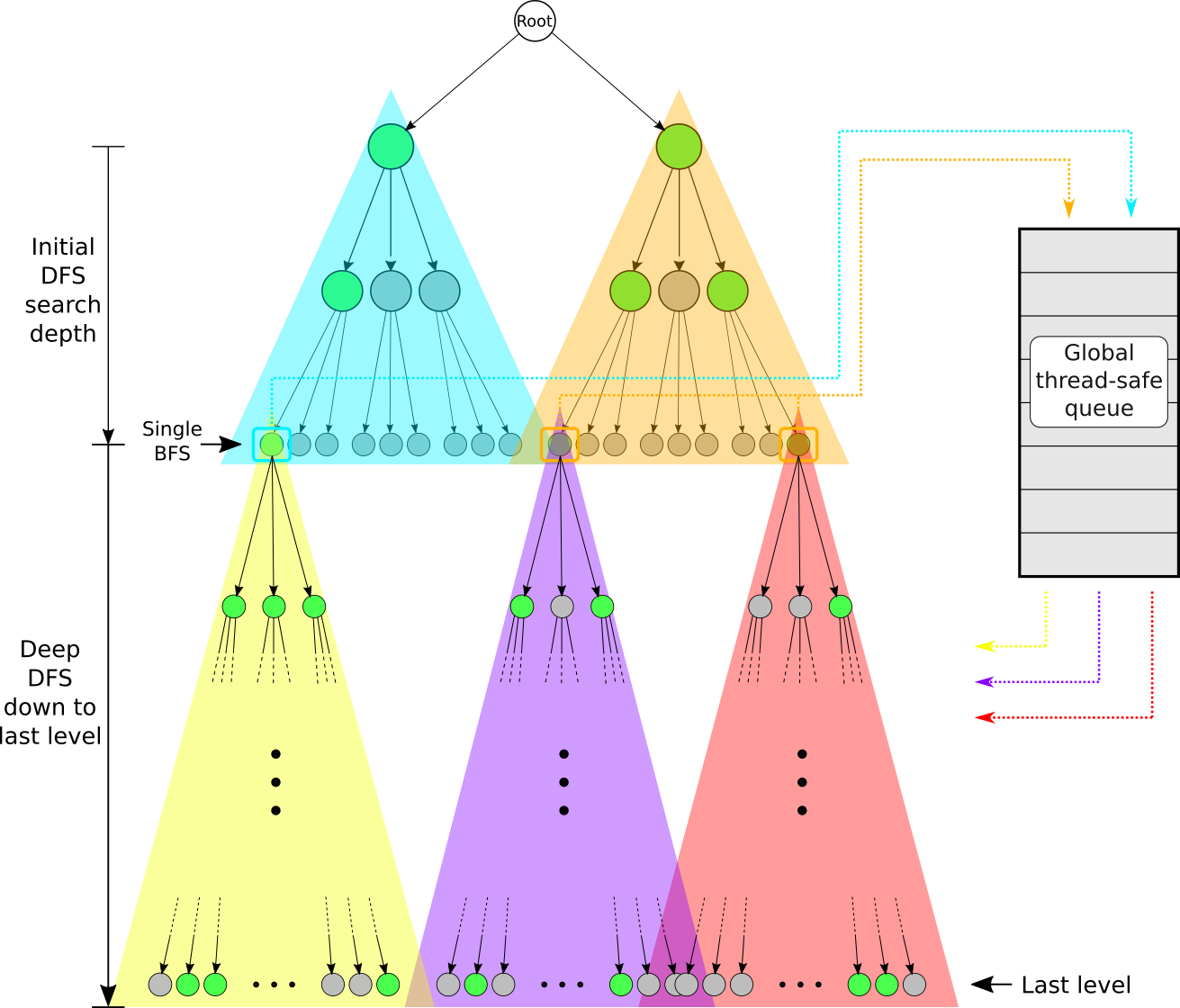
The following figure (taken from my report from back then) illustrates these steps: The different color triangles represent different threads and the sub-trees they traverse. The green nodes represent allowed cell values on that level. Note the single BFS carried out at the search-depth; The sub-trees discovered at this level (yellow, purple, and red) are pushed onto the global queue, which are then traversed independently in parallel all the way down to the last level (last empty cell) of the tree.

As you can see, this implementation performs a BFS of only one level (at the search-depth). This search-depth is adjustable, and optimizing it represents the aforementioned fine-tuning process. The deeper the search-depth, the more BFS is carried out since a tree's width (# nodes on a given level) naturally increases the further down you go. Interestingly, the optimal search depth is typically at a quite shallow level (i.e. a not very deep level in the tree); This reveals that conducting even a small amount of BFS is already enough to generate ample sub-trees and provide a good load balance among all threads.

Also, thanks to the global queue, an arbitrary number of threads can be chosen. It's generally a good idea though to set the number of threads equal to the number of hardware threads (i.e. # logical cores); Choosing more typically won't further increase performance. Furthermore, it's also possible to parallelize the initial DFS performed at the start by performing a BFS of the first level of the tree (first empty cell): the sub-trees discovered at level 1 are then traversed in parallel, each thread stopping at the given search-depth. This is what's done in the figure above. This isn't strictly necessary though as the optimal search depth is typically quite shallow as mentioned above, hence a DFS down to the search-depth is still very quick even if it's single-threaded.

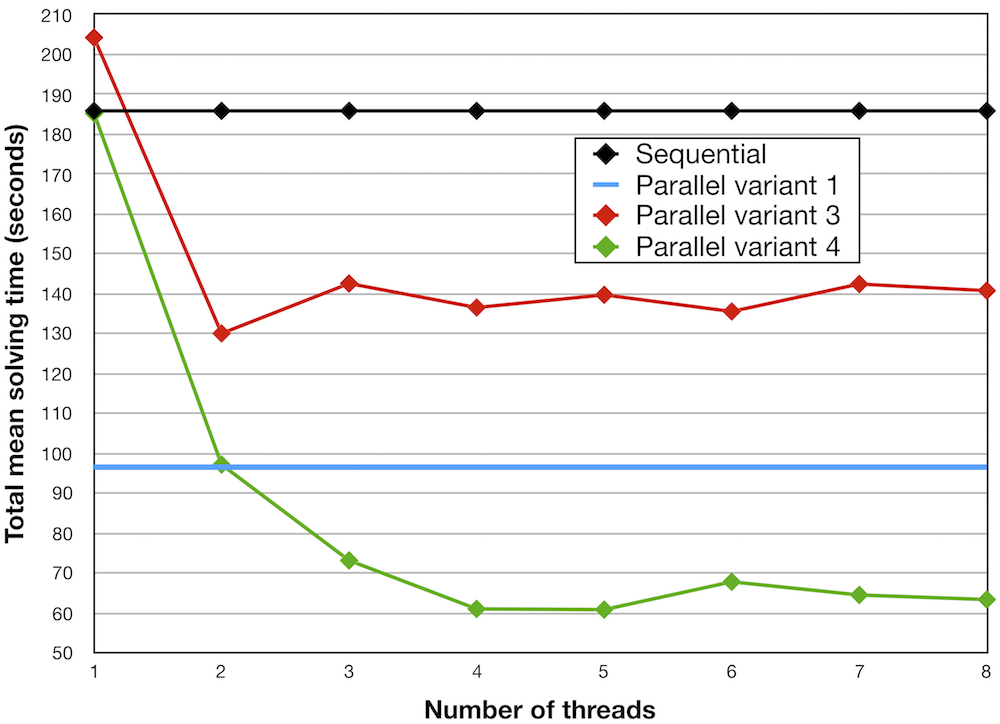
I thoroughly tested all solvers on 14 different Sudoku puzzles (specifically, a select set of puzzles specially designed to be difficult for a backtracking solver), and the figure below shows each solver's average time taken to solve all puzzles, for various thread counts (my laptop has four hardware threads). Parallel variant 2 isn't shown because it actually achieved significantly worse performance than the sequential solver. With parallel variant 1, the # threads was automatically determined during run-time, and depended on the puzzle (specifically, the branching factor of the first level); Hence the blue line represents its average total solving time regardless of the thread count.

All parallel solver variants combine DFS and BFS in different ways and to varying extents. When utilizing 4 threads, the fastest parallel solver (variant 4) was on average over three times as fast as the single-threaded solver!

Chrisoula

Answer 6

When you say all solutions to a given puzzle, do you mean the final one and only solution to the puzzle? Or the different ways of arriving at the one solution? I was of the understanding that by definition, a sudoku puzzle could have only one solution...

For the former, either Pax's rule based approach or Tom Leys' take on multi-threading your existing backtracking algorithm might be the way to go.

If the latter, you could implement some kind of branching algorithm which launches a new thread (with it's own copy of the puzzle) for each possible move at each stage of the puzzle.

Teredo

I think a Sudoku puzzle can have multiple solutions. You can get to a point where you have 4 cells that can have 1 of 2 numbers, either number will work as long as the other cells are consistent. I found this while writing an Excel solver/hinter. – Grandioso

if that is the case then it is not a true sudoku, otherwise a lot of the advanced techniques which rely on this principle are worthless – Teredo

Sudoku should only have one solution. That's a given. – Aeolotropic

If a client gives you multi-solution sudoku puzzles you can either get insist they are not proper sudoku problems and ask that the data being given to your application is changed, or you can write an application that solves these "improper" sudoku puzzles the way the client wants. Guess which approach is more likely to help you in the real world? :-) – Osteoblast

that's the whole point, if the client gives you a multi-solution puzzle it's not a sudoku. There's probably another name for a broken one. – Teredo

Either way, your program shouldn't hang, it might however flag that the input is invalid as it hands out one of many possible results. – Heimer

Answer 7

Does it need to benefit from multithreading, or just make use of multthreading so you can learn for the assignment?

If you use a brute force algoritm it is rather easy to split into multiple threads, and if the assignment is focused on coding threads that may be an acceptable solution.

Osteoblast

Answer 8

Depending on how you coded your single threaded solver, you might be able to re-use the logic. You can code a multi-threaded solver to start each thread using a different set of strategies to solve the puzzle.

Using those different strategies, your multi-threaded solver may find the total set of solutions in less time than your single threaded solver (keep in mind though that a true Sudoku puzzle only has one solution...you're not the only one who had to deal with that god awful game in class)

Dioxide

Answer 9

Some general points: I don't run processes in parallel unless 1) it is easy to divide the problem 2) I know I'll get a benefit to doing so - e.g. I won't hit another bottleneck. I entirely avoid sharing mutable values between threads - or minimize it. Some people are smart enough to work safely with mutexes. I'm not.

You need to find points in your algorithm that create natural branches or large units of work. Once you've identified a unit to work, you drop it in a queue for a thread to pick up. As a trivial example. 10 databases to upgrade. Start upgrade async on all 10 servers. Wait for all to complete. I can easily avoid sharing state between threads / processes, and can easily aggregate the results.

What comes to mind for sudoku is that an efficient suduko solution should combining 2-3 (or more) strategies that never run past a certain depth. When I do Sudoku, it's apparent that, at any given moment, different algorithms provide the solution with the least work. You could simply fire off a handful of strategies, let them investigate to a limited depth, wait for report. Rinse, repeat. This avoids "brute-forcing" the solution. Each algorithm has it's own data space, but you combine the answers.

Sciam.com had article on this a year or two back - looks like it isn't public, though.

Salangia

Suduku has a very small search space, leaving little benefit from the iterative deepening that you describe. Perhaps on a 15*15 or 25*25 imaginary board. – Heimer

Answer 10

You said you used back tracking to solve the problem. What you can do is to split the search space into two and handle each space to a thread, then each thread would do the same till you reach the last node. I did a solution to this which can be found www2.cs.uregina.ca/~hmer200a but using single thread but the mechanism of splitting the search space is there using branch and bound.

Shakespeare

Answer 11

A few years ago when I looked at solving sudoku, it seemed like the optimal solution used a combination of logical analysis algorithms and only fell back on brute force when necessary. This allowed the solver to find the solution very quickly, and also rank the board by difficulty if you wanted to use it to generate a new puzzle. If you took this approach you could certainly introduce some concurrency, although having the threads actually work together might be tricky.

Syncretism

Answer 12

I have an idea that's pretty fun here.. do it with the Actor Model! I'd say using erlang.. How? You start with the original board, and..

• 1) at first empty cell create 9 children with different number, then commit suicide
• 2) each child check if it's invalid, if so it commits suicide, else
  • if there is an empty cell, go to 1)
  • if complete, this actor is a solution

Clearly every surviving actor is a solution to the problem =)

Duval

Answer 13

Just a side note. I actually implemented an optimized sudoku solver and looked into multithreading, but two things stopped me.

First, the simple overhead of starting a thread took 0.5 milliseconds, while the whole resolution took between 1 to 3 milliseconds (I used Java, other languages or environments may give different results).

Second, most problems don't require any backtracking. And those that do, only need it late in the resolution of the problem, once all game rules have been exhausted and we need to make an hypothesis.

Drud

Answer 14

Here's my own penny. Hope it helps.

Remember that inter-processor/inter-thread communications are expensive. Don't multi-thread unless you have to. If there isn't much work/computation to be done in other threads, you might as well just go on with a single-thread.

Try as much as possible to avoid sharing data between threads. Use them only when necessary

Take advantage of SIMD extensions wherever possible. With the Vector Extensions you can perform calculations on multiple data in a single swoop. It can help you aplenty.

Nuke