Finding all the combinations of free polyominoes within a specific area with a SAT-solver (Python)

Question

I am new to the world of SAT solvers and would need some guidance regarding the following problem.

Considering that:

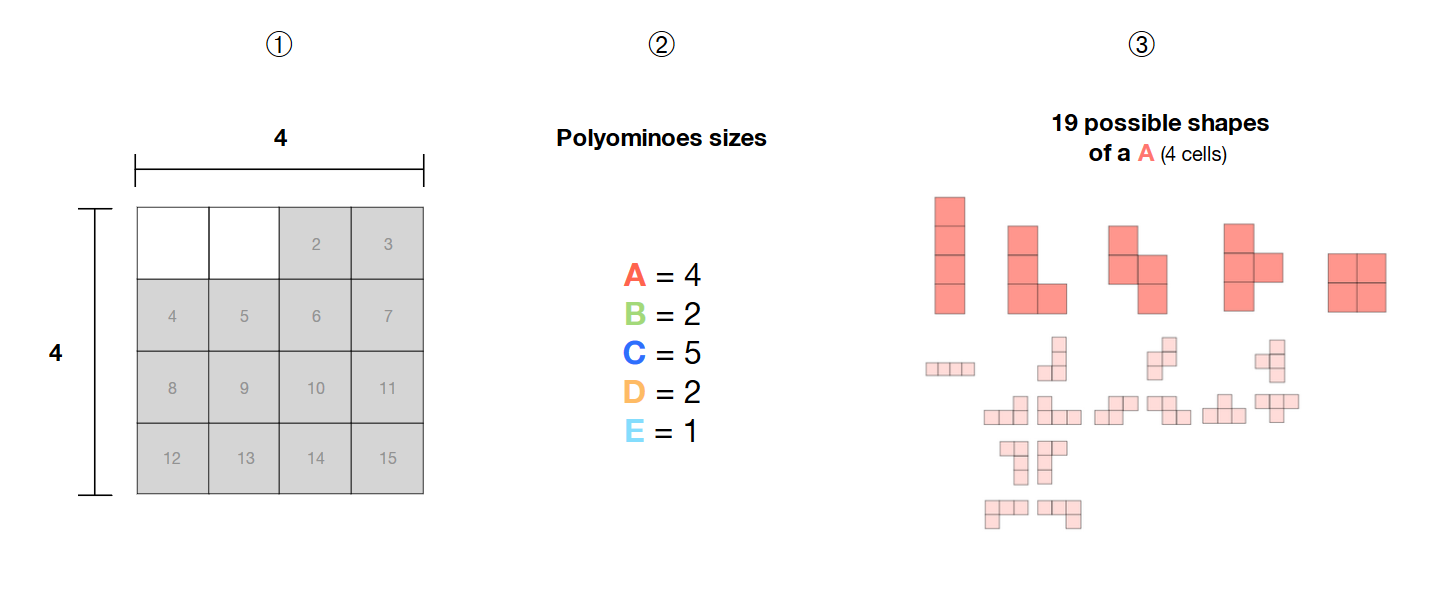
❶ I have a selection of 14 adjacent cells in a 4*4 grid

❷ I have 5 polyominoes (A, B, C, D, E) of sizes 4, 2, 5, 2 and 1

❸ these polyominoes are free, i.e. their shape is not fixed and can form different patterns

How can I compute all the possible combinations of these 5 free polyominoes inside the selected area (cells in grey) with a SAT-solver ?

Borrowing both from @spinkus's insightful answer and the OR-tools documentation I could make the following example code (runs in a Jupyter Notebook):

from ortools.sat.python import cp_model

import numpy as np
import more_itertools as mit
import matplotlib.pyplot as plt
%matplotlib inline


W, H = 4, 4 #Dimensions of grid
sizes = (4, 2, 5, 2, 1) #Size of each polyomino
labels = np.arange(len(sizes))  #Label of each polyomino

colors = ('#FA5454', '#21D3B6', '#3384FA', '#FFD256', '#62ECFA')
cdict = dict(zip(labels, colors)) #Color dictionary for plotting

inactiveCells = (0, 1) #Indices of disabled cells (in 1D)
activeCells = set(np.arange(W*H)).difference(inactiveCells) #Cells where polyominoes can be fitted
ranges = [(next(g), list(g)[-1]) for g in mit.consecutive_groups(activeCells)] #All intervals in the stack of active cells



def main():
    model = cp_model.CpModel()


    #Create an Int var for each cell of each polyomino constrained to be within Width and Height of grid.
    pminos = [[] for s in sizes]
    for idx, s in enumerate(sizes):
        for i in range(s):
            pminos[idx].append([model.NewIntVar(0, W-1, 'p%i'%idx + 'c%i'%i + 'x'), model.NewIntVar(0, H-1, 'p%i'%idx + 'c%i'%i + 'y')])



    #Define the shapes by constraining the cells relative to each other

    ## 1st polyomino -> tetromino ##
    #                              #      
    #                              # 
    #            #                 # 
    #           ###                # 
    #                              # 
    ################################

    p0 = pminos[0]
    model.Add(p0[1][0] == p0[0][0] + 1) #'x' of 2nd cell == 'x' of 1st cell + 1
    model.Add(p0[2][0] == p0[1][0] + 1) #'x' of 3rd cell == 'x' of 2nd cell + 1
    model.Add(p0[3][0] == p0[0][0] + 1) #'x' of 4th cell == 'x' of 1st cell + 1

    model.Add(p0[1][1] == p0[0][1]) #'y' of 2nd cell = 'y' of 1st cell
    model.Add(p0[2][1] == p0[1][1]) #'y' of 3rd cell = 'y' of 2nd cell
    model.Add(p0[3][1] == p0[1][1] - 1) #'y' of 3rd cell = 'y' of 2nd cell - 1



    ## 2nd polyomino -> domino ##
    #                           #      
    #                           # 
    #           #               # 
    #           #               # 
    #                           # 
    #############################

    p1 = pminos[1]
    model.Add(p1[1][0] == p1[0][0])
    model.Add(p1[1][1] == p1[0][1] + 1)



    ## 3rd polyomino -> pentomino ##
    #                              #      
    #            ##                # 
    #            ##                # 
    #            #                 # 
    #                              #
    ################################

    p2 = pminos[2]
    model.Add(p2[1][0] == p2[0][0] + 1)
    model.Add(p2[2][0] == p2[0][0])
    model.Add(p2[3][0] == p2[0][0] + 1)
    model.Add(p2[4][0] == p2[0][0])

    model.Add(p2[1][1] == p2[0][1])
    model.Add(p2[2][1] == p2[0][1] + 1)
    model.Add(p2[3][1] == p2[0][1] + 1)
    model.Add(p2[4][1] == p2[0][1] + 2)



    ## 4th polyomino -> domino ##
    #                           #      
    #                           # 
    #           #               #   
    #           #               # 
    #                           # 
    #############################

    p3 = pminos[3]
    model.Add(p3[1][0] == p3[0][0])
    model.Add(p3[1][1] == p3[0][1] + 1)



    ## 5th polyomino -> monomino ##
    #                             #      
    #                             # 
    #           #                 # 
    #                             # 
    #                             # 
    ###############################
    #No constraints because 1 cell only



    #No blocks can overlap:
    block_addresses = []
    n = 0
    for p in pminos:
        for c in p:
            n += 1
            block_address = model.NewIntVarFromDomain(cp_model.Domain.FromIntervals(ranges),'%i' % n)
                model.Add(c[0] + c[1] * W == block_address)
                block_addresses.append(block_address)

    model.AddAllDifferent(block_addresses)



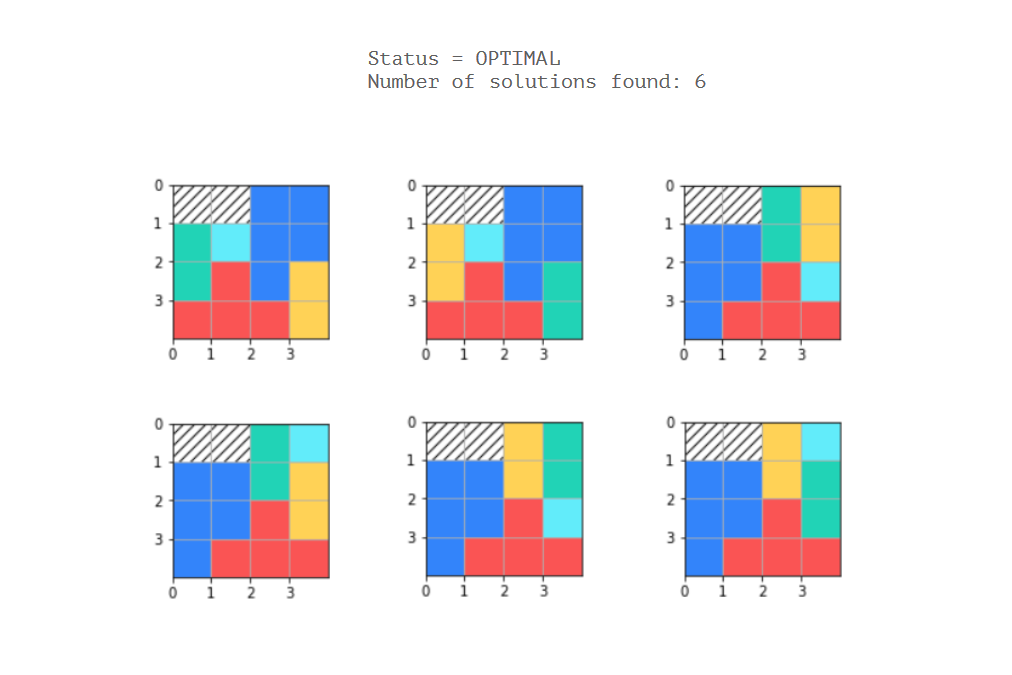
    #Solve and print solutions as we find them
    solver = cp_model.CpSolver()

    solution_printer = SolutionPrinter(pminos)
    status = solver.SearchForAllSolutions(model, solution_printer)

    print('Status = %s' % solver.StatusName(status))
    print('Number of solutions found: %i' % solution_printer.count)




class SolutionPrinter(cp_model.CpSolverSolutionCallback):
    ''' Print a solution. '''

    def __init__(self, variables):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.variables = variables
        self.count = 0

    def on_solution_callback(self):
        self.count += 1


        plt.figure(figsize = (2, 2))
        plt.grid(True)
        plt.axis([0,W,H,0])
        plt.yticks(np.arange(0, H, 1.0))
        plt.xticks(np.arange(0, W, 1.0))


        for i, p in enumerate(self.variables):
            for c in p:
                x = self.Value(c[0])
                y = self.Value(c[1])
                rect = plt.Rectangle((x, y), 1, 1, fc = cdict[i])
                plt.gca().add_patch(rect)

        for i in inactiveCells:
            x = i%W
            y = i//W
            rect = plt.Rectangle((x, y), 1, 1, fc = 'None', hatch = '///')
            plt.gca().add_patch(rect)

The problem is that I have hard-coded 5 unique/fixed polyominoes and I don't know to how define the constraints so as each possible pattern for each polyomino is taken into account (provided it is possible).

Arabele

I hear about Google OR-tools first time. Is it possible to use standard Python libraries such as itertools, numpy, networkx? – Drunkard

I would prefer to use a sat-solver, or-tools preferably. – Arabele

@Arabele it is pretty easy to model/solve this kind of problem using the MiniZinc language, since there are high-level constraints for placing irregular objects on a surface. If you walk through the free course "Advanced Modeling for Discrete Optimization" on Coursera, you are actually going to be taught how to do it and given some practical (and more complex) examples. Or-Tools has an interface for the MiniZinc language, so you can still harness its power to find a quick solution. – Aurum

Seems interesting, thanks for the pointer. Not sure it will answer the specific problem that I have (defining constraints involving free polyominoes, not static) but I'll definitely have a look at it. – Arabele

@Arabele One can provide as many alternative shapes of A in MiniZinc, it is actually pretty easy to do that. These shapes need to be precomputed (rotations included). Anyway, if any shape is allowed --as long as it is connected-- then is probably much easier to encode the problem with a bunch of linear constraints on the x,y coordinates and forget about shapes entirely. – Aurum

@PatrickTrentin Thank you for the hints. If I open the question to other languages than Python, would you like to provide an answer ? – Arabele

@Arabele it might take some time right now, how urgent is this for you? – Aurum

I'd say a couple of weeks, but the bounty will be over by then. It would make more sense if it is awarded to the person that truly provides a solution. – Arabele

@Arabele thanks for your concern about the bounty, but it's not truly important here. What's important is that you get a useful answer. I may be able to write down something in this amount of time. Please poke me back if I forget to write something before the end of this week – Aurum

I must apologize, I had completely forgotten about this question. There has been a related question in the minizinc tag with a detailed answer that covers my previous suggestion about using minizinc. – Aurum

Thank you Patrick ! – Arabele

Answer 1

One relatively straightforward way to constrain a simply connected region in OR-Tools is to constrain its border to be a circuit. If all your polyominos are to have size less than 8, we don’t need to worry about non-simply connected ones.

This code finds all 3884 solutions:

from ortools.sat.python import cp_model

cells = {(x, y) for x in range(4) for y in range(4) if x > 1 or y > 0}
sizes = [4, 2, 5, 2, 1]
num_polyominos = len(sizes)
model = cp_model.CpModel()

# Each cell is a member of one polyomino
member = {
    (cell, p): model.NewBoolVar(f"member{cell, p}")
    for cell in cells
    for p in range(num_polyominos)
}
for cell in cells:
    model.Add(sum(member[cell, p] for p in range(num_polyominos)) == 1)

# Each polyomino contains the given number of cells
for p, size in enumerate(sizes):
    model.Add(sum(member[cell, p] for cell in cells) == size)

# Find the border of each polyomino
vertices = {
    v: i
    for i, v in enumerate(
        {(x + i, y + j) for x, y in cells for i in [0, 1] for j in [0, 1]}
    )
}
edges = [
    edge
    for x, y in cells
    for edge in [
        ((x, y), (x + 1, y)),
        ((x + 1, y), (x + 1, y + 1)),
        ((x + 1, y + 1), (x, y + 1)),
        ((x, y + 1), (x, y)),
    ]
]
border = {
    (edge, p): model.NewBoolVar(f"border{edge, p}")
    for edge in edges
    for p in range(num_polyominos)
}
for (((x0, y0), (x1, y1)), p), border_var in border.items():
    left_cell = ((x0 + x1 + y0 - y1) // 2, (y0 + y1 - x0 + x1) // 2)
    right_cell = ((x0 + x1 - y0 + y1) // 2, (y0 + y1 + x0 - x1) // 2)
    left_var = member[left_cell, p]
    model.AddBoolOr([border_var.Not(), left_var])
    if (right_cell, p) in member:
        right_var = member[right_cell, p]
        model.AddBoolOr([border_var.Not(), right_var.Not()])
        model.AddBoolOr([border_var, left_var.Not(), right_var])
    else:
        model.AddBoolOr([border_var, left_var.Not()])

# Each border is a circuit
for p in range(num_polyominos):
    model.AddCircuit(
        [(vertices[v0], vertices[v1], border[(v0, v1), p]) for v0, v1 in edges]
        + [(i, i, model.NewBoolVar(f"vertex_loop{v, p}")) for v, i in vertices.items()]
    )

# Print all solutions
x_range = range(min(x for x, y in cells), max(x for x, y in cells) + 1)
y_range = range(min(y for x, y in cells), max(y for x, y in cells) + 1)
solutions = 0


class SolutionPrinter(cp_model.CpSolverSolutionCallback):
    def OnSolutionCallback(self):
        global solutions
        solutions += 1
        for y in y_range:
            print(
                *(
                    next(
                        p
                        for p in range(num_polyominos)
                        if self.Value(member[(x, y), p])
                    )
                    if (x, y) in cells
                    else "-"
                    for x in x_range
                )
            )
        print()


solver = cp_model.CpSolver()
solver.SearchForAllSolutions(model, SolutionPrinter())
print("Number of solutions found:", solutions)

Accomplished

My apologies for the late reply, I got carried away by another project of mine and forgot about this topic. Thank you for providing a working example with OR-Tools. – Arabele

Answer 2

EDIT: I missed the word "free" in original answer and gave answer using OR-Tools for fixed polyominoes. Added a section to answer to include a solution for free polyominoes - which AFAICT turns out to be quite difficult to express precisely in constraint programming with OR-Tools.

FIXED POLYOMINOES WITH OR-TOOLS:

Yeah you can do it with constraint programming in OR-Tools. OR-Tools knows nothing about 2D grid geometry so you have to encode the geometry of each shape you have in terms of positional constraints. I.e. a shape is a collection of blocks / cells that must have a certain relationship to each other, must be within the bounds of the grid and must not overlap. Once you have your constraint model you just ask the CP-SAT Solver to solve it, in your case, for all possible solutions.

Here is a really simple proof of concept with two rectangle shapes on a 4x4 grid (you'd also probably want to add some kind of interpreter code to go from shape descriptions to a set of OR-Tools variables and constraints in a larger scale problem since inputting the constraints by hand is a bit tedious).

from ortools.sat.python import cp_model

(W, H) = (3, 3) # Width and height of our grid.
(X, Y) = (0, 1) # Convenience constants.


def main():
  model = cp_model.CpModel()
  # Create an Int var for each block of each shape constrained to be within width and height of grid.
  shapes = [
    [
      [ model.NewIntVar(0, W, 's1b1_x'), model.NewIntVar(0, H, 's1b1_y') ],
      [ model.NewIntVar(0, W, 's1b2_x'), model.NewIntVar(0, H, 's1b2_y') ],
      [ model.NewIntVar(0, W, 's1b3_x'), model.NewIntVar(0, H, 's1b3_y') ],
    ],
    [
      [ model.NewIntVar(0, W, 's2b1_x'), model.NewIntVar(0, H, 's2b1_y') ],
      [ model.NewIntVar(0, W, 's2b2_x'), model.NewIntVar(0, H, 's2b2_y') ],
    ]
  ]

  # Define the shapes by constraining the blocks relative to each other.
  # 3x1 rectangle:
  s0 = shapes[0]
  model.Add(s0[0][Y] == s0[1][Y])
  model.Add(s0[0][Y] == s0[2][Y])
  model.Add(s0[0][X] == s0[1][X] - 1)
  model.Add(s0[0][X] == s0[2][X] - 2)
  # 1x2 rectangle:
  s1 = shapes[1]
  model.Add(s1[0][X] == s1[1][X])
  model.Add(s1[0][Y] == s1[1][Y] - 1)

  # No blocks can overlap:
  block_addresses = []
  for i, block in enumerate(blocks(shapes)):
    block_address = model.NewIntVar(0, (W+1)*(H+1), 'b%d' % (i,))
    model.Add(block[X] + (H+1)*block[Y] == block_address)
    block_addresses.append(block_address)
  model.AddAllDifferent(block_addresses)

  # Solve and print solutions as we find them
  solver = cp_model.CpSolver()
  solution_printer = SolutionPrinter(shapes)
  status = solver.SearchForAllSolutions(model, solution_printer)
  print('Status = %s' % solver.StatusName(status))
  print('Number of solutions found: %i' % solution_printer.count)


def blocks(shapes):
  ''' Helper to enumerate all blocks. '''
  for shape in shapes:
    for block in shape:
      yield block


class SolutionPrinter(cp_model.CpSolverSolutionCallback):
    ''' Print a solution. '''

    def __init__(self, variables):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.variables = variables
        self.count = 0

    def on_solution_callback(self):
      self.count += 1
      solution = [(self.Value(block[X]), self.Value(block[Y])) for shape in self.variables for block in shape]
      print((W+3)*'-')
      for y in range(0, H+1):
        print('|' + ''.join(['#' if (x,y) in solution else ' ' for x in range(0, W+1)]) + '|')
      print((W+3)*'-')


if __name__ == '__main__':
  main()

Gives:

...
------
|    |
| ###|
|  # |
|  # |
------
------
|    |
| ###|
|   #|
|   #|
------
Status = OPTIMAL
Number of solutions found: 60

---

FREE POLYOMINOES:

If we consider the grid of cells as a graph, the problem can be reinterpreted as finding a k-partition of the cells of the grid where each partition has a specific size and in addition each partition is a connected component. I.e. AFAICT there is no difference between a connected component and a polyomino and the rest of this answer makes that assumption.

The finding all possible "k-partitions of the cells of the grid where each partition has a specific size" is pretty trivial to express in the OR-Tools constraint programming. But the connectedness part is hard AFAICT (I tried and failed for quite a while ...). I think OR-Tools constraint programming is not the right approach. I noticed the OR-Tools C++ reference for the network optimization libraries has some stuff on connected components which might be worth a look, but I'm not familiar with it. On the other hand, naive recursive search solution in Python is pretty doable.

Here is a "by hand" naive solution. It's pretty slow but is bearable for your 4x4 case. Addresses are used to identify each cell in the grid. (Also note the wiki page sort of alludes to something like this algorithm as a naive solution and looks like it suggests some more efficient ones for similar polyomino problems).

import numpy as np
from copy import copy
from tabulate import tabulate

D = 4 # Dimension of square grid.
KCC = [5,4,2,2] # List of the sizes of the required k connected components (KCCs).
assert(sum(KCC) <= D*D)
VALID_CELLS = range(2,D*D)

def search():
  solutions = set() # Stash of unique solutions.
  for start in VALID_CELLS: # Try starting search from each possible starting point and expand out.
    marked = np.zeros(D*D).tolist()
    _search(start, marked, set(), solutions, 0, 0)
  for solution in solutions:  # Print results.
    print(tabulate(np.array(solution).reshape(D, D)))
  print('Number of solutions found:', len(solutions))

def _search(i, marked, fringe, solutions, curr_count, curr_part):
  ''' Recursively find each possible KCC in the remaining available cells the find the next, until none left '''
  marked[i] = curr_part+1
  curr_count += 1
  if curr_count == KCC[curr_part]: # If marked K cells for the current CC move onto the next one.
    curr_part += 1
    if curr_part == len(KCC): # If marked K cells and there's no more CCs left we have a solution - not necessarily unique.
      solutions.add(tuple(marked))
    else:
      for start in VALID_CELLS:
        if marked[start] == 0:
          _search(start, copy(marked), set(), solutions, 0, curr_part)
  else:
    fringe.update(neighbours(i, D))
    while(len(fringe)):
      j = fringe.pop()
      if marked[j] == 0:
        _search(j, copy(marked), copy(fringe), solutions, curr_count, curr_part)

def neighbours(i, D):
  ''' Find the address of all cells neighbouring the i-th cell in a DxD grid. '''
  row = int(i/D)
  n = []
  n += [i-1] if int((i-1)/D) == row and (i-1) >= 0 else []
  n += [i+1] if int((i+1)/D) == row and (i+1) < D**2 else []
  n += [i-D] if (i-D) >=0 else []
  n += [i+D] if (i+D) < D**2 else []
  return filter(lambda x: x in VALID_CELLS, n)

if __name__ == '__main__':
  search()

Gives:

...
-  -  -  -
0  0  1  1
2  2  1  1
4  2  3  1
4  2  3  0
-  -  -  -
-  -  -  -
0  0  4  3
1  1  4  3
1  2  2  2
1  1  0  2
-  -  -  -
Number of solutions found: 3884

Aggression

This is very helpful, thank you very much. One thing that is problematic is that your example only works for polyominoes of fixed shapes, the question is about free polyominoes (fixed number of cells but with different shapes, question will be edited for clarity). Following your example, we would have to hard-code every possible shape (+rotations+reflections) for each polyomino of size S... which is not viable. The questions remains, is it possible to implement such constraints with OR-tools ? – Arabele

Oh a missed the "free" part. Hmmm, well the problem can be put "find a 5-partition of a 25-omino where the 25-omino is constrained to a WxH grid, and each the 5 partitions is also X-omino for X = (7,6,6,4,2) ..". I guess it's possible to do in OR-Tools but it smells like it would be easier just to implement CSP back tracking depth first search for this directly: Find possible 25-ominos. For each possible 25-omino do a backtracking CSP search by choosing a X building an X-omino within the 25 domino, until you find a complete solution or have to backtrack. – Aggression

Added something like the naive direct search based solution I alluded to in previous comment for completeness. – Aggression

My apologies for the very late reply. Thank your for your time and for suggesting a recursive approach to this problem. I ended-up implementing Knuth's DLX algorithm for this task, which works relatively well with small inputs. – Arabele

Answer 3

For each polyonomino, and each possible top left cell, you have a boolean variable that indicates if this cell is the top left part of the enclosing rectangle.

For each cell and each polyomino, you have a boolean variable that indicates if this cell is occupied by this polyomino.

Now, for each cell and each polyomino, you have a series of implications: top left cell is selected implies each cell is actually occupied by this polyomino.

Then the constraints: for each cell, at most one polyomino occupies it for each polyomino, there is exactly one cell that is its top left part.

this is a pure boolean problem.

Recension

Thank you so much for the reply ! I honestly have no idea how to implement this with or-tools, is there any example (from the available python examples provided) that you would suggest in particular to help me get started ? – Arabele

I am truly sorry as I am not really understanding your answer. Not sure what "enclosing rectangle" is referring to or how "for each cell and each polyomino" would be translated in code (nested 'for' loop ?). Anyhow, would you mind telling me if your explanation addresses the case of free polyominoes (question has been edited for clarity). – Arabele