The weights enable training a model that is more accurate for certain values of the input (e.g., where the cost of error is higher). Internally, weights w are multiplied by the residuals in the loss function [1]:
![enter image description here]()
Therefore, it is the relative scale of the weights that matters. N can be passed as is if it already reflects the priorities. Uniform scaling would not change the outcome.
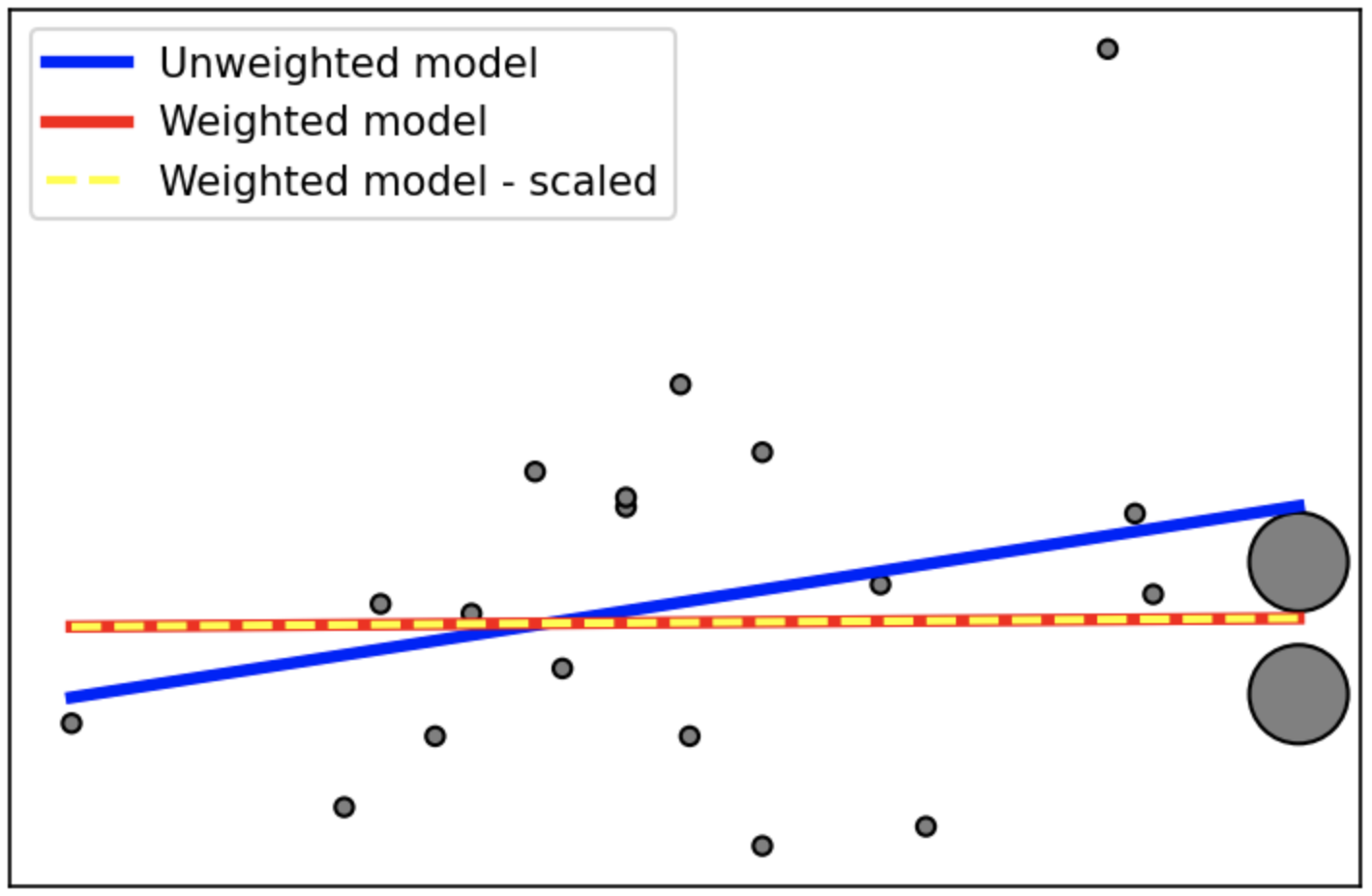
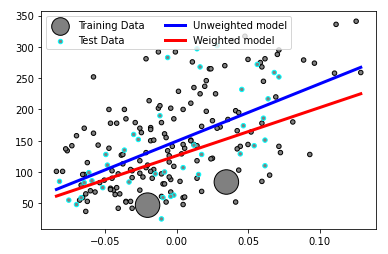
Here is an example. In the weighted version, we emphasize the region around last two samples, and the model becomes more accurate there. And, scaling does not affect the outcome, as expected.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression
# Load the diabetes dataset
X, y = datasets.load_diabetes(return_X_y=True)
n_samples = 20
# Use only one feature and sort
X = X[:, np.newaxis, 2][:n_samples]
y = y[:n_samples]
p = X.argsort(axis=0)
X = X[p].reshape((n_samples, 1))
y = y[p]
# Create equal weights and then augment the last 2 ones
sample_weight = np.ones(n_samples) * 20
sample_weight[-2:] *= 30
plt.scatter(X, y, s=sample_weight, c='grey', edgecolor='black')
# The unweighted model
regr = LinearRegression()
regr.fit(X, y)
plt.plot(X, regr.predict(X), color='blue', linewidth=3, label='Unweighted model')
# The weighted model
regr = LinearRegression()
regr.fit(X, y, sample_weight)
plt.plot(X, regr.predict(X), color='red', linewidth=3, label='Weighted model')
# The weighted model - scaled weights
regr = LinearRegression()
sample_weight = sample_weight / sample_weight.max()
regr.fit(X, y, sample_weight)
plt.plot(X, regr.predict(X), color='yellow', linewidth=2, label='Weighted model - scaled', linestyle='dashed')
plt.xticks(());plt.yticks(());plt.legend();
![enter image description here]()
(this transformation also seems necessary for passing Var1 and Var2 to fit)

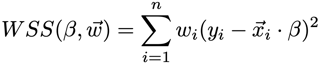
1/N**2as weights, for example). – Pastofitwill make sure of that, but the documentation doesn't mention that, so you'd have to look at the code in scikit-learn to know that. Better cast to float yourself. – Pasto