I want to write a function that takes an array of letters as an argument and a number of those letters to select.
Say you provide an array of 8 letters and want to select 3 letters from that. Then you should get:
8! / ((8 - 3)! * 3!) = 56
Arrays (or words) in return consisting of 3 letters each.
Art of Computer Programming Volume 4: Fascicle 3 has a ton of these that might fit your particular situation better than how I describe.
An issue that you will come across is of course memory and pretty quickly, you'll have problems by 20 elements in your set -- 20C3 = 1140. And if you want to iterate over the set it's best to use a modified gray code algorithm so you aren't holding all of them in memory. These generate the next combination from the previous and avoid repetitions. There are many of these for different uses. Do we want to maximize the differences between successive combinations? minimize? et cetera.
Some of the original papers describing gray codes:
Here are some other papers covering the topic:
Phillip J Chase, `Algorithm 382: Combinations of M out of N Objects' (1970)
You can also reference a combination by its index (in lexicographical order). Realizing that the index should be some amount of change from right to left based on the index we can construct something that should recover a combination.
So, we have a set {1,2,3,4,5,6}... and we want three elements. Let's say {1,2,3} we can say that the difference between the elements is one and in order and minimal. {1,2,4} has one change and is lexicographically number 2. So the number of 'changes' in the last place accounts for one change in the lexicographical ordering. The second place, with one change {1,3,4} has one change but accounts for more change since it's in the second place (proportional to the number of elements in the original set).
The method I've described is a deconstruction, as it seems, from set to the index, we need to do the reverse – which is much trickier. This is how Buckles solves the problem. I wrote some C to compute them, with minor changes – I used the index of the sets rather than a number range to represent the set, so we are always working from 0...n. Note:
There is another way:, its concept is easier to grasp and program but it's without the optimizations of Buckles. Fortunately, it also does not produce duplicate combinations:
The set 
that maximizes 
, where 
.
For an example: 27 = C(6,4) + C(5,3) + C(2,2) + C(1,1). So, the 27th lexicographical combination of four things is: {1,2,5,6}, those are the indexes of whatever set you want to look at. Example below (OCaml), requires choose function, left to reader:
(* this will find the [x] combination of a [set] list when taking [k] elements *)
let combination_maccaffery set k x =
(* maximize function -- maximize a that is aCb *)
(* return largest c where c < i and choose(c,i) <= z *)
let rec maximize a b x =
if (choose a b ) <= x then a else maximize (a-1) b x
in
let rec iterate n x i = match i with
| 0 -> []
| i ->
let max = maximize n i x in
max :: iterate n (x - (choose max i)) (i-1)
in
if x < 0 then failwith "errors" else
let idxs = iterate (List.length set) x k in
List.map (List.nth set) (List.sort (-) idxs)
The following two algorithms are provided for didactic purposes. They implement an iterator and (a more general) folder overall combinations.
They are as fast as possible, having the complexity O(nCk). The memory consumption is bound by k.
We will start with the iterator, which will call a user provided function for each combination
let iter_combs n k f =
let rec iter v s j =
if j = k then f v
else for i = s to n - 1 do iter (i::v) (i+1) (j+1) done in
iter [] 0 0
A more general version will call the user provided function along with the state variable, starting from the initial state. Since we need to pass the state between different states we won't use the for-loop, but instead, use recursion,
let fold_combs n k f x =
let rec loop i s c x =
if i < n then
loop (i+1) s c @@
let c = i::c and s = s + 1 and i = i + 1 in
if s < k then loop i s c x else f c x
else x in
loop 0 0 [] x
In C#:
public static IEnumerable<IEnumerable<T>> Combinations<T>(this IEnumerable<T> elements, int k)
{
return k == 0 ? new[] { new T[0] } :
elements.SelectMany((e, i) =>
elements.Skip(i + 1).Combinations(k - 1).Select(c => (new[] {e}).Concat(c)));
}
Usage:
var result = Combinations(new[] { 1, 2, 3, 4, 5 }, 3);
Result:
123
124
125
134
135
145
234
235
245
345
var result = new[] { 1, 2, 3, 4, 5 }.Combinations(3); –
Aquifer Short java solution:
import java.util.Arrays;
public class Combination {
public static void main(String[] args){
String[] arr = {"A","B","C","D","E","F"};
combinations2(arr, 3, 0, new String[3]);
}
static void combinations2(String[] arr, int len, int startPosition, String[] result){
if (len == 0){
System.out.println(Arrays.toString(result));
return;
}
for (int i = startPosition; i <= arr.length-len; i++){
result[result.length - len] = arr[i];
combinations2(arr, len-1, i+1, result);
}
}
}
Result will be
[A, B, C]
[A, B, D]
[A, B, E]
[A, B, F]
[A, C, D]
[A, C, E]
[A, C, F]
[A, D, E]
[A, D, F]
[A, E, F]
[B, C, D]
[B, C, E]
[B, C, F]
[B, D, E]
[B, D, F]
[B, E, F]
[C, D, E]
[C, D, F]
[C, E, F]
[D, E, F]
May I present my recursive Python solution to this problem?
def choose_iter(elements, length):
for i in xrange(len(elements)):
if length == 1:
yield (elements[i],)
else:
for next in choose_iter(elements[i+1:], length-1):
yield (elements[i],) + next
def choose(l, k):
return list(choose_iter(l, k))
Example usage:
>>> len(list(choose_iter("abcdefgh",3)))
56
I like it for its simplicity.
len(tuple(itertools.combinations('abcdefgh',3))) will achieve the same thing in Python with less code. –
Checkrein for i in xrange(len(elements) - length + 1):? Doesn't matter in python as going out of slice index is handled gracefully but it's the correct algorithm. –
Condiment Lets say your array of letters looks like this: "ABCDEFGH". You have three indices (i, j, k) indicating which letters you are going to use for the current word, You start with:
A B C D E F G H ^ ^ ^ i j k
First you vary k, so the next step looks like that:
A B C D E F G H ^ ^ ^ i j k
If you reached the end you go on and vary j and then k again.
A B C D E F G H ^ ^ ^ i j k A B C D E F G H ^ ^ ^ i j k
Once you j reached G you start also to vary i.
A B C D E F G H ^ ^ ^ i j k A B C D E F G H ^ ^ ^ i j k ...
Written in code this look something like that
void print_combinations(const char *string)
{
int i, j, k;
int len = strlen(string);
for (i = 0; i < len - 2; i++)
{
for (j = i + 1; j < len - 1; j++)
{
for (k = j + 1; k < len; k++)
printf("%c%c%c\n", string[i], string[j], string[k]);
}
}
}
The following recursive algorithm picks all of the k-element combinations from an ordered set:
i of your combinationi with each of the combinations of k-1 elements chosen recursively from the set of elements larger than i.Iterate the above for each i in the set.
It is essential that you pick the rest of the elements as larger than i, to avoid repetition. This way [3,5] will be picked only once, as [3] combined with [5], instead of twice (the condition eliminates [5] + [3]). Without this condition you get variations instead of combinations.
Short example in Python:
def comb(sofar, rest, n):
if n == 0:
print sofar
else:
for i in range(len(rest)):
comb(sofar + rest[i], rest[i+1:], n-1)
>>> comb("", "abcde", 3)
abc
abd
abe
acd
ace
ade
bcd
bce
bde
cde
For explanation, the recursive method is described with the following example:
Example: A B C D E
All combinations of 3 would be:
I found this thread useful and thought I would add a Javascript solution that you can pop into Firebug. Depending on your JS engine, it could take a little time if the starting string is large.
function string_recurse(active, rest) {
if (rest.length == 0) {
console.log(active);
} else {
string_recurse(active + rest.charAt(0), rest.substring(1, rest.length));
string_recurse(active, rest.substring(1, rest.length));
}
}
string_recurse("", "abc");
The output should be as follows:
abc
ab
ac
a
bc
b
c
In C++ the following routine will produce all combinations of length distance(first,k) between the range [first,last):
#include <algorithm>
template <typename Iterator>
bool next_combination(const Iterator first, Iterator k, const Iterator last)
{
/* Credits: Mark Nelson http://marknelson.us */
if ((first == last) || (first == k) || (last == k))
return false;
Iterator i1 = first;
Iterator i2 = last;
++i1;
if (last == i1)
return false;
i1 = last;
--i1;
i1 = k;
--i2;
while (first != i1)
{
if (*--i1 < *i2)
{
Iterator j = k;
while (!(*i1 < *j)) ++j;
std::iter_swap(i1,j);
++i1;
++j;
i2 = k;
std::rotate(i1,j,last);
while (last != j)
{
++j;
++i2;
}
std::rotate(k,i2,last);
return true;
}
}
std::rotate(first,k,last);
return false;
}
It can be used like this:
#include <string>
#include <iostream>
int main()
{
std::string s = "12345";
std::size_t comb_size = 3;
do
{
std::cout << std::string(s.begin(), s.begin() + comb_size) << std::endl;
} while (next_combination(s.begin(), s.begin() + comb_size, s.end()));
return 0;
}
This will print the following:
123
124
125
134
135
145
234
235
245
345
being and begin with s.begin(), and end with s.end(). The code closely follows STL's next_permutation algorithm, described here in more details. –
Polysemy Simple recursive algorithm in Haskell
import Data.List
combinations 0 lst = [[]]
combinations n lst = do
(x:xs) <- tails lst
rest <- combinations (n-1) xs
return $ x : rest
We first define the special case, i.e. selecting zero elements. It produces a single result, which is an empty list (i.e. a list that contains an empty list).
For n > 0, x goes through every element of the list and xs is every element after x.
rest picks n - 1 elements from xs using a recursive call to combinations. The final result of the function is a list where each element is x : rest (i.e. a list which has x as head and rest as tail) for every different value of x and rest.
> combinations 3 "abcde"
["abc","abd","abe","acd","ace","ade","bcd","bce","bde","cde"]
And of course, since Haskell is lazy, the list is gradually generated as needed, so you can partially evaluate exponentially large combinations.
> let c = combinations 8 "abcdefghijklmnopqrstuvwxyz"
> take 10 c
["abcdefgh","abcdefgi","abcdefgj","abcdefgk","abcdefgl","abcdefgm","abcdefgn",
"abcdefgo","abcdefgp","abcdefgq"]
static IEnumerable<string> Combinations(List<string> characters, int length)
{
for (int i = 0; i < characters.Count; i++)
{
// only want 1 character, just return this one
if (length == 1)
yield return characters[i];
// want more than one character, return this one plus all combinations one shorter
// only use characters after the current one for the rest of the combinations
else
foreach (string next in Combinations(characters.GetRange(i + 1, characters.Count - (i + 1)), length - 1))
yield return characters[i] + next;
}
}
And here comes granddaddy COBOL, the much maligned language.
Let's assume an array of 34 elements of 8 bytes each (purely arbitrary selection.) The idea is to enumerate all possible 4-element combinations and load them into an array.
We use 4 indices, one each for each position in the group of 4
The array is processed like this:
idx1 = 1
idx2 = 2
idx3 = 3
idx4 = 4
We vary idx4 from 4 to the end. For each idx4 we get a unique combination of groups of four. When idx4 comes to the end of the array, we increment idx3 by 1 and set idx4 to idx3+1. Then we run idx4 to the end again. We proceed in this manner, augmenting idx3,idx2, and idx1 respectively until the position of idx1 is less than 4 from the end of the array. That finishes the algorithm.
1 --- pos.1
2 --- pos 2
3 --- pos 3
4 --- pos 4
5
6
7
etc.
First iterations:
1234
1235
1236
1237
1245
1246
1247
1256
1257
1267
etc.
A COBOL example:
01 DATA_ARAY.
05 FILLER PIC X(8) VALUE "VALUE_01".
05 FILLER PIC X(8) VALUE "VALUE_02".
etc.
01 ARAY_DATA OCCURS 34.
05 ARAY_ITEM PIC X(8).
01 OUTPUT_ARAY OCCURS 50000 PIC X(32).
01 MAX_NUM PIC 99 COMP VALUE 34.
01 INDEXXES COMP.
05 IDX1 PIC 99.
05 IDX2 PIC 99.
05 IDX3 PIC 99.
05 IDX4 PIC 99.
05 OUT_IDX PIC 9(9).
01 WHERE_TO_STOP_SEARCH PIC 99 COMP.
* Stop the search when IDX1 is on the third last array element:
COMPUTE WHERE_TO_STOP_SEARCH = MAX_VALUE - 3
MOVE 1 TO IDX1
PERFORM UNTIL IDX1 > WHERE_TO_STOP_SEARCH
COMPUTE IDX2 = IDX1 + 1
PERFORM UNTIL IDX2 > MAX_NUM
COMPUTE IDX3 = IDX2 + 1
PERFORM UNTIL IDX3 > MAX_NUM
COMPUTE IDX4 = IDX3 + 1
PERFORM UNTIL IDX4 > MAX_NUM
ADD 1 TO OUT_IDX
STRING ARAY_ITEM(IDX1)
ARAY_ITEM(IDX2)
ARAY_ITEM(IDX3)
ARAY_ITEM(IDX4)
INTO OUTPUT_ARAY(OUT_IDX)
ADD 1 TO IDX4
END-PERFORM
ADD 1 TO IDX3
END-PERFORM
ADD 1 TO IDX2
END_PERFORM
ADD 1 TO IDX1
END-PERFORM.
Another C# version with lazy generation of the combination indices. This version maintains a single array of indices to define a mapping between the list of all values and the values for the current combination, i.e. constantly uses O(k) additional space during the entire runtime. The code generates individual combinations, including the first one, in O(k) time.
public static IEnumerable<T[]> Combinations<T>(this T[] values, int k)
{
if (k < 0 || values.Length < k)
yield break; // invalid parameters, no combinations possible
// generate the initial combination indices
var combIndices = new int[k];
for (var i = 0; i < k; i++)
{
combIndices[i] = i;
}
while (true)
{
// return next combination
var combination = new T[k];
for (var i = 0; i < k; i++)
{
combination[i] = values[combIndices[i]];
}
yield return combination;
// find first index to update
var indexToUpdate = k - 1;
while (indexToUpdate >= 0 && combIndices[indexToUpdate] >= values.Length - k + indexToUpdate)
{
indexToUpdate--;
}
if (indexToUpdate < 0)
yield break; // done
// update combination indices
for (var combIndex = combIndices[indexToUpdate] + 1; indexToUpdate < k; indexToUpdate++, combIndex++)
{
combIndices[indexToUpdate] = combIndex;
}
}
}
Test code:
foreach (var combination in new[] {'a', 'b', 'c', 'd', 'e'}.Combinations(3))
{
System.Console.WriteLine(String.Join(" ", combination));
}
Output:
a b c
a b d
a b e
a c d
a c e
a d e
b c d
b c e
b d e
c d e
c b a which it does not. –
Hardiness If you can use SQL syntax - say, if you're using LINQ to access fields of an structure or array, or directly accessing a database that has a table called "Alphabet" with just one char field "Letter", you can adapt following code:
SELECT A.Letter, B.Letter, C.Letter
FROM Alphabet AS A, Alphabet AS B, Alphabet AS C
WHERE A.Letter<>B.Letter AND A.Letter<>C.Letter AND B.Letter<>C.Letter
AND A.Letter<B.Letter AND B.Letter<C.Letter
This will return all combinations of 3 letters, notwithstanding how many letters you have in table "Alphabet" (it can be 3, 8, 10, 27, etc.).
If what you want is all permutations, rather than combinations (i.e. you want "ACB" and "ABC" to count as different, rather than appear just once) just delete the last line (the AND one) and it's done.
Post-Edit: After re-reading the question, I realise what's needed is the general algorithm, not just a specific one for the case of selecting 3 items. Adam Hughes' answer is the complete one, unfortunately I cannot vote it up (yet). This answer's simple but works only for when you want exactly 3 items.
Here is an elegant, generic implementation in Scala, as described on 99 Scala Problems.
object P26 {
def flatMapSublists[A,B](ls: List[A])(f: (List[A]) => List[B]): List[B] =
ls match {
case Nil => Nil
case sublist@(_ :: tail) => f(sublist) ::: flatMapSublists(tail)(f)
}
def combinations[A](n: Int, ls: List[A]): List[List[A]] =
if (n == 0) List(Nil)
else flatMapSublists(ls) { sl =>
combinations(n - 1, sl.tail) map {sl.head :: _}
}
}
I had a permutation algorithm I used for project euler, in python:
def missing(miss,src):
"Returns the list of items in src not present in miss"
return [i for i in src if i not in miss]
def permutation_gen(n,l):
"Generates all the permutations of n items of the l list"
for i in l:
if n<=1: yield [i]
r = [i]
for j in permutation_gen(n-1,missing([i],l)): yield r+j
If
n<len(l)
you should have all combination you need without repetition, do you need it?
It is a generator, so you use it in something like this:
for comb in permutation_gen(3,list("ABCDEFGH")):
print comb
Lets say your array of letters looks like this: "ABCDEFGH". You have three indices (i, j, k) indicating which letters you are going to use for the current word, You start with:
A B C D E F G H ^ ^ ^ i j k
First you vary k, so the next step looks like that:
A B C D E F G H ^ ^ ^ i j k
If you reached the end you go on and vary j and then k again.
A B C D E F G H ^ ^ ^ i j k A B C D E F G H ^ ^ ^ i j k
Once you j reached G you start also to vary i.
A B C D E F G H ^ ^ ^ i j k A B C D E F G H ^ ^ ^ i j k ...
function initializePointers($cnt) {
$pointers = [];
for($i=0; $i<$cnt; $i++) {
$pointers[] = $i;
}
return $pointers;
}
function incrementPointers(&$pointers, &$arrLength) {
for($i=0; $i<count($pointers); $i++) {
$currentPointerIndex = count($pointers) - $i - 1;
$currentPointer = $pointers[$currentPointerIndex];
if($currentPointer < $arrLength - $i - 1) {
++$pointers[$currentPointerIndex];
for($j=1; ($currentPointerIndex+$j)<count($pointers); $j++) {
$pointers[$currentPointerIndex+$j] = $pointers[$currentPointerIndex]+$j;
}
return true;
}
}
return false;
}
function getDataByPointers(&$arr, &$pointers) {
$data = [];
for($i=0; $i<count($pointers); $i++) {
$data[] = $arr[$pointers[$i]];
}
return $data;
}
function getCombinations($arr, $cnt)
{
$len = count($arr);
$result = [];
$pointers = initializePointers($cnt);
do {
$result[] = getDataByPointers($arr, $pointers);
} while(incrementPointers($pointers, count($arr)));
return $result;
}
$result = getCombinations([0, 1, 2, 3, 4, 5], 3);
print_r($result);
Based on https://mcmap.net/q/63883/-algorithm-to-return-all-combinations-of-k-elements-from-n, but more abstract, for any size of pointers.
https://gist.github.com/3118596
There is an implementation for JavaScript. It has functions to get k-combinations and all combinations of an array of any objects. Examples:
k_combinations([1,2,3], 2)
-> [[1,2], [1,3], [2,3]]
combinations([1,2,3])
-> [[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3]]
Here you have a lazy evaluated version of that algorithm coded in C#:
static bool nextCombination(int[] num, int n, int k)
{
bool finished, changed;
changed = finished = false;
if (k > 0)
{
for (int i = k - 1; !finished && !changed; i--)
{
if (num[i] < (n - 1) - (k - 1) + i)
{
num[i]++;
if (i < k - 1)
{
for (int j = i + 1; j < k; j++)
{
num[j] = num[j - 1] + 1;
}
}
changed = true;
}
finished = (i == 0);
}
}
return changed;
}
static IEnumerable Combinations<T>(IEnumerable<T> elements, int k)
{
T[] elem = elements.ToArray();
int size = elem.Length;
if (k <= size)
{
int[] numbers = new int[k];
for (int i = 0; i < k; i++)
{
numbers[i] = i;
}
do
{
yield return numbers.Select(n => elem[n]);
}
while (nextCombination(numbers, size, k));
}
}
And test part:
static void Main(string[] args)
{
int k = 3;
var t = new[] { "dog", "cat", "mouse", "zebra"};
foreach (IEnumerable<string> i in Combinations(t, k))
{
Console.WriteLine(string.Join(",", i));
}
}
Hope this help you!
Another version, that forces all the first k to appear firstly, then all the first k+1 combinations, then all the first k+2 etc.. It means that if you have sorted array, the most important on the top, it would take them and expand gradually to the next ones - only when it is must do so.
private static bool NextCombinationFirstsAlwaysFirst(int[] num, int n, int k)
{
if (k > 1 && NextCombinationFirstsAlwaysFirst(num, num[k - 1], k - 1))
return true;
if (num[k - 1] + 1 == n)
return false;
++num[k - 1];
for (int i = 0; i < k - 1; ++i)
num[i] = i;
return true;
}
For instance, if you run the first method ("nextCombination") on k=3, n=5 you'll get:
0 1 2
0 1 3
0 1 4
0 2 3
0 2 4
0 3 4
1 2 3
1 2 4
1 3 4
2 3 4
But if you'll run
int[] nums = new int[k];
for (int i = 0; i < k; ++i)
nums[i] = i;
do
{
Console.WriteLine(string.Join(" ", nums));
}
while (NextCombinationFirstsAlwaysFirst(nums, n, k));
You'll get this (I added empty lines for clarity):
0 1 2
0 1 3
0 2 3
1 2 3
0 1 4
0 2 4
1 2 4
0 3 4
1 3 4
2 3 4
It's adding "4" only when must to, and also after "4" was added it adds "3" again only when it must to (after doing 01, 02, 12).
Algorithm:
In C#:
void Main()
{
var set = new [] {"A", "B", "C", "D" }; //, "E", "F", "G", "H", "I", "J" };
var kElement = 2;
for(var i = 1; i < Math.Pow(2, set.Length); i++) {
var result = Convert.ToString(i, 2).PadLeft(set.Length, '0');
var cnt = Regex.Matches(Regex.Escape(result), "1").Count;
if (cnt == kElement) {
for(int j = 0; j < set.Length; j++)
if ( Char.GetNumericValue(result[j]) == 1)
Console.Write(set[j]);
Console.WriteLine();
}
}
}
Why does it work?
There is a bijection between the subsets of an n-element set and n-bit sequences.
That means we can figure out how many subsets there are by counting sequences.
e.g., the four element set below can be represented by {0,1} X {0, 1} X {0, 1} X {0, 1} (or 2^4) different sequences.
So - all we have to do is count from 1 to 2^n to find all the combinations. (We ignore the empty set.) Next, translate the digits to their binary representation. Then substitute elements of your set for 'on' bits.
If you want only k element results, only print when k bits are 'on'.
(If you want all subsets instead of k length subsets, remove the cnt/kElement part.)
For proof, see MIT free courseware Mathematics for Computer Science, Lehman et al, section 11.2.2.
var cnt = System.Runtime.Intrinsics.X86.Popcnt.PopCount(i); –
Fusain short python code, yielding index positions
def yield_combos(n,k):
# n is set size, k is combo size
i = 0
a = [0]*k
while i > -1:
for j in range(i+1, k):
a[j] = a[j-1]+1
i=j
yield a
while a[i] == i + n - k:
i -= 1
a[i] += 1
Clojure version:
(defn comb [k l]
(if (= 1 k) (map vector l)
(apply concat
(map-indexed
#(map (fn [x] (conj x %2))
(comb (dec k) (drop (inc %1) l)))
l))))
Array.prototype.combs = function(num) {
var str = this,
length = str.length,
of = Math.pow(2, length) - 1,
out, combinations = [];
while(of) {
out = [];
for(var i = 0, y; i < length; i++) {
y = (1 << i);
if(y & of && (y !== of))
out.push(str[i]);
}
if (out.length >= num) {
combinations.push(out);
}
of--;
}
return combinations;
}
Another python recusive solution.
def combination_indicies(n, k, j = 0, stack = []):
if len(stack) == k:
yield list(stack)
return
for i in range(j, n):
stack.append(i)
for x in combination_indicies(n, k, i + 1, stack):
yield x
stack.pop()
list(combination_indicies(5, 3))
Output:
[[0, 1, 2],
[0, 1, 3],
[0, 1, 4],
[0, 2, 3],
[0, 2, 4],
[0, 3, 4],
[1, 2, 3],
[1, 2, 4],
[1, 3, 4],
[2, 3, 4]]
Short javascript version (ES 5)
let combine = (list, n) =>
n == 0 ?
[[]] :
list.flatMap((e, i) =>
combine(
list.slice(i + 1),
n - 1
).map(c => [e].concat(c))
);
let res = combine([1,2,3,4], 3);
res.forEach(e => console.log(e.join()));All said and and done here comes the O'caml code for that. Algorithm is evident from the code..
let combi n lst =
let rec comb l c =
if( List.length c = n) then [c] else
match l with
[] -> []
| (h::t) -> (combi t (h::c))@(combi t c)
in
combi lst []
;;
Here is a method which gives you all combinations of specified size from a random length string. Similar to quinmars' solution, but works for varied input and k.
The code can be changed to wrap around, ie 'dab' from input 'abcd' w k=3.
public void run(String data, int howMany){
choose(data, howMany, new StringBuffer(), 0);
}
//n choose k
private void choose(String data, int k, StringBuffer result, int startIndex){
if (result.length()==k){
System.out.println(result.toString());
return;
}
for (int i=startIndex; i<data.length(); i++){
result.append(data.charAt(i));
choose(data,k,result, i+1);
result.setLength(result.length()-1);
}
}
Output for "abcde":
abc abd abe acd ace ade bcd bce bde cde
A concise Javascript solution:
Array.prototype.combine=function combine(k){
var toCombine=this;
var last;
function combi(n,comb){
var combs=[];
for ( var x=0,y=comb.length;x<y;x++){
for ( var l=0,m=toCombine.length;l<m;l++){
combs.push(comb[x]+toCombine[l]);
}
}
if (n<k-1){
n++;
combi(n,combs);
} else{last=combs;}
}
combi(1,toCombine);
return last;
}
// Example:
// var toCombine=['a','b','c'];
// var results=toCombine.combine(4);
combi(1,toCombine); to combi(0, ['']);, this solution works for k=1. As written, calling with k=1 gives the same results as k=2. –
Mediator Here is a code I recently wrote in Java, which calculates and returns all the combination of "num" elements from "outOf" elements.
// author: Sourabh Bhat ([email protected])
public class Testing
{
public static void main(String[] args)
{
// Test case num = 5, outOf = 8.
int num = 5;
int outOf = 8;
int[][] combinations = getCombinations(num, outOf);
for (int i = 0; i < combinations.length; i++)
{
for (int j = 0; j < combinations[i].length; j++)
{
System.out.print(combinations[i][j] + " ");
}
System.out.println();
}
}
private static int[][] getCombinations(int num, int outOf)
{
int possibilities = get_nCr(outOf, num);
int[][] combinations = new int[possibilities][num];
int arrayPointer = 0;
int[] counter = new int[num];
for (int i = 0; i < num; i++)
{
counter[i] = i;
}
breakLoop: while (true)
{
// Initializing part
for (int i = 1; i < num; i++)
{
if (counter[i] >= outOf - (num - 1 - i))
counter[i] = counter[i - 1] + 1;
}
// Testing part
for (int i = 0; i < num; i++)
{
if (counter[i] < outOf)
{
continue;
} else
{
break breakLoop;
}
}
// Innermost part
combinations[arrayPointer] = counter.clone();
arrayPointer++;
// Incrementing part
counter[num - 1]++;
for (int i = num - 1; i >= 1; i--)
{
if (counter[i] >= outOf - (num - 1 - i))
counter[i - 1]++;
}
}
return combinations;
}
private static int get_nCr(int n, int r)
{
if(r > n)
{
throw new ArithmeticException("r is greater then n");
}
long numerator = 1;
long denominator = 1;
for (int i = n; i >= r + 1; i--)
{
numerator *= i;
}
for (int i = 2; i <= n - r; i++)
{
denominator *= i;
}
return (int) (numerator / denominator);
}
}
I created a solution in SQL Server 2005 for this, and posted it on my website: http://www.jessemclain.com/downloads/code/sql/fn_GetMChooseNCombos.sql.htm
Here is an example to show usage:
SELECT * FROM dbo.fn_GetMChooseNCombos('ABCD', 2, '')
results:
Word
----
AB
AC
AD
BC
BD
CD
(6 row(s) affected)
Here is my proposition in C++
I tried to impose as little restriction on the iterator type as i could so this solution assumes just forward iterator, and it can be a const_iterator. This should work with any standard container. In cases where arguments don't make sense it throws std::invalid_argumnent
#include <vector>
#include <stdexcept>
template <typename Fci> // Fci - forward const iterator
std::vector<std::vector<Fci> >
enumerate_combinations(Fci begin, Fci end, unsigned int combination_size)
{
if(begin == end && combination_size > 0u)
throw std::invalid_argument("empty set and positive combination size!");
std::vector<std::vector<Fci> > result; // empty set of combinations
if(combination_size == 0u) return result; // there is exactly one combination of
// size 0 - emty set
std::vector<Fci> current_combination;
current_combination.reserve(combination_size + 1u); // I reserve one aditional slot
// in my vector to store
// the end sentinel there.
// The code is cleaner thanks to that
for(unsigned int i = 0u; i < combination_size && begin != end; ++i, ++begin)
{
current_combination.push_back(begin); // Construction of the first combination
}
// Since I assume the itarators support only incrementing, I have to iterate over
// the set to get its size, which is expensive. Here I had to itrate anyway to
// produce the first cobination, so I use the loop to also check the size.
if(current_combination.size() < combination_size)
throw std::invalid_argument("combination size > set size!");
result.push_back(current_combination); // Store the first combination in the results set
current_combination.push_back(end); // Here I add mentioned earlier sentinel to
// simplyfy rest of the code. If I did it
// earlier, previous statement would get ugly.
while(true)
{
unsigned int i = combination_size;
Fci tmp; // Thanks to the sentinel I can find first
do // iterator to change, simply by scaning
{ // from right to left and looking for the
tmp = current_combination[--i]; // first "bubble". The fact, that it's
++tmp; // a forward iterator makes it ugly but I
} // can't help it.
while(i > 0u && tmp == current_combination[i + 1u]);
// Here is probably my most obfuscated expression.
// Loop above looks for a "bubble". If there is no "bubble", that means, that
// current_combination is the last combination, Expression in the if statement
// below evaluates to true and the function exits returning result.
// If the "bubble" is found however, the ststement below has a sideeffect of
// incrementing the first iterator to the left of the "bubble".
if(++current_combination[i] == current_combination[i + 1u])
return result;
// Rest of the code sets posiotons of the rest of the iterstors
// (if there are any), that are to the right of the incremented one,
// to form next combination
while(++i < combination_size)
{
current_combination[i] = current_combination[i - 1u];
++current_combination[i];
}
// Below is the ugly side of using the sentinel. Well it had to haave some
// disadvantage. Try without it.
result.push_back(std::vector<Fci>(current_combination.begin(),
current_combination.end() - 1));
}
}
JavaScript, generator-based, recursive approach:
function *nCk(n,k){
for(var i=n-1;i>=k-1;--i)
if(k===1)
yield [i];
else
for(var temp of nCk(i,k-1)){
temp.unshift(i);
yield temp;
}
}
function test(){
try{
var n=parseInt(ninp.value);
var k=parseInt(kinp.value);
log.innerText="";
var stop=Date.now()+1000;
if(k>=1)
for(var res of nCk(n,k))
if(Date.now()<stop)
log.innerText+=JSON.stringify(res)+" ";
else{
log.innerText+="1 second passed, stopping here.";
break;
}
}catch(ex){}
}n:<input id="ninp" oninput="test()">
>= k:<input id="kinp" oninput="test()"> >= 1
<div id="log"></div>This way (decreasing i and unshift()) it produces combinations and elements inside combinations in decreasing order, somewhat pleasing the eye.
Test stops after 1 second, so entering weird numbers is relatively safe.
Jumping on the bandwagon, and posting another solution. This is a generic Java implementation. Input: (int k) is number of elements to choose and (List<T> list) is the list to choose from. Returns a list of combinations (List<List<T>>).
public static <T> List<List<T>> getCombinations(int k, List<T> list) {
List<List<T>> combinations = new ArrayList<List<T>>();
if (k == 0) {
combinations.add(new ArrayList<T>());
return combinations;
}
for (int i = 0; i < list.size(); i++) {
T element = list.get(i);
List<T> rest = getSublist(list, i+1);
for (List<T> previous : getCombinations(k-1, rest)) {
previous.add(element);
combinations.add(previous);
}
}
return combinations;
}
public static <T> List<T> getSublist(List<T> list, int i) {
List<T> sublist = new ArrayList<T>();
for (int j = i; j < list.size(); j++) {
sublist.add(list.get(j));
}
return sublist;
}
C code for Algorithm L (Lexicographic combinations) in Section 7.2.1.3 of The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 :
#include <stdio.h>
#include <stdlib.h>
void visit(int* c, int t)
{
// for (int j = 1; j <= t; j++)
for (int j = t; j > 0; j--)
printf("%d ", c[j]);
printf("\n");
}
int* initialize(int n, int t)
{
// c[0] not used
int *c = (int*) malloc((t + 3) * sizeof(int));
for (int j = 1; j <= t; j++)
c[j] = j - 1;
c[t+1] = n;
c[t+2] = 0;
return c;
}
void comb(int n, int t)
{
int *c = initialize(n, t);
int j;
for (;;) {
visit(c, t);
j = 1;
while (c[j]+1 == c[j+1]) {
c[j] = j - 1;
++j;
}
if (j > t)
return;
++c[j];
}
free(c);
}
int main(int argc, char *argv[])
{
comb(5, 3);
return 0;
}
Here's my JavaScript solution that is a little more functional through use of reduce/map, which eliminates almost all variables
function combinations(arr, size) {
var len = arr.length;
if (size > len) return [];
if (!size) return [[]];
if (size == len) return [arr];
return arr.reduce(function (acc, val, i) {
var res = combinations(arr.slice(i + 1), size - 1)
.map(function (comb) { return [val].concat(comb); });
return acc.concat(res);
}, []);
}
var combs = combinations([1,2,3,4,5,6,7,8],3);
combs.map(function (comb) {
document.body.innerHTML += comb.toString() + '<br />';
});
document.body.innerHTML += '<br /> Total combinations = ' + combs.length;Short php algorithm to return all combinations of k elements from n (binomial coefficent) based on java solution:
$array = array(1,2,3,4,5);
$array_result = NULL;
$array_general = NULL;
function combinations($array, $len, $start_position, $result_array, $result_len, &$general_array)
{
if($len == 0)
{
$general_array[] = $result_array;
return;
}
for ($i = $start_position; $i <= count($array) - $len; $i++)
{
$result_array[$result_len - $len] = $array[$i];
combinations($array, $len-1, $i+1, $result_array, $result_len, $general_array);
}
}
combinations($array, 3, 0, $array_result, 3, $array_general);
echo "<pre>";
print_r($array_general);
echo "</pre>";
The same solution but in javascript:
var newArray = [1, 2, 3, 4, 5];
var arrayResult = [];
var arrayGeneral = [];
function combinations(newArray, len, startPosition, resultArray, resultLen, arrayGeneral) {
if(len === 0) {
var tempArray = [];
resultArray.forEach(value => tempArray.push(value));
arrayGeneral.push(tempArray);
return;
}
for (var i = startPosition; i <= newArray.length - len; i++) {
resultArray[resultLen - len] = newArray[i];
combinations(newArray, len-1, i+1, resultArray, resultLen, arrayGeneral);
}
}
combinations(newArray, 3, 0, arrayResult, 3, arrayGeneral);
console.log(arrayGeneral);
$array, $len, $start_position, $result_array, $result_len, &$general_array for? –
Insignificance I have written a class to handle common functions for working with the binomial coefficient, which is the type of problem that your problem falls under. It performs the following tasks:
Outputs all the K-indexes in a nice format for any N choose K to a file. The K-indexes can be substituted with more descriptive strings or letters. This method makes solving this type of problem quite trivial.
Converts the K-indexes to the proper index of an entry in the sorted binomial coefficient table. This technique is much faster than older published techniques that rely on iteration. It does this by using a mathematical property inherent in Pascal's Triangle. My paper talks about this. I believe I am the first to discover and publish this technique, but I could be wrong.
Converts the index in a sorted binomial coefficient table to the corresponding K-indexes.
Uses Mark Dominus method to calculate the binomial coefficient, which is much less likely to overflow and works with larger numbers.
The class is written in .NET C# and provides a way to manage the objects related to the problem (if any) by using a generic list. The constructor of this class takes a bool value called InitTable that when true will create a generic list to hold the objects to be managed. If this value is false, then it will not create the table. The table does not need to be created in order to perform the 4 above methods. Accessor methods are provided to access the table.
There is an associated test class which shows how to use the class and its methods. It has been extensively tested with 2 cases and there are no known bugs.
To read about this class and download the code, see Tablizing The Binomial Coeffieicent.
It should not be hard to convert this class to C++.
Following Haskell code calculate the combination number and combinations at the same time, and thanks to Haskell's laziness, you can get one part of them without calculating the other.
import Data.Semigroup
import Data.Monoid
data Comb = MkComb {count :: Int, combinations :: [[Int]]} deriving (Show, Eq, Ord)
instance Semigroup Comb where
(MkComb c1 cs1) <> (MkComb c2 cs2) = MkComb (c1 + c2) (cs1 ++ cs2)
instance Monoid Comb where
mempty = MkComb 0 []
addElem :: Comb -> Int -> Comb
addElem (MkComb c cs) x = MkComb c (map (x :) cs)
comb :: Int -> Int -> Comb
comb n k | n < 0 || k < 0 = error "error in `comb n k`, n and k should be natural number"
comb n k | k == 0 || k == n = MkComb 1 [(take k [k-1,k-2..0])]
comb n k | n < k = mempty
comb n k = comb (n-1) k <> (comb (n-1) (k-1) `addElem` (n-1))
It works like:
*Main> comb 0 1
MkComb {count = 0, combinations = []}
*Main> comb 0 0
MkComb {count = 1, combinations = [[]]}
*Main> comb 1 1
MkComb {count = 1, combinations = [[0]]}
*Main> comb 4 2
MkComb {count = 6, combinations = [[1,0],[2,0],[2,1],[3,0],[3,1],[3,2]]}
*Main> count (comb 10 5)
252
Here is a Lisp approach using a macro. This works in Common Lisp and should work in other Lisp dialects.
The code below creates 'n' nested loops and executes an arbitrary chunk of code (stored in the body variable) for each combination of 'n' elements from the list lst. The variable var points to a list containing the variables used for the loops.
(defmacro do-combinations ((var lst num) &body body)
(loop with syms = (loop repeat num collect (gensym))
for i on syms
for k = `(loop for ,(car i) on (cdr ,(cadr i))
do (let ((,var (list ,@(reverse syms)))) (progn ,@body)))
then `(loop for ,(car i) on ,(if (cadr i) `(cdr ,(cadr i)) lst) do ,k)
finally (return k)))
Let's see...
(macroexpand-1 '(do-combinations (p '(1 2 3 4 5 6 7) 4) (pprint (mapcar #'car p))))
(LOOP FOR #:G3217 ON '(1 2 3 4 5 6 7) DO
(LOOP FOR #:G3216 ON (CDR #:G3217) DO
(LOOP FOR #:G3215 ON (CDR #:G3216) DO
(LOOP FOR #:G3214 ON (CDR #:G3215) DO
(LET ((P (LIST #:G3217 #:G3216 #:G3215 #:G3214)))
(PROGN (PPRINT (MAPCAR #'CAR P))))))))
(do-combinations (p '(1 2 3 4 5 6 7) 4) (pprint (mapcar #'car p)))
(1 2 3 4)
(1 2 3 5)
(1 2 3 6)
...
Since combinations are not stored by default, storage is kept to a minimum. The possibility of choosing the body code instead of storing all results also affords more flexibility.
We can use the concept of bits to do this. Let we have a string of "abc," and we want to have all combinations of the elements with length 2 (i.e "ab" , "ac","bc".)
We can find the set bits in numbers ranging from 1 to 2^n (exclusive). Here 1 to 7, and wherever we have set bits = 2, we can print the corresponding value from string.
for example:
print ab (str[0] , str[1])print ac (str[0] , str[2])print ab (str[1] , str[2])
Code sample:
public class StringCombinationK {
static void combk(String s , int k){
int n = s.length();
int num = 1<<n;
int j=0;
int count=0;
for(int i=0;i<num;i++){
if (countSet(i)==k){
setBits(i,j,s);
count++;
System.out.println();
}
}
System.out.println(count);
}
static void setBits(int i,int j,String s){ // print the corresponding string value,j represent the index of set bit
if(i==0){
return;
}
if(i%2==1){
System.out.print(s.charAt(j));
}
setBits(i/2,j+1,s);
}
static int countSet(int i){ //count number of set bits
if( i==0){
return 0;
}
return (i%2==0? 0:1) + countSet(i/2);
}
public static void main(String[] arhs){
String s = "abcdefgh";
int k=3;
combk(s,k);
}
}
Another one solution with C#:
static List<List<T>> GetCombinations<T>(List<T> originalItems, int combinationLength)
{
if (combinationLength < 1)
{
return null;
}
return CreateCombinations<T>(new List<T>(), 0, combinationLength, originalItems);
}
static List<List<T>> CreateCombinations<T>(List<T> initialCombination, int startIndex, int length, List<T> originalItems)
{
List<List<T>> combinations = new List<List<T>>();
for (int i = startIndex; i < originalItems.Count - length + 1; i++)
{
List<T> newCombination = new List<T>(initialCombination);
newCombination.Add(originalItems[i]);
if (length > 1)
{
List<List<T>> newCombinations = CreateCombinations(newCombination, i + 1, length - 1, originalItems);
combinations.AddRange(newCombinations);
}
else
{
combinations.Add(newCombination);
}
}
return combinations;
}
Example of usage:
List<char> initialArray = new List<char>() { 'a','b','c','d'};
int combinationLength = 3;
List<List<char>> combinations = GetCombinations(initialArray, combinationLength);
I was looking for a similar solution for PHP and came across the following
class Combinations implements Iterator
{
protected $c = null;
protected $s = null;
protected $n = 0;
protected $k = 0;
protected $pos = 0;
function __construct($s, $k) {
if(is_array($s)) {
$this->s = array_values($s);
$this->n = count($this->s);
} else {
$this->s = (string) $s;
$this->n = strlen($this->s);
}
$this->k = $k;
$this->rewind();
}
function key() {
return $this->pos;
}
function current() {
$r = array();
for($i = 0; $i < $this->k; $i++)
$r[] = $this->s[$this->c[$i]];
return is_array($this->s) ? $r : implode('', $r);
}
function next() {
if($this->_next())
$this->pos++;
else
$this->pos = -1;
}
function rewind() {
$this->c = range(0, $this->k);
$this->pos = 0;
}
function valid() {
return $this->pos >= 0;
}
protected function _next() {
$i = $this->k - 1;
while ($i >= 0 && $this->c[$i] == $this->n - $this->k + $i)
$i--;
if($i < 0)
return false;
$this->c[$i]++;
while($i++ < $this->k - 1)
$this->c[$i] = $this->c[$i - 1] + 1;
return true;
}
}
foreach(new Combinations("1234567", 5) as $substring)
echo $substring, ' ';
I'm not to sure how efficient the class is, but I was only using it for a seeder.
#include <stdio.h>
unsigned int next_combination(unsigned int *ar, size_t n, unsigned int k)
{
unsigned int finished = 0;
unsigned int changed = 0;
unsigned int i;
if (k > 0) {
for (i = k - 1; !finished && !changed; i--) {
if (ar[i] < (n - 1) - (k - 1) + i) {
/* Increment this element */
ar[i]++;
if (i < k - 1) {
/* Turn the elements after it into a linear sequence */
unsigned int j;
for (j = i + 1; j < k; j++) {
ar[j] = ar[j - 1] + 1;
}
}
changed = 1;
}
finished = i == 0;
}
if (!changed) {
/* Reset to first combination */
for (i = 0; i < k; i++) {
ar[i] = i;
}
}
}
return changed;
}
typedef void(*printfn)(const void *, FILE *);
void print_set(const unsigned int *ar, size_t len, const void **elements,
const char *brackets, printfn print, FILE *fptr)
{
unsigned int i;
fputc(brackets[0], fptr);
for (i = 0; i < len; i++) {
print(elements[ar[i]], fptr);
if (i < len - 1) {
fputs(", ", fptr);
}
}
fputc(brackets[1], fptr);
}
int main(void)
{
unsigned int numbers[] = { 0, 1, 2 };
char *elements[] = { "a", "b", "c", "d", "e" };
const unsigned int k = sizeof(numbers) / sizeof(unsigned int);
const unsigned int n = sizeof(elements) / sizeof(const char*);
do {
print_set(numbers, k, (void*)elements, "[]", (printfn)fputs, stdout);
putchar('\n');
} while (next_combination(numbers, n, k));
getchar();
return 0;
}
Here is my Scala solution:
def combinations[A](s: List[A], k: Int): List[List[A]] =
if (k > s.length) Nil
else if (k == 1) s.map(List(_))
else combinations(s.tail, k - 1).map(s.head :: _) ::: combinations(s.tail, k)
Short fast C implementation
#include <stdio.h>
void main(int argc, char *argv[]) {
const int n = 6; /* The size of the set; for {1, 2, 3, 4} it's 4 */
const int p = 4; /* The size of the subsets; for {1, 2}, {1, 3}, ... it's 2 */
int comb[40] = {0}; /* comb[i] is the index of the i-th element in the combination */
int i = 0;
for (int j = 0; j <= n; j++) comb[j] = 0;
while (i >= 0) {
if (comb[i] < n + i - p + 1) {
comb[i]++;
if (i == p - 1) { for (int j = 0; j < p; j++) printf("%d ", comb[j]); printf("\n"); }
else { comb[++i] = comb[i - 1]; }
} else i--; }
}
To see how fast it is, use this code and test it
#include <time.h>
#include <stdio.h>
void main(int argc, char *argv[]) {
const int n = 32; /* The size of the set; for {1, 2, 3, 4} it's 4 */
const int p = 16; /* The size of the subsets; for {1, 2}, {1, 3}, ... it's 2 */
int comb[40] = {0}; /* comb[i] is the index of the i-th element in the combination */
int c = 0; int i = 0;
for (int j = 0; j <= n; j++) comb[j] = 0;
while (i >= 0) {
if (comb[i] < n + i - p + 1) {
comb[i]++;
/* if (i == p - 1) { for (int j = 0; j < p; j++) printf("%d ", comb[j]); printf("\n"); } */
if (i == p - 1) c++;
else { comb[++i] = comb[i - 1]; }
} else i--; }
printf("%d!%d == %d combination(s) in %15.3f second(s)\n ", p, n, c, clock()/1000.0);
}
test with cmd.exe (windows):
Microsoft Windows XP [Version 5.1.2600]
(C) Copyright 1985-2001 Microsoft Corp.
c:\Program Files\lcc\projects>combination
16!32 == 601080390 combination(s) in 5.781 second(s)
c:\Program Files\lcc\projects>
Have a nice day.
And here's a Clojure version that uses the same algorithm I describe in my OCaml implementation answer:
(defn select
([items]
(select items 0 (inc (count items))))
([items n1 n2]
(reduce concat
(map #(select % items)
(range n1 (inc n2)))))
([n items]
(let [
lmul (fn [a list-of-lists-of-bs]
(map #(cons a %) list-of-lists-of-bs))
]
(if (= n (count items))
(list items)
(if (empty? items)
items
(concat
(select n (rest items))
(lmul (first items) (select (dec n) (rest items)))))))))
It provides three ways to call it:
(a) for exactly n selected items as the question demands:
user=> (count (select 3 "abcdefgh"))
56
(b) for between n1 and n2 selected items:
user=> (select '(1 2 3 4) 2 3)
((3 4) (2 4) (2 3) (1 4) (1 3) (1 2) (2 3 4) (1 3 4) (1 2 4) (1 2 3))
(c) for between 0 and the size of the collection selected items:
user=> (select '(1 2 3))
(() (3) (2) (1) (2 3) (1 3) (1 2) (1 2 3))
void combine(char a[], int N, int M, int m, int start, char result[]) {
if (0 == m) {
for (int i = M - 1; i >= 0; i--)
std::cout << result[i];
std::cout << std::endl;
return;
}
for (int i = start; i < (N - m + 1); i++) {
result[m - 1] = a[i];
combine(a, N, M, m-1, i+1, result);
}
}
void combine(char a[], int N, int M) {
char *result = new char[M];
combine(a, N, M, M, 0, result);
delete[] result;
}
In the first function, m denotes how many more you need to choose, and start denotes from which position in array you must start choosing.
Since programming language is not mentioned I am assuming that lists are OK too. So here's an OCaml version suitable for short lists (non tail-recursive). Given a list l of elements of any type and an integer n it will return a list of all possible lists containing n elements of l if we assume that the order of the elements in the outcome lists is ignored, i.e. list ['a';'b'] is the same as ['b';'a'] and will reported once. So size of resultant list will be ((List.length l) Choose n).
The intuition of the recursion is the following: you take the head of the list and then make two recursive calls:
to combine the recursive results, list-multiply (please bear the odd name) the head of the list with the results of RC1 and then append (@) the results of RC2. List-multiply is the following operation lmul:
a lmul [ l1 ; l2 ; l3] = [a::l1 ; a::l2 ; a::l3]
lmul is implemented in the code below as
List.map (fun x -> h::x)
Recursion is terminated when the size of the list equals the number of elements you want to choose, in which case you just return the list itself.
So here's a four-liner in OCaml that implements the above algorithm:
let rec choose l n = match l, (List.length l) with
| _, lsize when n==lsize -> [l]
| h::t, _ -> (List.map (fun x-> h::x) (choose t (n-1))) @ (choose t n)
| [], _ -> []
In VB.Net, this algorithm collects all combinations of n numbers from a set of numbers (PoolArray). e.g. all combinations of 5 picks from "8,10,20,33,41,44,47".
Sub CreateAllCombinationsOfPicksFromPool(ByVal PicksArray() As UInteger, ByVal PicksIndex As UInteger, ByVal PoolArray() As UInteger, ByVal PoolIndex As UInteger)
If PicksIndex < PicksArray.Length Then
For i As Integer = PoolIndex To PoolArray.Length - PicksArray.Length + PicksIndex
PicksArray(PicksIndex) = PoolArray(i)
CreateAllCombinationsOfPicksFromPool(PicksArray, PicksIndex + 1, PoolArray, i + 1)
Next
Else
' completed combination. build your collections using PicksArray.
End If
End Sub
Dim PoolArray() As UInteger = Array.ConvertAll("8,10,20,33,41,44,47".Split(","), Function(u) UInteger.Parse(u))
Dim nPicks as UInteger = 5
Dim Picks(nPicks - 1) As UInteger
CreateAllCombinationsOfPicksFromPool(Picks, 0, PoolArray, 0)
This is a recursive program that generates combinations for nCk.Elements in collection are assumed to be from 1 to n
#include<stdio.h>
#include<stdlib.h>
int nCk(int n,int loopno,int ini,int *a,int k)
{
static int count=0;
int i;
loopno--;
if(loopno<0)
{
a[k-1]=ini;
for(i=0;i<k;i++)
{
printf("%d,",a[i]);
}
printf("\n");
count++;
return 0;
}
for(i=ini;i<=n-loopno-1;i++)
{
a[k-1-loopno]=i+1;
nCk(n,loopno,i+1,a,k);
}
if(ini==0)
return count;
else
return 0;
}
void main()
{
int n,k,*a,count;
printf("Enter the value of n and k\n");
scanf("%d %d",&n,&k);
a=(int*)malloc(k*sizeof(int));
count=nCk(n,k,0,a,k);
printf("No of combinations=%d\n",count);
}
A Lisp macro generates the code for all values r (taken-at-a-time)
(defmacro txaat (some-list taken-at-a-time)
(let* ((vars (reverse (truncate-list '(a b c d e f g h i j) taken-at-a-time))))
`(
,@(loop for i below taken-at-a-time
for j in vars
with nested = nil
finally (return nested)
do
(setf
nested
`(loop for ,j from
,(if (< i (1- (length vars)))
`(1+ ,(nth (1+ i) vars))
0)
below (- (length ,some-list) ,i)
,@(if (equal i 0)
`(collect
(list
,@(loop for k from (1- taken-at-a-time) downto 0
append `((nth ,(nth k vars) ,some-list)))))
`(append ,nested))))))))
So,
CL-USER> (macroexpand-1 '(txaat '(a b c d) 1))
(LOOP FOR A FROM 0 TO (- (LENGTH '(A B C D)) 1)
COLLECT (LIST (NTH A '(A B C D))))
T
CL-USER> (macroexpand-1 '(txaat '(a b c d) 2))
(LOOP FOR A FROM 0 TO (- (LENGTH '(A B C D)) 2)
APPEND (LOOP FOR B FROM (1+ A) TO (- (LENGTH '(A B C D)) 1)
COLLECT (LIST (NTH A '(A B C D)) (NTH B '(A B C D)))))
T
CL-USER> (macroexpand-1 '(txaat '(a b c d) 3))
(LOOP FOR A FROM 0 TO (- (LENGTH '(A B C D)) 3)
APPEND (LOOP FOR B FROM (1+ A) TO (- (LENGTH '(A B C D)) 2)
APPEND (LOOP FOR C FROM (1+ B) TO (- (LENGTH '(A B C D)) 1)
COLLECT (LIST (NTH A '(A B C D))
(NTH B '(A B C D))
(NTH C '(A B C D))))))
T
CL-USER>
And,
CL-USER> (txaat '(a b c d) 1)
((A) (B) (C) (D))
CL-USER> (txaat '(a b c d) 2)
((A B) (A C) (A D) (B C) (B D) (C D))
CL-USER> (txaat '(a b c d) 3)
((A B C) (A B D) (A C D) (B C D))
CL-USER> (txaat '(a b c d) 4)
((A B C D))
CL-USER> (txaat '(a b c d) 5)
NIL
CL-USER> (txaat '(a b c d) 0)
NIL
CL-USER>
Here's some simple code that prints all the C(n,m) combinations. It works by initializing and moving a set of array indices that point to next valid combination. The indices are initialized to point to the lowest m indices (lexicographically the smallest combination). Then on, starting with the m-th index, we try to move the indices forward. if an index has reached its limit, we try the previous index (all the way down to index 1). If we can move an index forward, then we reset all greater indices.
m=(rand()%n)+1; // m will vary from 1 to n
for (i=0;i<n;i++) a[i]=i+1;
// we want to print all possible C(n,m) combinations of selecting m objects out of n
printf("Printing C(%d,%d) possible combinations ...\n", n,m);
// This is an adhoc algo that keeps m pointers to the next valid combination
for (i=0;i<m;i++) p[i]=i; // the p[.] contain indices to the a vector whose elements constitute next combination
done=false;
while (!done)
{
// print combination
for (i=0;i<m;i++) printf("%2d ", a[p[i]]);
printf("\n");
// update combination
// method: start with p[m-1]. try to increment it. if it is already at the end, then try moving p[m-2] ahead.
// if this is possible, then reset p[m-1] to 1 more than (the new) p[m-2].
// if p[m-2] can not also be moved, then try p[m-3]. move that ahead. then reset p[m-2] and p[m-1].
// repeat all the way down to p[0]. if p[0] can not also be moved, then we have generated all combinations.
j=m-1;
i=1;
move_found=false;
while ((j>=0) && !move_found)
{
if (p[j]<(n-i))
{
move_found=true;
p[j]++; // point p[j] to next index
for (k=j+1;k<m;k++)
{
p[k]=p[j]+(k-j);
}
}
else
{
j--;
i++;
}
}
if (!move_found) done=true;
}
You can use the Asif's algorithm to generate all the possible combinations. It's probably the easiest and most efficient one. You can check out the medium article here.
Let's take a look in the implementation in JavaScript.
function Combinations( arr, r ) {
// To avoid object referencing, cloning the array.
arr = arr && arr.slice() || [];
var len = arr.length;
if( !len || r > len || !r )
return [ [] ];
else if( r === len )
return [ arr ];
if( r === len ) return arr.reduce( ( x, v ) => {
x.push( [ v ] );
return x;
}, [] );
var head = arr.shift();
return Combinations( arr, r - 1 ).map( x => {
x.unshift( head );
return x;
} ).concat( Combinations( arr, r ) );
}
// Now do your stuff.
console.log( Combinations( [ 'a', 'b', 'c', 'd', 'e' ], 3 ) );
There was recently a PowerShell challenge on the IronScripter website that needed an n-choose-k solution. I posted a solution there, but here is a more generic version.
function Get-NChooseK
{
[CmdletBinding()]
Param
(
[String[]]
$ArrayN
, [Int]
$ChooseK
, [Switch]
$AllK
, [String]
$Prefix = ''
)
PROCESS
{
# Validate the inputs
$ArrayN = $ArrayN | Sort-Object -Unique
If ($ChooseK -gt $ArrayN.Length)
{
Write-Error "Can't choose $ChooseK items when only $($ArrayN.Length) are available." -ErrorAction Stop
}
# Control the output
$firstK = If ($AllK) { 1 } Else { $ChooseK }
# Get combinations
$firstK..$ChooseK | ForEach-Object {
$thisK = $_
$ArrayN[0..($ArrayN.Length-($thisK--))] | ForEach-Object {
If ($thisK -eq 0)
{
Write-Output ($Prefix+$_)
}
Else
{
Get-NChooseK -Array ($ArrayN[($ArrayN.IndexOf($_)+1)..($ArrayN.Length-1)]) -Choose $thisK -AllK:$false -Prefix ($Prefix+$_)
}
}
}
}
}
E.g.:
PS C:\>$ArrayN = 'E','B','C','A','D'
PS C:\>$ChooseK = 3
PS C:\>Get-NChooseK -ArrayN $ArrayN -ChooseK $ChooseK
ABC
ABD
ABE
ACD
ACE
ADE
BCD
BCE
BDE
CDE
Here is a simple und understandable recursive C++ solution:
#include<vector>
using namespace std;
template<typename T>
void ksubsets(const vector<T>& arr, unsigned left, unsigned idx,
vector<T>& lst, vector<vector<T>>& res)
{
if (left < 1) {
res.push_back(lst);
return;
}
for (unsigned i = idx; i < arr.size(); i++) {
lst.push_back(arr[i]);
ksubsets(arr, left - 1, i + 1, lst, res);
lst.pop_back();
}
}
int main()
{
vector<int> arr = { 1, 2, 3, 4, 5 };
unsigned left = 3;
vector<int> lst;
vector<vector<int>> res;
ksubsets<int>(arr, left, 0, lst, res);
// now res has all the combinations
}
Below is an iterative algorithm in C++ that does not use the STL nor recursion nor conditional nested loops. It is faster that way, it does not perform any element swaps and it does not burden the stack with recursion and it can also be easily ported to ANSI C by substituting mallloc(), free() and printf() for new, delete and std::cout, respectively.
If you want to display the elements with a different or longer alphabet then change the *alphabet parameter to point to a different string than "abcdefg".
void OutputArrayChar(unsigned int* ka, size_t n, const char *alphabet) {
for (int i = 0; i < n; i++)
std::cout << alphabet[ka[i]] << ",";
std::cout << endl;
}
void GenCombinations(const unsigned int N, const unsigned int K, const char *alphabet) {
unsigned int *ka = new unsigned int [K]; //dynamically allocate an array of UINTs
unsigned int ki = K-1; //Point ki to the last elemet of the array
ka[ki] = N-1; //Prime the last elemet of the array.
while (true) {
unsigned int tmp = ka[ki]; //Optimization to prevent reading ka[ki] repeatedly
while (ki) //Fill to the left with consecutive descending values (blue squares)
ka[--ki] = --tmp;
OutputArrayChar(ka, K, alphabet);
while (--ka[ki] == ki) { //Decrement and check if the resulting value equals the index (bright green squares)
OutputArrayChar(ka, K, alphabet);
if (++ki == K) { //Exit condition (all of the values in the array are flush to the left)
delete[] ka;
return;
}
}
}
}
int main(int argc, char *argv[])
{
GenCombinations(7, 4, "abcdefg");
return 0;
}
IMPORTANT: The *alphabet parameter must point to a string with at least N characters. You can also pass an address of a string which is defined somewhere else.
Combinations: Out of "7 Choose 4".
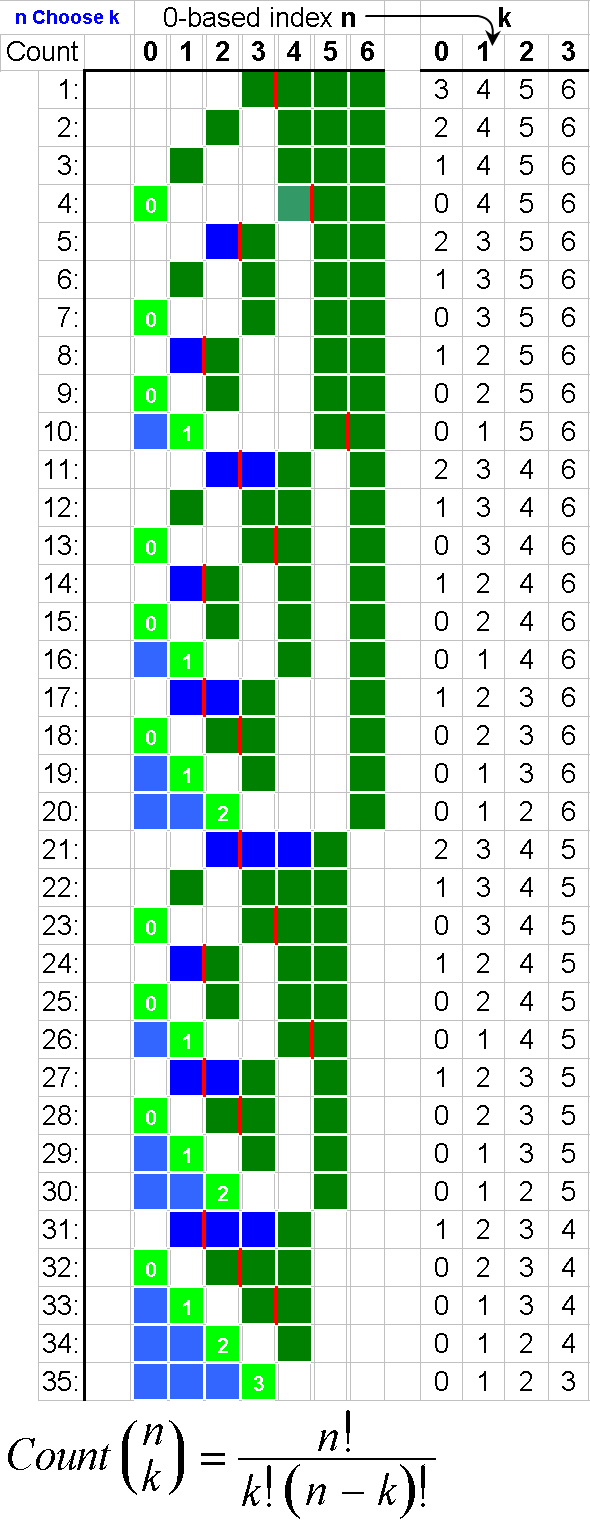
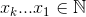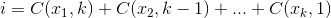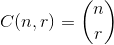I'm aware that there are a LOT of answers to this already, but I thought I'd add my own individual contribution in JavaScript, which consists of two functions - one to generate all the possible distinct k-subsets of an original n-element set, and one to use that first function to generate the power set of the original n-element set.
Here is the code for the two functions:
//Generate combination subsets from a base set of elements (passed as an array). This function should generate an
//array containing nCr elements, where nCr = n!/[r! (n-r)!].
//Arguments:
//[1] baseSet : The base set to create the subsets from (e.g., ["a", "b", "c", "d", "e", "f"])
//[2] cnt : The number of elements each subset is to contain (e.g., 3)
function MakeCombinationSubsets(baseSet, cnt)
{
var bLen = baseSet.length;
var indices = [];
var subSet = [];
var done = false;
var result = []; //Contains all the combination subsets generated
var done = false;
var i = 0;
var idx = 0;
var tmpIdx = 0;
var incr = 0;
var test = 0;
var newIndex = 0;
var inBounds = false;
var tmpIndices = [];
var checkBounds = false;
//First, generate an array whose elements are indices into the base set ...
for (i=0; i<cnt; i++)
indices.push(i);
//Now create a clone of this array, to be used in the loop itself ...
tmpIndices = [];
tmpIndices = tmpIndices.concat(indices);
//Now initialise the loop ...
idx = cnt - 1; //point to the last element of the indices array
incr = 0;
done = false;
while (!done)
{
//Create the current subset ...
subSet = []; //Make sure we begin with a completely empty subset before continuing ...
for (i=0; i<cnt; i++)
subSet.push(baseSet[tmpIndices[i]]); //Create the current subset, using items selected from the
//base set, using the indices array (which will change as we
//continue scanning) ...
//Add the subset thus created to the result set ...
result.push(subSet);
//Now update the indices used to select the elements of the subset. At the start, idx will point to the
//rightmost index in the indices array, but the moment that index moves out of bounds with respect to the
//base set, attention will be shifted to the next left index.
test = tmpIndices[idx] + 1;
if (test >= bLen)
{
//Here, we're about to move out of bounds with respect to the base set. We therefore need to scan back,
//and update indices to the left of the current one. Find the leftmost index in the indices array that
//isn't going to move out of bounds with respect to the base set ...
tmpIdx = idx - 1;
incr = 1;
inBounds = false; //Assume at start that the index we're checking in the loop below is out of bounds
checkBounds = true;
while (checkBounds)
{
if (tmpIdx < 0)
{
checkBounds = false; //Exit immediately at this point
}
else
{
newIndex = tmpIndices[tmpIdx] + 1;
test = newIndex + incr;
if (test >= bLen)
{
//Here, incrementing the current selected index will take that index out of bounds, so
//we move on to the next index to the left ...
tmpIdx--;
incr++;
}
else
{
//Here, the index will remain in bounds if we increment it, so we
//exit the loop and signal that we're in bounds ...
inBounds = true;
checkBounds = false;
//End if/else
}
//End if
}
//End while
}
//At this point, if we'er still in bounds, then we continue generating subsets, but if not, we abort immediately.
if (!inBounds)
done = true;
else
{
//Here, we're still in bounds. We need to update the indices accordingly. NOTE: at this point, although a
//left positioned index in the indices array may still be in bounds, incrementing it to generate indices to
//the right may take those indices out of bounds. We therefore need to check this as we perform the index
//updating of the indices array.
tmpIndices[tmpIdx] = newIndex;
inBounds = true;
checking = true;
i = tmpIdx + 1;
while (checking)
{
test = tmpIndices[i - 1] + 1; //Find out if incrementing the left adjacent index takes it out of bounds
if (test >= bLen)
{
inBounds = false; //If we move out of bounds, exit NOW ...
checking = false;
}
else
{
tmpIndices[i] = test; //Otherwise, update the indices array ...
i++; //Now move on to the next index to the right in the indices array ...
checking = (i < cnt); //And continue until we've exhausted all the indices array elements ...
//End if/else
}
//End while
}
//At this point, if the above updating of the indices array has moved any of its elements out of bounds,
//we abort subset construction from this point ...
if (!inBounds)
done = true;
//End if/else
}
}
else
{
//Here, the rightmost index under consideration isn't moving out of bounds with respect to the base set when
//we increment it, so we simply increment and continue the loop ...
tmpIndices[idx] = test;
//End if
}
//End while
}
return(result);
//End function
}
function MakePowerSet(baseSet)
{
var bLen = baseSet.length;
var result = [];
var i = 0;
var partialSet = [];
result.push([]); //add the empty set to the power set
for (i=1; i<bLen; i++)
{
partialSet = MakeCombinationSubsets(baseSet, i);
result = result.concat(partialSet);
//End i loop
}
//Now, finally, add the base set itself to the power set to make it complete ...
partialSet = [];
partialSet.push(baseSet);
result = result.concat(partialSet);
return(result);
//End function
}
I tested this with the set ["a", "b", "c", "d", "e", "f"] as the base set, and ran the code to produce the following power set:
[]
["a"]
["b"]
["c"]
["d"]
["e"]
["f"]
["a","b"]
["a","c"]
["a","d"]
["a","e"]
["a","f"]
["b","c"]
["b","d"]
["b","e"]
["b","f"]
["c","d"]
["c","e"]
["c","f"]
["d","e"]
["d","f"]
["e","f"]
["a","b","c"]
["a","b","d"]
["a","b","e"]
["a","b","f"]
["a","c","d"]
["a","c","e"]
["a","c","f"]
["a","d","e"]
["a","d","f"]
["a","e","f"]
["b","c","d"]
["b","c","e"]
["b","c","f"]
["b","d","e"]
["b","d","f"]
["b","e","f"]
["c","d","e"]
["c","d","f"]
["c","e","f"]
["d","e","f"]
["a","b","c","d"]
["a","b","c","e"]
["a","b","c","f"]
["a","b","d","e"]
["a","b","d","f"]
["a","b","e","f"]
["a","c","d","e"]
["a","c","d","f"]
["a","c","e","f"]
["a","d","e","f"]
["b","c","d","e"]
["b","c","d","f"]
["b","c","e","f"]
["b","d","e","f"]
["c","d","e","f"]
["a","b","c","d","e"]
["a","b","c","d","f"]
["a","b","c","e","f"]
["a","b","d","e","f"]
["a","c","d","e","f"]
["b","c","d","e","f"]
["a","b","c","d","e","f"]
Just copy and paste those two functions "as is", and you'll have the basics needed to extract the distinct k-subsets of an n-element set, and generate the power set of that n-element set if you wish.
I don't claim this to be elegant, merely that it works after a lot of testing (and turning the air blue during the debugging phase :) ).
Here is a simple JS solution:
function getAllCombinations(n, k, f1) {
indexes = Array(k);
for (let i =0; i< k; i++) {
indexes[i] = i;
}
var total = 1;
f1(indexes);
while (indexes[0] !== n-k) {
total++;
getNext(n, indexes);
f1(indexes);
}
return {total};
}
function getNext(n, vec) {
const k = vec.length;
vec[k-1]++;
for (var i=0; i<k; i++) {
var currentIndex = k-i-1;
if (vec[currentIndex] === n - i) {
var nextIndex = k-i-2;
vec[nextIndex]++;
vec[currentIndex] = vec[nextIndex] + 1;
}
}
for (var i=1; i<k; i++) {
if (vec[i] === n - (k-i - 1)) {
vec[i] = vec[i-1] + 1;
}
}
return vec;
}
let start = new Date();
let result = getAllCombinations(10, 3, indexes => console.log(indexes));
let runTime = new Date() - start;
console.log({
result, runTime
});Very fast combinations for MetaTrader MQL4 implemented as iterator object.
The code is so simple to understand.
I benchmarked a lot of algorithms, this one is really very fast - about 3x faster than most next_combination() functions.
class CombinationsIterator
{
private:
int input_array[]; // 1 2 3 4 5
int index_array[]; // i j k
int m_elements; // N
int m_indices; // K
public:
CombinationsIterator(int &src_data[], int k)
{
m_indices = k;
m_elements = ArraySize(src_data);
ArrayCopy(input_array, src_data);
ArrayResize(index_array, m_indices);
// create initial combination (0..k-1)
for (int i = 0; i < m_indices; i++)
{
index_array[i] = i;
}
}
// https://stackoverflow.com/questions/5076695
// bool next_combination(int &item[], int k, int N)
bool advance()
{
int N = m_elements;
for (int i = m_indices - 1; i >= 0; --i)
{
if (index_array[i] < --N)
{
++index_array[i];
for (int j = i + 1; j < m_indices; ++j)
{
index_array[j] = index_array[j - 1] + 1;
}
return true;
}
}
return false;
}
void getItems(int &items[])
{
// fill items[] from input array
for (int i = 0; i < m_indices; i++)
{
items[i] = input_array[index_array[i]];
}
}
};A driver program to test the above iterator class:
//+------------------------------------------------------------------+
//| |
//+------------------------------------------------------------------+
// driver program to test above class
#define N 5
#define K 3
void OnStart()
{
int myset[N] = {1, 2, 3, 4, 5};
int items[K];
CombinationsIterator comboIt(myset, K);
do
{
comboIt.getItems(items);
printf("%s", ArrayToString(items));
} while (comboIt.advance());
}Output:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5I made a general class for combinations in C++. It is used like this.
char ar[] = "0ABCDEFGH";
nCr ncr(8, 3);
while(ncr.next()) {
for(int i=0; i<ncr.size(); i++) cout << ar[ncr[i]];
cout << ' ';
}
My library ncr[i] returns from 1, not from 0. That's why there is 0 in the array. If you want to consider order, just chage nCr class to nPr. Usage is identical.
Result
ABC ABD ABE ABF ABG ABH ACD ACE ACF ACG ACH ADE ADF ADG ADH AEF AEG AEH AFG AFH AGH BCD BCE BCF BCG BCH BDE BDF BDG BDH BEF BEG BEH BFG BFH BGH CDE CDF CDG CDH CEF CEG CEH CFG CFH CGH DEF DEG DEH DFG DFH DGH EFG EFH EGH FGH
Here goes the header file.
#pragma once
#include <exception>
class NRexception : public std::exception
{
public:
virtual const char* what() const throw() {
return "Combination : N, R should be positive integer!!";
}
};
class Combination
{
public:
Combination(int n, int r);
virtual ~Combination() { delete [] ar;}
int& operator[](unsigned i) {return ar[i];}
bool next();
int size() {return r;}
static int factorial(int n);
protected:
int* ar;
int n, r;
};
class nCr : public Combination
{
public:
nCr(int n, int r);
bool next();
int count() const;
};
class nTr : public Combination
{
public:
nTr(int n, int r);
bool next();
int count() const;
};
class nHr : public nTr
{
public:
nHr(int n, int r) : nTr(n,r) {}
bool next();
int count() const;
};
class nPr : public Combination
{
public:
nPr(int n, int r);
virtual ~nPr() {delete [] on;}
bool next();
void rewind();
int count() const;
private:
bool* on;
void inc_ar(int i);
};
And the implementation.
#include "combi.h"
#include <set>
#include<cmath>
Combination::Combination(int n, int r)
{
//if(n < 1 || r < 1) throw NRexception();
ar = new int[r];
this->n = n;
this->r = r;
}
int Combination::factorial(int n)
{
return n == 1 ? n : n * factorial(n-1);
}
int nPr::count() const
{
return factorial(n)/factorial(n-r);
}
int nCr::count() const
{
return factorial(n)/factorial(n-r)/factorial(r);
}
int nTr::count() const
{
return pow(n, r);
}
int nHr::count() const
{
return factorial(n+r-1)/factorial(n-1)/factorial(r);
}
nCr::nCr(int n, int r) : Combination(n, r)
{
if(r == 0) return;
for(int i=0; i<r-1; i++) ar[i] = i + 1;
ar[r-1] = r-1;
}
nTr::nTr(int n, int r) : Combination(n, r)
{
for(int i=0; i<r-1; i++) ar[i] = 1;
ar[r-1] = 0;
}
bool nCr::next()
{
if(r == 0) return false;
ar[r-1]++;
int i = r-1;
while(ar[i] == n-r+2+i) {
if(--i == -1) return false;
ar[i]++;
}
while(i < r-1) ar[i+1] = ar[i++] + 1;
return true;
}
bool nTr::next()
{
ar[r-1]++;
int i = r-1;
while(ar[i] == n+1) {
ar[i] = 1;
if(--i == -1) return false;
ar[i]++;
}
return true;
}
bool nHr::next()
{
ar[r-1]++;
int i = r-1;
while(ar[i] == n+1) {
if(--i == -1) return false;
ar[i]++;
}
while(i < r-1) ar[i+1] = ar[i++];
return true;
}
nPr::nPr(int n, int r) : Combination(n, r)
{
on = new bool[n+2];
for(int i=0; i<n+2; i++) on[i] = false;
for(int i=0; i<r; i++) {
ar[i] = i + 1;
on[i] = true;
}
ar[r-1] = 0;
}
void nPr::rewind()
{
for(int i=0; i<r; i++) {
ar[i] = i + 1;
on[i] = true;
}
ar[r-1] = 0;
}
bool nPr::next()
{
inc_ar(r-1);
int i = r-1;
while(ar[i] == n+1) {
if(--i == -1) return false;
inc_ar(i);
}
while(i < r-1) {
ar[++i] = 0;
inc_ar(i);
}
return true;
}
void nPr::inc_ar(int i)
{
on[ar[i]] = false;
while(on[++ar[i]]);
if(ar[i] != n+1) on[ar[i]] = true;
}
Simple but slow C++ backtracking algorithm.
#include <iostream>
void backtrack(int* numbers, int n, int k, int i, int s)
{
if (i == k)
{
for (int j = 0; j < k; ++j)
{
std::cout << numbers[j];
}
std::cout << std::endl;
return;
}
if (s > n)
{
return;
}
numbers[i] = s;
backtrack(numbers, n, k, i + 1, s + 1);
backtrack(numbers, n, k, i, s + 1);
}
int main(int argc, char* argv[])
{
int n = 5;
int k = 3;
int* numbers = new int[k];
backtrack(numbers, n, k, 0, 1);
delete[] numbers;
return 0;
}
There is no need for collection manipulations. The problem is almost the same as cycling over K nested loops but you have to be careful with the indexes and bounds (ignoring Java and OOP stuff):
public class CombinationsGen {
private final int n;
private final int k;
private int[] buf;
public CombinationsGen(int n, int k) {
this.n = n;
this.k = k;
}
public void combine(Consumer<int[]> consumer) {
buf = new int[k];
rec(0, 0, consumer);
}
private void rec(int index, int next, Consumer<int[]> consumer) {
int max = n - index;
if (index == k - 1) {
for (int i = 0; i < max && next < n; i++) {
buf[index] = next;
next++;
consumer.accept(buf);
}
} else {
for (int i = 0; i < max && next + index < n; i++) {
buf[index] = next;
next++;
rec(index + 1, next, consumer);
}
}
}
}
Use like so:
CombinationsGen gen = new CombinationsGen(5, 2);
AtomicInteger total = new AtomicInteger();
gen.combine(arr -> {
System.out.println(Arrays.toString(arr));
total.incrementAndGet();
});
System.out.println(total);
Get expected results:
[0, 1]
[0, 2]
[0, 3]
[0, 4]
[1, 2]
[1, 3]
[1, 4]
[2, 3]
[2, 4]
[3, 4]
10
Finally, map the indexes to whatever set of data you may have.
Recursively, a very simple answer, combo, in Free Pascal.
procedure combinata (n, k :integer; producer :oneintproc);
procedure combo (ndx, nbr, len, lnd :integer);
begin
for nbr := nbr to len do begin
productarray[ndx] := nbr;
if len < lnd then
combo(ndx+1,nbr+1,len+1,lnd)
else
producer(k);
end;
end;
begin
combo (0, 0, n-k, n-1);
end;
"producer" disposes of the productarray made for each combination.
Here is an algorithm i came up with for solving this problem. Its written in c++, but can be adapted to pretty much any language that supports bitwise operations.
void r_nCr(const unsigned int &startNum, const unsigned int &bitVal, const unsigned int &testNum) // Should be called with arguments (2^r)-1, 2^(r-1), 2^(n-1)
{
unsigned int n = (startNum - bitVal) << 1;
n += bitVal ? 1 : 0;
for (unsigned int i = log2(testNum) + 1; i > 0; i--) // Prints combination as a series of 1s and 0s
cout << (n >> (i - 1) & 1);
cout << endl;
if (!(n & testNum) && n != startNum)
r_nCr(n, bitVal, testNum);
if (bitVal && bitVal < testNum)
r_nCr(startNum, bitVal >> 1, testNum);
}
You can see an explanation of how it works here.
C# simple algorithm. (I'm posting it since I've tried to use the one you guys uploaded, but for some reason I couldn't compile it - extending a class? so I wrote my own one just in case someone else is facing the same problem I did). I'm not much into c# more than basic programming by the way, but this one works fine.
public static List<List<int>> GetSubsetsOfSizeK(List<int> lInputSet, int k)
{
List<List<int>> lSubsets = new List<List<int>>();
GetSubsetsOfSizeK_rec(lInputSet, k, 0, new List<int>(), lSubsets);
return lSubsets;
}
public static void GetSubsetsOfSizeK_rec(List<int> lInputSet, int k, int i, List<int> lCurrSet, List<List<int>> lSubsets)
{
if (lCurrSet.Count == k)
{
lSubsets.Add(lCurrSet);
return;
}
if (i >= lInputSet.Count)
return;
List<int> lWith = new List<int>(lCurrSet);
List<int> lWithout = new List<int>(lCurrSet);
lWith.Add(lInputSet[i++]);
GetSubsetsOfSizeK_rec(lInputSet, k, i, lWith, lSubsets);
GetSubsetsOfSizeK_rec(lInputSet, k, i, lWithout, lSubsets);
}
USAGE: GetSubsetsOfSizeK(set of type List<int>, integer k)
You can modify it to iterate over whatever you are working with.
Good luck!
Here's a C++ solution i came up with using recursion and bit-shifting. It may work in C as well.
void r_nCr(unsigned int startNum, unsigned int bitVal, unsigned int testNum) // Should be called with arguments (2^r)-1, 2^(r-1), 2^(n-1)
{
unsigned int n = (startNum - bitVal) << 1;
n += bitVal ? 1 : 0;
for (unsigned int i = log2(testNum) + 1; i > 0; i--) // Prints combination as a series of 1s and 0s
cout << (n >> (i - 1) & 1);
cout << endl;
if (!(n & testNum) && n != startNum)
r_nCr(n, bitVal, testNum);
if (bitVal && bitVal < testNum)
r_nCr(startNum, bitVal >> 1, testNum);
}
You can find an explanation of how this works here.
Short fast C# implementation
public static IEnumerable<IEnumerable<T>> Combinations<T>(IEnumerable<T> elements, int k)
{
return Combinations(elements.Count(), k).Select(p => p.Select(q => elements.ElementAt(q)));
}
public static List<int[]> Combinations(int setLenght, int subSetLenght) //5, 3
{
var result = new List<int[]>();
var lastIndex = subSetLenght - 1;
var dif = setLenght - subSetLenght;
var prevSubSet = new int[subSetLenght];
var lastSubSet = new int[subSetLenght];
for (int i = 0; i < subSetLenght; i++)
{
prevSubSet[i] = i;
lastSubSet[i] = i + dif;
}
while(true)
{
//add subSet ad result set
var n = new int[subSetLenght];
for (int i = 0; i < subSetLenght; i++)
n[i] = prevSubSet[i];
result.Add(n);
if (prevSubSet[0] >= lastSubSet[0])
break;
//start at index 1 because index 0 is checked and breaking in the current loop
int j = 1;
for (; j < subSetLenght; j++)
{
if (prevSubSet[j] >= lastSubSet[j])
{
prevSubSet[j - 1]++;
for (int p = j; p < subSetLenght; p++)
prevSubSet[p] = prevSubSet[p - 1] + 1;
break;
}
}
if (j > lastIndex)
prevSubSet[lastIndex]++;
}
return result;
}
Perhaps I've missed the point (that you need the algorithm and not the ready made solution), but it seems that scala does it out of the box (now):
def combis(str:String, k:Int):Array[String] = {
str.combinations(k).toArray
}
Using the method like this:
println(combis("abcd",2).toList)
Will produce:
List(ab, ac, ad, bc, bd, cd)
Here's a coffeescript implementation
combinations: (list, n) ->
permuations = Math.pow(2, list.length) - 1
out = []
combinations = []
while permuations
out = []
for i in [0..list.length]
y = ( 1 << i )
if( y & permuations and (y isnt permuations))
out.push(list[i])
if out.length <= n and out.length > 0
combinations.push(out)
permuations--
return combinations
yet another recursive solution (you should be able to port this to use letters instead of numbers) using a stack, a bit shorter than most though:
stack = []
def choose(n,x):
r(0,0,n+1,x)
def r(p, c, n,x):
if x-c == 0:
print stack
return
for i in range(p, n-(x-1)+c):
stack.append(i)
r(i+1,c+1,n,x)
stack.pop()
4 choose 3 or I want all 3 combinations of numbers starting with 0 to 4
choose(4,3)
[0, 1, 2]
[0, 1, 3]
[0, 1, 4]
[0, 2, 3]
[0, 2, 4]
[0, 3, 4]
[1, 2, 3]
[1, 2, 4]
[1, 3, 4]
[2, 3, 4]
How about this answer ...this prints all combinations of length 3 ...and it can generalised for any length ... Working code ...
#include<iostream>
#include<string>
using namespace std;
void combination(string a,string dest){
int l = dest.length();
if(a.empty() && l == 3 ){
cout<<dest<<endl;}
else{
if(!a.empty() && dest.length() < 3 ){
combination(a.substr(1,a.length()),dest+a[0]);}
if(!a.empty() && dest.length() <= 3 ){
combination(a.substr(1,a.length()),dest);}
}
}
int main(){
string demo("abcd");
combination(demo,"");
return 0;
}
This is my contribution in javascript (no recursion)
set = ["q0", "q1", "q2", "q3"]
collector = []
function comb(num) {
results = []
one_comb = []
for (i = set.length - 1; i >= 0; --i) {
tmp = Math.pow(2, i)
quotient = parseInt(num / tmp)
results.push(quotient)
num = num % tmp
}
k = 0
for (i = 0; i < results.length; ++i)
if (results[i]) {
++k
one_comb.push(set[i])
}
if (collector[k] == undefined)
collector[k] = []
collector[k].push(one_comb)
}
sum = 0
for (i = 0; i < set.length; ++i)
sum += Math.pow(2, i)
for (ii = sum; ii > 0; --ii)
comb(ii)
cnt = 0
for (i = 1; i < collector.length; ++i) {
n = 0
for (j = 0; j < collector[i].length; ++j)
document.write(++cnt, " - " + (++n) + " - ", collector[i][j], "<br>")
document.write("<hr>")
}
In Python, taking advantage of recursion and the fact that everything is done by reference. This will take a lot of memory for very large sets, but has the advantage that the initial set can be a complex object. It will find only unique combinations.
import copy
def find_combinations( length, set, combinations = None, candidate = None ):
# recursive function to calculate all unique combinations of unique values
# from [set], given combinations of [length]. The result is populated
# into the 'combinations' list.
#
if combinations == None:
combinations = []
if candidate == None:
candidate = []
for item in set:
if item in candidate:
# this item already appears in the current combination somewhere.
# skip it
continue
attempt = copy.deepcopy(candidate)
attempt.append(item)
# sorting the subset is what gives us completely unique combinations,
# so that [1, 2, 3] and [1, 3, 2] will be treated as equals
attempt.sort()
if len(attempt) < length:
# the current attempt at finding a new combination is still too
# short, so add another item to the end of the set
# yay recursion!
find_combinations( length, set, combinations, attempt )
else:
# the current combination attempt is the right length. If it
# already appears in the list of found combinations then we'll
# skip it.
if attempt in combinations:
continue
else:
# otherwise, we append it to the list of found combinations
# and move on.
combinations.append(attempt)
continue
return len(combinations)
You use it this way. Passing 'result' is optional, so you could just use it to get the number of possible combinations... although that would be really inefficient (it's better done by calculation).
size = 3
set = [1, 2, 3, 4, 5]
result = []
num = find_combinations( size, set, result )
print "size %d results in %d sets" % (size, num)
print "result: %s" % (result,)
You should get the following output from that test data:
size 3 results in 10 sets
result: [[1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]
And it will work just as well if your set looks like this:
set = [
[ 'vanilla', 'cupcake' ],
[ 'chocolate', 'pudding' ],
[ 'vanilla', 'pudding' ],
[ 'chocolate', 'cookie' ],
[ 'mint', 'cookie' ]
]
In Python like Andrea Ambu, but not hardcoded for choosing three.
def combinations(list, k):
"""Choose combinations of list, choosing k elements(no repeats)"""
if len(list) < k:
return []
else:
seq = [i for i in range(k)]
while seq:
print [list[index] for index in seq]
seq = get_next_combination(len(list), k, seq)
def get_next_combination(num_elements, k, seq):
index_to_move = find_index_to_move(num_elements, seq)
if index_to_move == None:
return None
else:
seq[index_to_move] += 1
#for every element past this sequence, move it down
for i, elem in enumerate(seq[(index_to_move+1):]):
seq[i + 1 + index_to_move] = seq[index_to_move] + i + 1
return seq
def find_index_to_move(num_elements, seq):
"""Tells which index should be moved"""
for rev_index, elem in enumerate(reversed(seq)):
if elem < (num_elements - rev_index - 1):
return len(seq) - rev_index - 1
return None
A PowerShell solution:
function Get-NChooseK
{
<#
.SYNOPSIS
Returns all the possible combinations by choosing K items at a time from N possible items.
.DESCRIPTION
Returns all the possible combinations by choosing K items at a time from N possible items.
The combinations returned do not consider the order of items as important i.e. 123 is considered to be the same combination as 231, etc.
.PARAMETER ArrayN
The array of items to choose from.
.PARAMETER ChooseK
The number of items to choose.
.PARAMETER AllK
Includes combinations for all lesser values of K above zero i.e. 1 to K.
.PARAMETER Prefix
String that will prefix each line of the output.
.EXAMPLE
PS C:\> Get-NChooseK -ArrayN '1','2','3' -ChooseK 3
123
.EXAMPLE
PS C:\> Get-NChooseK -ArrayN '1','2','3' -ChooseK 3 -AllK
1
2
3
12
13
23
123
.EXAMPLE
PS C:\> Get-NChooseK -ArrayN '1','2','3' -ChooseK 2 -Prefix 'Combo: '
Combo: 12
Combo: 13
Combo: 23
.NOTES
Author : nmbell
#>
# Use cmdlet binding
[CmdletBinding()]
# Declare parameters
Param
(
[String[]]
$ArrayN
, [Int]
$ChooseK
, [Switch]
$AllK
, [String]
$Prefix = ''
)
BEGIN
{
}
PROCESS
{
# Validate the inputs
$ArrayN = $ArrayN | Sort-Object -Unique
If ($ChooseK -gt $ArrayN.Length)
{
Write-Error "Can't choose $ChooseK items when only $($ArrayN.Length) are available." -ErrorAction Stop
}
# Control the output
$firstK = If ($AllK) { 1 } Else { $ChooseK }
# Get combinations
$firstK..$ChooseK | ForEach-Object {
$thisK = $_
$ArrayN[0..($ArrayN.Length-($thisK--))] | ForEach-Object {
If ($thisK -eq 0)
{
Write-Output ($Prefix+$_)
}
Else
{
Get-NChooseK -Array ($ArrayN[($ArrayN.IndexOf($_)+1)..($ArrayN.Length-1)]) -Choose $thisK -AllK:$false -Prefix ($Prefix+$_)
}
}
}
}
END
{
}
}
E.g.:
PS C:\>Get-NChooseK -ArrayN 'A','B','C','D','E' -ChooseK 3
ABC
ABD
ABE
ACD
ACE
ADE
BCD
BCE
BDE
CDE
There was a challenge posted recently on the IronScripter website similar to this question, where you can find links to mine and some other solutions.
I'd like to present my solution. No recursive calls, nor nested loops in next.
The core of code is next() method.
public class Combinations {
final int pos[];
final List<Object> set;
public Combinations(List<?> l, int k) {
pos = new int[k];
set=new ArrayList<Object>(l);
reset();
}
public void reset() {
for (int i=0; i < pos.length; ++i) pos[i]=i;
}
public boolean next() {
int i = pos.length-1;
for (int maxpos = set.size()-1; pos[i] >= maxpos; --maxpos) {
if (i==0) return false;
--i;
}
++pos[i];
while (++i < pos.length)
pos[i]=pos[i-1]+1;
return true;
}
public void getSelection(List<?> l) {
@SuppressWarnings("unchecked")
List<Object> ll = (List<Object>)l;
if (ll.size()!=pos.length) {
ll.clear();
for (int i=0; i < pos.length; ++i)
ll.add(set.get(pos[i]));
}
else {
for (int i=0; i < pos.length; ++i)
ll.set(i, set.get(pos[i]));
}
}
}
And usage example:
static void main(String[] args) {
List<Character> l = new ArrayList<Character>();
for (int i=0; i < 32; ++i) l.add((char)('a'+i));
Combinations comb = new Combinations(l,5);
int n=0;
do {
++n;
comb.getSelection(l);
//Log.debug("%d: %s", n, l.toString());
} while (comb.next());
Log.debug("num = %d", n);
}
#include <unistd.h>
#include <stdio.h>
#include <iconv.h>
#include <string.h>
#include <errno.h>
#include <stdlib.h>
int main(int argc, char **argv)
{
int opt = -1, min_len = 0, max_len = 0;
char ofile[256], fchar[2], tchar[2];
ofile[0] = 0;
fchar[0] = 0;
tchar[0] = 0;
while((opt = getopt(argc, argv, "o:f:t:l:L:")) != -1)
{
switch(opt)
{
case 'o':
strncpy(ofile, optarg, 255);
break;
case 'f':
strncpy(fchar, optarg, 1);
break;
case 't':
strncpy(tchar, optarg, 1);
break;
case 'l':
min_len = atoi(optarg);
break;
case 'L':
max_len = atoi(optarg);
break;
default:
printf("usage: %s -oftlL\n\t-o output file\n\t-f from char\n\t-t to char\n\t-l min seq len\n\t-L max seq len", argv[0]);
}
}
if(max_len < 1)
{
printf("error, length must be more than 0\n");
return 1;
}
if(min_len > max_len)
{
printf("error, max length must be greater or equal min_length\n");
return 1;
}
if((int)fchar[0] > (int)tchar[0])
{
printf("error, invalid range specified\n");
return 1;
}
FILE *out = fopen(ofile, "w");
if(!out)
{
printf("failed to open input file with error: %s\n", strerror(errno));
return 1;
}
int cur_len = min_len;
while(cur_len <= max_len)
{
char buf[cur_len];
for(int i = 0; i < cur_len; i++)
buf[i] = fchar[0];
fwrite(buf, cur_len, 1, out);
fwrite("\n", 1, 1, out);
while(buf[0] != (tchar[0]+1))
{
while(buf[cur_len-1] < tchar[0])
{
(int)buf[cur_len-1]++;
fwrite(buf, cur_len, 1, out);
fwrite("\n", 1, 1, out);
}
if(cur_len < 2)
break;
if(buf[0] == tchar[0])
{
bool stop = true;
for(int i = 1; i < cur_len; i++)
{
if(buf[i] != tchar[0])
{
stop = false;
break;
}
}
if(stop)
break;
}
int u = cur_len-2;
for(; u>=0 && buf[u] >= tchar[0]; u--)
;
(int)buf[u]++;
for(int i = u+1; i < cur_len; i++)
buf[i] = fchar[0];
fwrite(buf, cur_len, 1, out);
fwrite("\n", 1, 1, out);
}
cur_len++;
}
fclose(out);
return 0;
}
here my implementation in c++, it write all combinations to specified files, but behaviour can be changed, i made in to generate various dictionaries, it accept min and max length and character range, currently only ansi supported, it enough for my needs
© 2022 - 2024 — McMap. All rights reserved.