Why does scipy.norm.pdf sometimes give PDF > 1? How to correct it?

Question

Given mean and variance of a Gaussian (normal) random variable, I would like to compute its probability density function (PDF).

I referred this post: Calculate probability in normal distribution given mean, std in Python,

Also the scipy docs: scipy.stats.norm

But when I plot a PDF of a curve, the probability exceeds 1! Refer to this minimum working example:

import numpy as np
import scipy.stats as stats

x = np.linspace(0.3, 1.75, 1000)
plt.plot(x, stats.norm.pdf(x, 1.075, 0.2))
plt.show()

This is what I get:

How is it even possible to have 200% probability to get the mean, 1.075? Am I misinterpreting anything here? Is there any way to correct this?

Leadwort

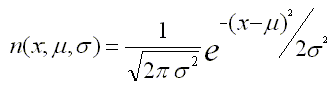
I actually did, @talonmies. The norm.pdf by itself is used for standardized random variables, hence it calculates exp(-x**2/2)/sqrt(2*pi). To bring mu and sigma into the relation, loc and and scale are introduced respectively. Specifying these would mean replacing x with (x-loc)/scale and dividing the final result by scale thus forming the Gaussian PDF as prescribed above. – Lombok

Answer 1

It's not a bug. It's not an incorrect result either. Probability density function's value at some specific point does not give you probability; it is a measure of how dense the distribution is around that value. For continuous random variables, the probability at a given point is equal to zero. Instead of p(X = x), we calculate probabilities between 2 points p(x1 < X < x2) and it is equal to the area below that probability density function. Probability density function's value can very well be above 1. It can even approach to infinity.

Metacarpal

@ÉbeIsaac to add a point to the answer INTEGRAL of PDF over the interval is equal to 1. But PDF itself might be above 1, below 1, 0. Cannot be negative, of course. – Minetta

As a general point, I think most introductory (college level) probability and statistics textbooks do not discuss these issues, and without some exposure to real analysis/measure/Riemann-sums it is not easy to develop an intuition. I found this to be a painless intro: statsathome.com/2017/06/26/… – Ungley

Answer 2

it's a density function, not a mass function

if variance is less than 1/(2*pi), the gaussian will exceed 1.0

exceeding 1 is only a limitation for mass functions, not density functions

Unalloyed

Answer 3

Probability density is the rate of change in cumulative probability. So where cumulative probability is increasing rapidly, density can easily exceed 1. But if we calculate the area under the density function, it will never exceed 1. Such areas are also called probability mass.

Using your example :

from statistics import mean, stdev        
import numpy as np


x, dx = np.linspace(0.3, 1.75, 1000, retstep=True)
mean_1, sigma_1 = mean(x), stdev(x)
f = np.exp(-((x-mean_1)/sigma_1)**2/2) / sigma_1 / np.sqrt(2 * np.pi)
print(np.sum(f)*dx)

Outputs 0.916581457225367

Credits to Richard McElreath in his book "statistical rethinking"

Gulledge