Effect of variance (sigma) at Gaussian smoothing

Question

I know about Gaussian, variance, and image blurring, and I think that I understood the concept of variance at Gaussian blur, but still I am not 100% sure.

I just want to know the role of sigma or variance in Gaussian smoothing. I mean, what happens by increasing the value of sigma for the same window size, and why does it happen?

It would be really helpful if somebody provide some nice literature about it. (I already tried few but couldn't find what i am looking for)

Major confusion:

Higher frequency -> details (e.g. noise),

Lower Frequency -> kind of overview of the image.

By increasing the sigma, we are allowing some higher frequencies, so we should get more detailed with increasing frequency. But the case is opposite! When we increase the sigma, the image becomes more blurry.

Rickierickman

Sigma is the variance (i.e. standard deviation squared). If you increase standard deviation in normal distribution, the distribution will be more spread out, and the peak will be less spiky. Similarly in gaussian smoothing, which is a low pass filter, it makes everything blurry, by de-emphasising sharp gradient changes in the image, thus if you increase the variance / stddev, it will be more blurry. But this is limited by the size of your gaussian kernel. – Dg

Here's a sample video of Gaussian blur with kernel(window) size of 105, and sigma that varies from 1.0 to 15.0: youtube.com/watch?v=A_MloE8B5Oo – Dg

@sub_o: Thanks, the video shows the effect of sigma which i have seen myself as well. But i am confused about the concept. Please have a look at my updated question in which i have updated my confusion. – Rickierickman

Ah the sigma we're talking here is not the one in frequency domain. It's inverse proportional to frequency. Look here: en.wikipedia.org/wiki/Gaussian_filter#Digital_implementation That might be where the confusion comes from – Dg

Answer 1

I think it should be done in the following steps, first from the signal processing point of view:

1. Gaussian Filter is a low pass filter. Low pass filters as their names imply pass low frequencies - keeping low frequencies. So when we look at the image in the frequency domain the highest frequencies happen in the edges(places that there is a high change in intensity and each intensity value corresponds to a specific visible frequency).
2. The role of sigma in the Gaussian filter is to control the variation around its mean value. So as the Sigma becomes larger the more variance allowed around mean and as the Sigma becomes smaller the less variance allowed around mean.
3. Filtering in the spatial domain is done through convolution. it simply means that we apply a kernel on every pixel in the image. The law exists for kernels. Their sum has to be zero.

Now putting all together! When we apply a Gaussian filter to an image, we are doing a low pass filtering. But as you know this happen in the discrete domain(image pixels). So we have to quantize our Gaussian filter in order to make a Gaussian kernel. In the quantization step, as the Gaussian filter(GF) has a small sigma it has the steepest pick. So the more weights will be focused in the center and the less around it.

In the sense of natural image statistics! The scientists in this field of studies showed that our vision system is a kind of Gaussian filter in the responses to the images. see for example take a look at a broad scene! don't pay attention to a specific point! so you see a broad scene with lots things in it. but the details are not clear! Now see a specific point in that seen. you see more details that previously you didn't. This is the Sigma appear here. when you increase the sigma you are looking to the broad scene without paying attention to the details exits. and when you decrease the value you will get more details.

I think Wikipedia can help more than me, Low Pass Filters, Guassian Blur

Heteronomous

I have got another confusion. Higher frequency-> details (e.g. noise), Lower Frequency-> kind of overview of the image. By increasing sigma, we are allowing some higher frequencies....so we should get more detailed with increasing frequency but the case is opposite, when we increase sigma, the image becomes more blurry. – Rickierickman

The edges in the image show themselves in higher frequencies(rapid changes in the intensity spatially) also noises(noise in the image means unwanted changes of intensities). The lower frequencies mean there is not a lot of changes in intensity. I said, as you increase sigma you will get a broad overview because the details vanished; we get a blurred image. That kind of rapid changes(high frequencies) become smoother. As we decrease the sigma we get more details. – Heteronomous

I suggest you to try some smoothing by gaussian filter in matlab or opencv. Plot its fft to see what happen to frequency domain before and after the smoothing. – Heteronomous

thank you so much @hadi to explain it well. I will say little about sigma which is standard deviation shows spread. if you spread a cone.. add more points to this cone peak,, it will lose its original shape.. mean will blur or smooth the original peak. sigma shows variation or spread at a peak.. more spread.. smooth that peak (broad overview, no detail or clear peak).. less spread.. less smoothing.. no spread.. no smoothing.. (clear peak which is detail of cone) – Nymphomania

This answer makes no sense. Discretization and quantization have nothing to do with any of this, the same is true in the continuous domain. And I don’t see any actual explanation for why you get a blurrier result when the sigma is larger! – Splayfoot

Answer 2

Put simply, increasing the sigma terms will cast a broader net over the neighboring pixels and decrease the impact of the pixels nearest the pixel of interest, e.g. it makes a blurrier image.

Cray

Answer 3

Usually we name the filter with the spatial response function. So the Gaussian filter means the spatial response is a Gaussian function.

However, the frequency response of GF is still Gaussian function with the relationship of sigma_f = 1/(2*pi*sigma_spatial)

Thus, the smaller the sigma_f the narrower the passband (the lower the cutoff frequency).

The sigma value in OpenCV is the spatial sigma used to generate the Gaussian kernel. Thus it has the inverted relationship with the passband.

The higher the sigma_spatial the lower the cutoff frequency.

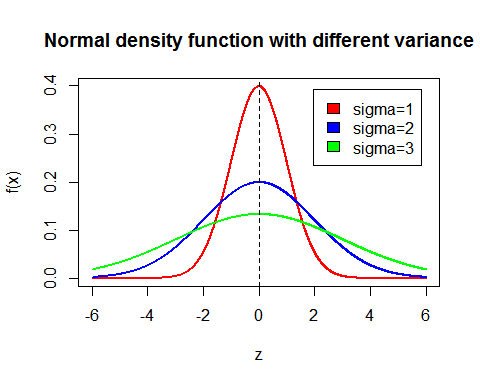
We can also directly view this in spatial operation perspective. We can treat the spatial filter as weighted average. The GF give the centre pixel more weight than the edge. The higher the sigma_spatial the wider the Gaussian, then the higher the weights on the edge. Thus the higher the sigma_spatial more detail get lost during the average.

People usually attempt to choose sigma for digital GF. However, for optimal effect, the sigma and the kernel size are not freely choosable. They actually depend on each other.

For quality, we do not want the kernel size to be too small. We would like the filter value at the kernel edge to be very close to 0, otherwise, there is much part of the bell shape is not in use.

For efficiency, we do not want the kernel size to be too big. If the kernel size is too big for chosen sigma, then most part of the kernel has filter parameters close to 0.

If we review the Gaussian function, we knew that if we choose a kernel size of 6*sigma, and the parameter at the centre is 1.0; then the value at the edge will be around 0.01

So in practice, usually, we do not specify the sigma at all. We normally just specify the kernel size and automatically get sigma = size/6

Maloney

This is a good answer (especially compared to the incongruent, rambling mess of misunderstandings and guesses that is the accepted answer). But in the last paragraph, I wouldn’t recommend to choose a filter size and compute the sigma from it, but do it the other way. The size must be rounded to an odd integer, so has much less precision when choosing it. The sigma can be any (sufficiently large) floating point number. There are for example scale spaces where you might want to multiply the sigma by sqrt(2) for every next level, you can’t do that when working with the size first. – Splayfoot