Fitting a curve to a power-law distribution with curve_fit does not work

Question

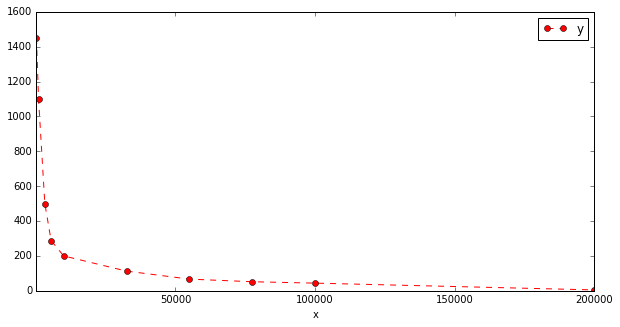
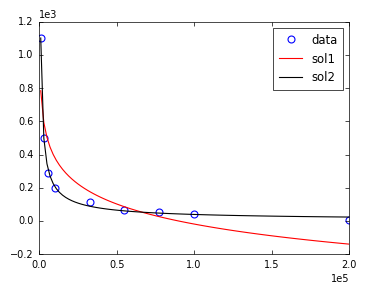
I am trying to find a curve fitting my data that visually seem to have a power law distribution.

I hoped to utilize scipy.optimize.curve_fit, but no matter what function or data normalization I try, I am getting either a RuntimeError (parameters not found or overflow) or a curve that does not fit my data even remotely. Please help me to figure out what I am doing wrong here.

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

df = pd.DataFrame({
            'x': [ 1000, 3250, 5500, 10000, 32500, 55000, 77500, 100000, 200000 ],
            'y': [ 1100, 500, 288, 200, 113, 67, 52, 44, 5 ]
        })
df.plot(x='x', y='y', kind='line', style='--ro', figsize=(10, 5))

def func_powerlaw(x, m, c, c0):
    return c0 + x**m * c

target_func = func_powerlaw

X = df['x']
y = df['y']

popt, pcov = curve_fit(target_func, X, y)

plt.figure(figsize=(10, 5))
plt.plot(X, target_func(X, *popt), '--')
plt.plot(X, y, 'ro')
plt.legend()
plt.show()

Output

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
<ipython-input-243-17421b6b0c14> in <module>()
     18 y = df['y']
     19 
---> 20 popt, pcov = curve_fit(target_func, X, y)
     21 
     22 plt.figure(figsize=(10, 5))

/Users/evgenyp/.virtualenvs/kindle-dev/lib/python2.7/site-packages/scipy/optimize/minpack.pyc in curve_fit(f, xdata, ydata, p0, sigma, absolute_sigma, check_finite, bounds, method, **kwargs)
    653         cost = np.sum(infodict['fvec'] ** 2)
    654         if ier not in [1, 2, 3, 4]:
--> 655             raise RuntimeError("Optimal parameters not found: " + errmsg)
    656     else:
    657         res = least_squares(func, p0, args=args, bounds=bounds, method=method,

RuntimeError: Optimal parameters not found: Number of calls to function has reached maxfev = 800.

Millican

Answer 1

As the traceback states, the maximum number of function evaluations was reached without finding a stationary point (to terminate the algorithm). You can increase the maximum number using the option maxfev. For this example, setting maxfev=2000 is large enough to successfully terminate the algorithm.

However, the solution is not satisfactory. This is due to the algorithm choosing a (default) initial estimate for the variables, which, for this example, is not good (the large number of iterations required is an indicator of this). Providing another initialization point (found by simple trial and error) results in a good fit, without the need to increase maxfev.

The two fits and a visual comparison with the data is shown below.

x = np.asarray([ 1000, 3250, 5500, 10000, 32500, 55000, 77500, 100000, 200000 ])
y = np.asarray([ 1100, 500, 288, 200, 113, 67, 52, 44, 5 ])

sol1 = curve_fit(func_powerlaw, x, y, maxfev=2000 )
sol2 = curve_fit(func_powerlaw, x, y, p0 = np.asarray([-1,10**5,0]))

Xanthin

thank you for your help and explanation. I've tried increasing maxfev, but on my machine 2,000 was not enough and I didn't increase it much further thinking that the problem was somewhere else. I haven't tried setting an initial estimate though and it does work like a charm. – Millican

When I have tried the answer I got a ValueError from the power operator in the func_powerlaw function. Changing p0 to np.asarray([0,10**5,0] solves this – Inexpugnable

Answer 2

Your func_powerlaw is not strictly a power law, as it has an additive constant.

Generally speaking, if you want a quick visual appraisal of a power law relation, you would

plot(log(x),log(y))

or

loglog(x,y)

Both of them should give a straight line, although there are subtle differences among them (in particular, regarding curve fitting).

All this without the additive constant, which messes up the power law relation.

---

If you want to fit a power law that weighs data according to the log-log scale (typically desirable), you can use code below.

import numpy as np
from scipy.optimize import curve_fit

def powlaw(x, a, b) :
    return a * np.power(x, b)
def linlaw(x, a, b) :
    return a + x * b

def curve_fit_log(xdata, ydata) :
    """Fit data to a power law with weights according to a log scale"""
    # Weights according to a log scale
    # Apply fscalex
    xdata_log = np.log10(xdata)
    # Apply fscaley
    ydata_log = np.log10(ydata)
    # Fit linear
    popt_log, pcov_log = curve_fit(linlaw, xdata_log, ydata_log)
    #print(popt_log, pcov_log)
    # Apply fscaley^-1 to fitted data
    ydatafit_log = np.power(10, linlaw(xdata_log, *popt_log))
    # There is no need to apply fscalex^-1 as original data is already available
    return (popt_log, pcov_log, ydatafit_log)

Anya