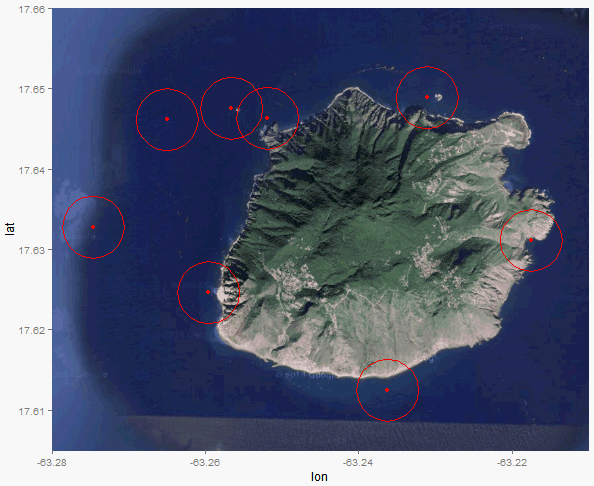
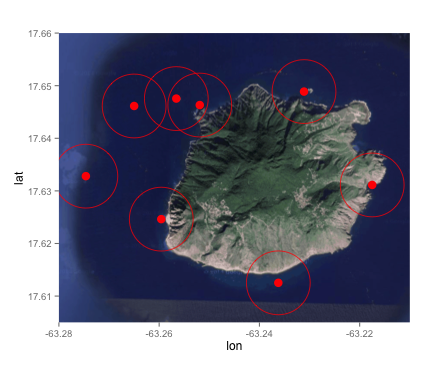
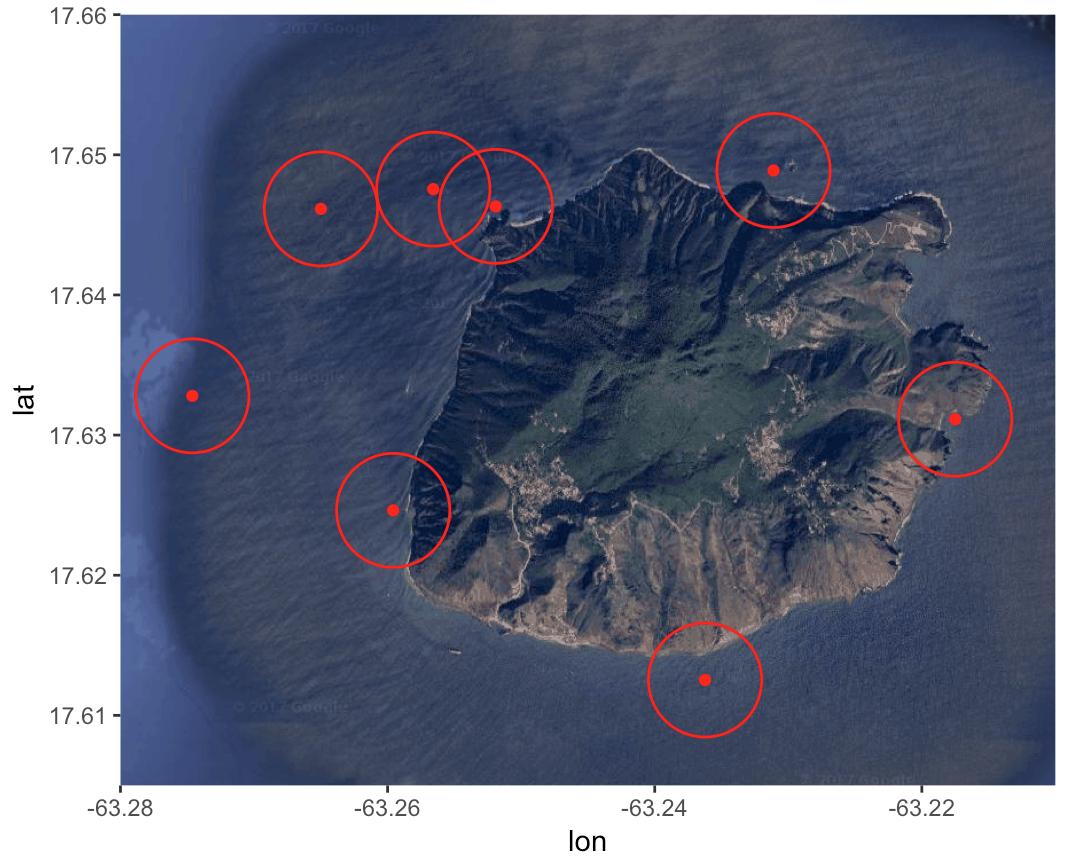
I have a map with the 8 points plotted on it:
library(ggplot2)
library(ggmap)
data = data.frame(
ID = as.numeric(c(1:8)),
longitude = as.numeric(c(-63.27462, -63.26499, -63.25658, -63.2519, -63.2311, -63.2175, -63.23623, -63.25958)),
latitude = as.numeric(c(17.6328, 17.64614, 17.64755, 17.64632, 17.64888, 17.63113, 17.61252, 17.62463))
)
island = get_map(location = c(lon = -63.247593, lat = 17.631598), zoom = 13, maptype = "satellite")
islandMap = ggmap(island, extent = "panel", legend = "bottomright")
RL = geom_point(aes(x = longitude, y = latitude), data = data, color = "#ff0000")
islandMap + RL + scale_x_continuous(limits = c(-63.280, -63.21), expand = c(0, 0)) + scale_y_continuous(limits = c(17.605, 17.66), expand = c(0, 0))
Now I want to plot a circle around each of the 8 plotted locations. The circle has to have a radius of 450 meters.
This is what I mean, but then using ggplot: https://gis.stackexchange.com/questions/119736/ggmap-create-circle-symbol-where-radius-represents-distance-miles-or-km
How can I achieve this?