How to find Strongly Connected Components in a Graph?

Question

I am trying self-study Graph Theory, and now trying to understand how to find SCC in a graph. I have read several different questions/answers on SO (e.g., 1,2,3,4,5,6,7,8), but I cant find one with a complete step-by-step example I could follow.

According to CORMEN (Introduction to Algorithms), one method is:

1. Call DFS(G) to compute finishing times f[u] for each vertex u
2. Compute Transpose(G)
3. Call DFS(Transpose(G)), but in the main loop of DFS, consider the vertices in order of decreasing f[u] (as computed in step 1)
4. Output the vertices of each tree in the depth-first forest of step 3 as a separate strong connected component

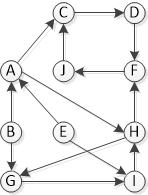
Observe the following graph (question is 3.4 from here. I have found several solutions here and here, but I am trying to break this down and understand it myself.)

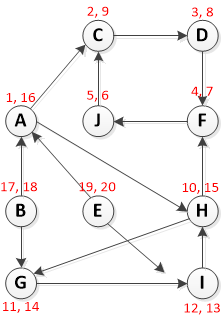
Step 1: Call DFS(G) to compute finishing times f[u] for each vertex u

Running DFS starting on vertex A:

Please notice RED text formatted as [Pre-Vist, Post-Visit]

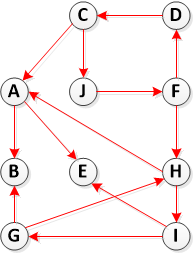
Step 2: Compute Transpose(G)

Step 3. Call DFS(Transpose(G)), but in the main loop of DFS, consider the vertices in order of decreasing f[u] (as computed in step 1)

Okay, so vertices in order of decreasing post-visit(finishing times) values:

{E, B, A, H, G, I , C, D, F ,J}

So at this step, we run DFS on G^T but start with each vertex from above list:

• DFS(E): {E}
• DFS(B): {B}
• DFS(A): {A}
• DFS(H): {H, I, G}
• DFS(G): remove from list since it is already visited
• DFS(I): remove from list since it is already visited
• DFS(C): {C, J, F, D}
• DFS(J): remove from list since it is already visited
• DFS(F): remove from list since it is already visited
• DFS(D): remove from list since it is already visited

Step 4: Output the vertices of each tree in the depth-first forest of step 3 as a separate strong connected component.

So we have five strongly connected components: {E}, {B}, {A}, {H, I, G}, {C, J, F, D}

This is what I believe is correct. However, solutions I found here and here say SCCs are {C,J,F,H,I,G,D}, and {A,E,B}. Where are my mistakes?

Mapel

Look a B and E: both have an indegree of zero and form a (degenerate) SCC all by themselves. I think the linked answers to be wrong. (beat me by 40 secs.) – Sestos

I believe the answers given in the sources you provide are wrong although both implementations are correct. I have implemented the algorithm that they are using and my algorithm gives me the answer you reached to. I guess they've comitted a mistake some where, but the algorithm isn't wrong. neither yours nor theirs. – Acerbate

FYI, for all who are interested, this is called Kosaraju’s algorithm. – Chiapas

Answer 1

Your steps are correct and your answer is also correct, by examining the other answers you provided you can see that they used a different algorithm: First you run DFS on G transposed and then you run an undirected components algorithm on G processing the vertices in decreasing order of their post numbers from the previous step.

The problem is they ran this last step on G transposed instead of in G and thus got an incorrent answer. If you read Dasgupta from page 98 onwards you will see a detailed explanation of the algorithm they (tried) to use.

Josuejosy

Answer 2

Your answers is correct. As per CLRS, "A strongly connected component of a directed graph G = (V,E) is a maximal set of vertices C, such that for every pair of vertices u and v, we have both u ~> v and v ~> u, i.e. vertices v and u are reachable from each other."

In case you assume {C, J, F, H, I, G, D} as correct, there is no way to reach from D to G (amongst many other fallacies), and same with other set, there is no way to reach from A to E.

Legitimate