Please explain murmur hash? [closed]

Question

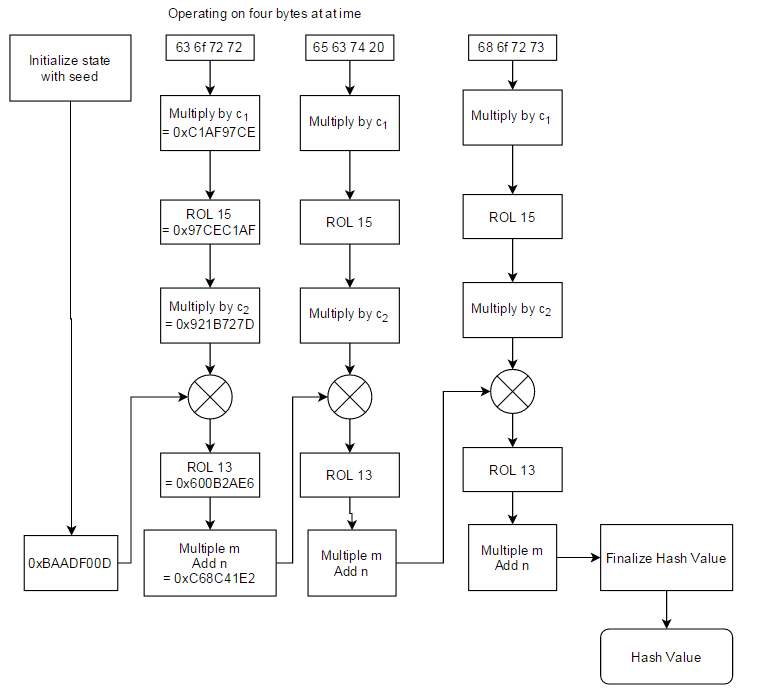
I just found out murmur hash, seems to be the fastest known and quite collision resistant. I tried to dig more about the algorithm or implementation in full source code, but I am having difficulty understanding it. Could someone here explain the algorithm used, or implement it in full source code, preferably in C. I read the C source code from the author website but has no idea, like: What is seed, h, k, m?

What does this mean? :

k *= m; 
k ^= k >> r; 
k *= m; 
    
h *= m; 
h ^= k;

data += 4;
len -= 4;

Reference : http://murmurhash.googlepages.com/

Kuching

Have you looked at wikipedia? en.wikipedia.org/wiki/MurmurHash – Combined

Answer 1

The code is available here . m and r are constants used by the algorithm. k *= m means take variable k and multiple it by m. k ^= k >> r means take k and right shift the bits r places (e.g. if r is 2 110101 would become 001101) and then XOR it with k.

Hope that gives you enough to work through the rest.

Regards

Confederate

Answer 2

The best explanation of the Murmur algorithm is on the Murmur Hash Wikipedia page:

Murmur3_32(key, len, seed)
    //Note: In this version, all integer arithmetic is performed 
    //with unsigned 32 bit integers. In the case of overflow, 
    //the result is constrained by the application 
    //of modulo 232 arithmetic.

    c1 ← 0xcc9e2d51
    c2 ← 0x1b873593
    r1 ← 15
    r2 ← 13
    m ← 5
    n ← 0xe6546b64

    hash ← seed

    for each fourByteChunk of key
        k ← fourByteChunk

        k ← k × c1
        k ← (k ROL r1)
        k ← k × c2

        hash ← hash XOR k
        hash ← (hash ROL r2)
        hash ← hash × m + n

    with any remainingBytesInKey
        remainingBytes ← SwapEndianOrderOf(remainingBytesInKey)
        // Note: Endian swapping is only necessary on big-endian machines.

        remainingBytes ← remainingBytes × c1
        remainingBytes ← (remainingBytes ROL r1)
        remainingBytes ← remainingBytes × c2

        hash ← hash XOR remainingBytes

    hash ← hash XOR len

    hash ← hash XOR (hash SHR 16)
    hash ← hash × 0x85ebca6b
    hash ← hash XOR (hash SRH 13)
    hash ← hash × 0xc2b2ae35
    hash ← hash XOR (hash SHR 16)

And my own:

Dateless

That's code. True, quite readable pseudo code, but I still don't understand the ''explanation". I get what the steps are doing, could write it in several languages, but don't get what each step contributes to the hash, like, mathematically and stuff. (I'm still looking around for a good explanation; not attacking this answer or anything). – Reproachless

@Reproachless What about the pretty picture i just added? – Dateless

Well, it tells nothing about mathematical properties in a way that I can understand... But I'm probably getting ahead of myself; the diagram did help me to write a version without looking at an actual implementation, more than the pseudo-code, so thanks ;) – Reproachless

The following link will give you some insight into the though process of the author: sites.google.com/site/murmurhash – Khalif

first computation column on the figure: multiplication of 636f7272 and cc9e2d51 overflows 32 bits and when mod32 applied yields 87bd4012, not 0xC1AF97CE... right? – Lietman

@Lietman not only that, the ROL by 15 is incorrect as well :(. – Psalmbook