Extending minimax algorithm for multiple opponents

Question

The minimax algorithm is well described for two players for games like tic-tac-toe. I need to write an AI for a Tank game. In this game the tanks have to move in a maze that have obstacles in the form of walls. The goal is to collect coin piles. If it was only two players the minimax algorithm can be implemented. But how to implement it for more than two? As at each turn each player will try to maximize his own winning edge. I can not think of all the players as one enemy trying to reduce only my winning edge creating the two player levels as in the original minimax algorithm. Please excuse me if the question is not in good format. Still new to this forum

Brockbrocken

Answer 1

You can no longer use minimax for this. Unless you make a hybrid goal of maximizing one's profits and minimizing the sum of the other's profits. But this is very hard to implement.

Better is to create algorithms able to learn on a strategical level what needs to be done. Transform the game into a two player one: me vs. the others and start from here.

Dishonorable

thank you for the feedback. can not up vote yet. :). I was thinking on the line of extending A* algorithm. – Brockbrocken

Hey you are on coding game right ? Did you apply this to the Tron Battle ? – Cookhouse

Nop :) I mean, I am there but I haven't applied it. – Dishonorable

Answer 2

Mihai Maruseac is only partially right with saying that MiniMax cannot be used anymore. If "MiniMax" refers to the "standard variant" of MiniMax then he is perfectly right! (And this is what he meant.) However, you can also regard MiniMax as MaxiMax, where two players maximize their own reward each (this is exactly what AlphaWolf wrote in the question). The generalization to n players is thus called Max^n, which can still be regarded MiniMax, somehow. Anyway, below I explain why the standard 2-player MiniMax can indeed not be used in a multiplayer setting with 3 players or more. Then, finally, I give references to the correct alternative, i.e., the Max^n algorithm.

So let's first consider whether one can simply turn 2-player MiniMax into an n-player MiniMax by considering all opponents as Min-Players, i.e., they will all try to minimize the reward of the MAX player.

Well, you cannot! Let me explain why.

First, recall that MiniMax is always exclusively considering 2-player zero-sum games. As a consequence, MiniMax is usually always described with only a single game outcome. However, technically, there are two! That of the MAX player and that of the MIN player. So, to be super-formally correct, one would have to give a 2-tuple as game outcome per search node, say (payoff-P1,payoff-P2), with payoff-P1 being the outcome for P1 (MAX) and payoff-P2 being the outcome for P2 (MIN). However, since we usually consider zero-sum games, we know that their sum always equals zero, i.e., payoff-P1 + payoff-P2 = 0. Thus, we can always infer the win of the other and hence only represent the outcome from P1's perspective. Furthermore, minimizing payoff-P2 is the the same maximizing payoff-P1.

For almost all the games (except in real-life when psychological factors come into play, say revenge without caring for your own loss) we always assume that all agents play rational. This is going to be very important later when we talk about more than two players! What is rationality? Every player aims at maximizing their own reward(!) again assuming that all other players play rational as well.

Back to 2-player zero-sum: We did exploit/assume rationality because P1 (MAX) was already maximizing its reward anyway (by definition), and MIN was also maximizing its own reward, because it was minimizing that of MAX (which is, because of zero-sum the same as maximizing MINs reward). Thus, both players were maximizing their own reward and hence played rational.

Now let's assume we have more than 2 players, say 3 for simplicity.

Not let's see whether we could simply replace all opponents by MIN players (this is suggested sometimes, so I found it useful from a didactic point of view). If we do that, both only minimize the reward of the MAX player, whereas MAX continues to maximize its own. What this means semantically, though, is a collaboration of the two enemies against MAX. This collaboration breaks with our assumption of rationality, i.e., the players are not maximizing their own rewards anymore! (So, minimizing MAX's reward is only equivalent to maximizing one's own reward when there are two players, not if there are more than that.) I give an example to illustrate that:

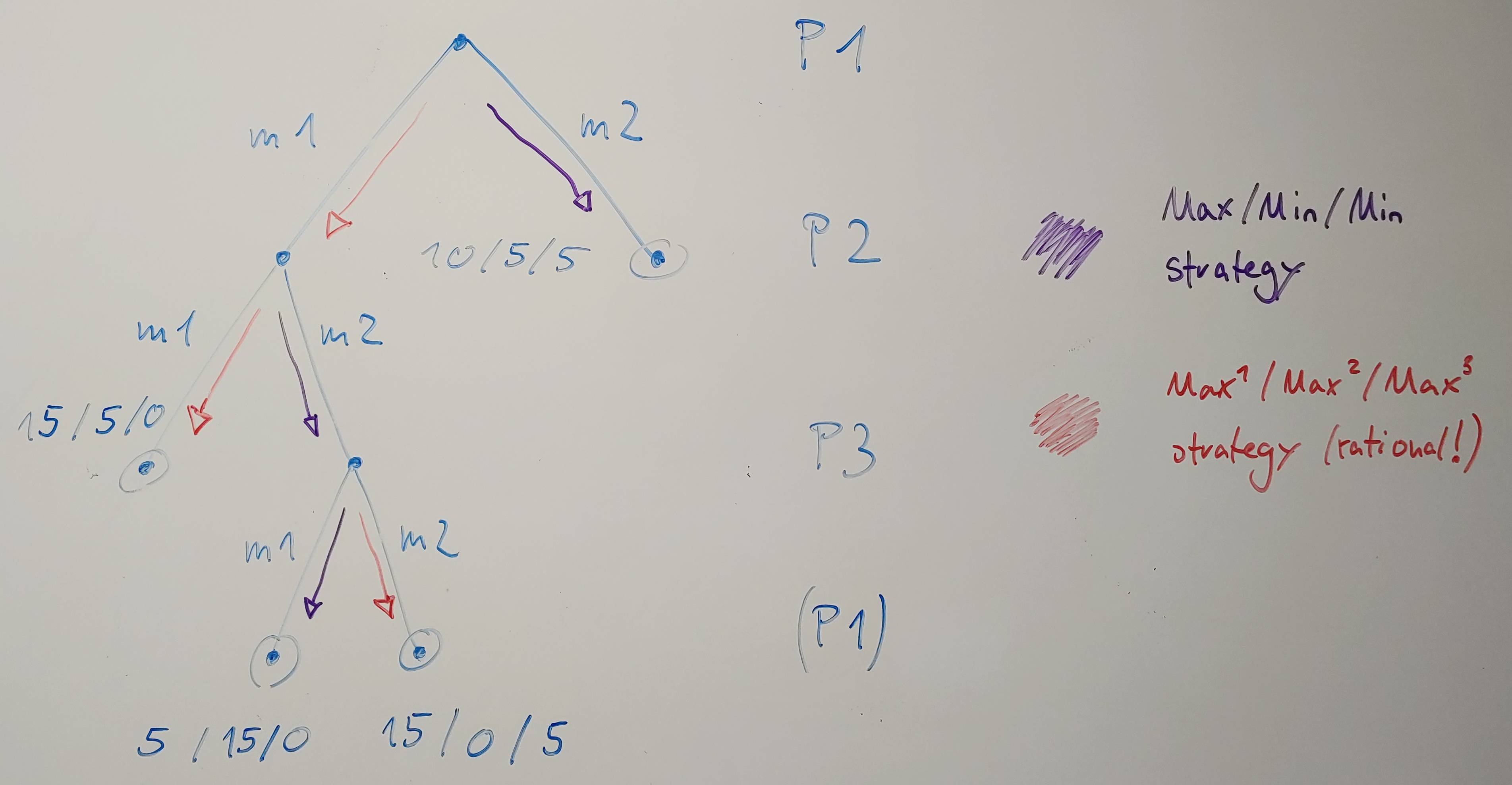
What we see here is the following:

• We have, as usual, a game tree, where three players (P1,P2,P3) take alternating turns. Every player has two turns. At the latest the game ends after 3 moves (technically, P1 would have to make a turn, then, but both states are final/leafs, so the game ends instead). The game describes a 3-player zero-sum game (although zero-sum is not required anymore! everything described also works without this assumption!).
• The maximal win is 20, distributed among the 3 players. (Note that in my version all wins are positive. However, it is still a zero-sum as all wins sum up to exactly the same value, so it could easily be transformed into one where they all add up to zero all the time.) The wins are shown as tuples "payoff-P1 / payoff-P2 / payoff-P3".
• Furthermore, I showed the pursed strategies by the respective players in two different colors: Purple is the strategy pursued by assuming only P1 is a MAX player and the others only minimize its reward (without caring for the own reward). Red shows the rational strategy assuming that all players are MAX players, i.e., maximizing their own reward.

So what happens in this game if P2 and P3 are considered MIN players? They would minimize P1s's reward, so P1 assumes it will receive only 5 when playing m1, because P2 can minimize P1's reward by playing m2. Thus P1 will choose its second move m2 winning (only) 10.

This assumption of both opponents being MIN players can however be regarded a collaboration of the two players (which is not rational). Because, when assuming rationality, player P2 would never play m2, because P3 would actually play m3 (so that P3 wins 5 instead of 0). But assuming that all opponents minimize P1 will make P2 pick m2, because that enables P3 to play m1 thus reducing P1's win to 5 (instead of 15 if P3 would have played rational). So, using a MAX/MIN/MIN strategy enables to find (or assume) strategies in which opponents collaborate against P1/MAX, which in reality (assuming rationality) would never happen! So that MiniMax adaptation to more than 2 players is clearly wrong. (I.e., overly pessimistic in a sense of detecting cases that would just never happen.) We can see in the figure that, when assuming rational agents, P1 should play m1 instead m2, thus winning 15 instead of only 10.

This was to show that MiniMax has to be extended in a different way.

How should be obvious: Simply represent the outcome for each player separately with a vector as described above. And instead of either maximizing or minimizing depending on who has its turn, we always maximize the current's player outcome. The resulting algorithm is thus also referred to as Max^n for n players. Again, note that MiniMax is thus just Max^2 with the tuple (payoff-P1,payoff-P2), where payoff-P2 is defined as -payoff-P1.

The Max^n algorithm was described by C.A. Luckhardt and K.B. Irani in "An algorithmic solution of N-person games", Proceedings of the Fifth National Conference on Artificial Intelligence (AAAI'86), p.158-162, AAAI Press. The paper is publicly available at: https://www.aaai.org/Papers/AAAI/1986/AAAI86-025.pdf

Note that MiniMax, and thus Max^n is never used in practice due to the exponential increase of the search space, i.e., game tree. Instead, one always uses Alpha/Beta pruning, which is a rather intuitive extension to never visit/explore branches of the tree that would be pointless to search anyway. Alpha/Beta was also extended to work for n-player games (n>2) as well, described by Richard Korf in "Multi-player alpha-beta pruning" in Artificial Intelligence 48 (1991), p.99-111. The article is publicly available at: https://www.cc.gatech.edu/~thad/6601-gradAI-fall2015/Korf_Multi-player-Alpha-beta-Pruning.pdf

Finally, let me add one very interesting observation: In 2-player zero-sum MiniMax, the strategy computed is "perfect" in the sense that it will definitely achieve at least the win that's guaranteed/computed by MiniMax. If the opponent plays irrational, i.e, deviates from its strategy, then the outcome can only be higher. In n-player zero-sum MiniMax, i.e., Max^n, this is not the case anymore! Recall that the rational strategy for P1 was to play m1 thus winning 15 (if the opponents play rational). However, if the opponents don't play rational, then pretty much everything can happen. Here, if P2 does irrationally play m2, then P1's output completely depends on what P3 does, so P1 could also win severely less. The reason for this is that in 2-player zero-sum the opponent's action directly influences one's own outcome -- and only that! But with 3 or more players, the wins can also be distributed among the other players as well.

Nevers

Interesting fact about MiniMax and Max^n: Apparently it was shown that there exist pathological cases where "searching deeper" (but not until the end of the game, as we would have perfect information, then) can cause the computed outcomes to decrease in value. This was shown by Dana Nau et al. for (2-player) MiniMax. Its generalization for Max^n was shown by D. Mutchler in "The multi-player version of minimax displays game-tree pathology" (AIJ 1993), see sciencedirect.com/science/article/pii/000437029390108N – Nevers

+1 but your answer is a bit misleading concerning alpha-beta-pruning. As the paper you've linked says: alpha-beta is not efficient for multi-player (n>2) games because only shallow pruning is possible. – Bib

Well, I didn't say it's efficient. :) (I wouldn't even know that.) I/we could add that comment if you think it's important enough. (I would assume it's not, but that's just my opinion.) – Nevers

Answer 3

How you handle minimizing function with multiple minimizing agents is to run a minimizing function, with the same depth for all the agents. Once the minimizing agents are all gone through, you run a maximizing function on the last minimizing agent.

# HOW YOU HANDLE THE MINIMIZING FUNCTION - If this pseudocode helps make better sense out of this.
scores = []
if agent == end_of_minimizing_agents: # last minimizing agent
    for actions in legal_actions: 
        depth_reduced = depth-1
        scores.append(max(successor_state, depth_reduced))
else:
    for actions in legal_actions: 
        scores.append(min(successor_state, depth))
bestScore = min(scores)
return bestScore

Gressorial