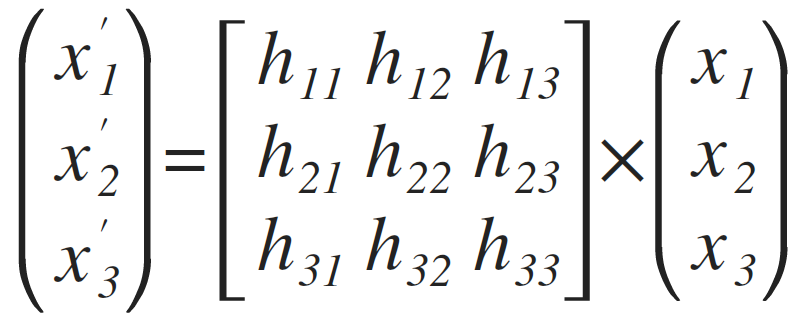Need better and simpler understanding of CATransform3D

Question

Please go through the images.

So this is the code which I got from some online source and it does transform my object. Besides that, I understood nothing at all. I am new to CATransform3D and want to know exactly how it works.

CATransform3D transform = CATransform3DIdentity;
transform.m34 = 1.0 / -500;
transform = CATransform3DRotate(transform, 45.0f * M_PI / 180.0f, 0, 1, 0.0f);
_bgView.layer.transform = transform;

I want to know how did this code run? Why did we set some value in m34? I found that its some kind of matrix which even confuses me more. Also, what do the arguments in the CATransform3DRotate mean???

I am trying to understand but not getting any further.

I want a deep understanding of CATransform3D. Please help with any articles, documentation or by explaining yourselves.

Thanks a lot.

Alphorn

Hmm, that code looks familiar. From fluffy's comment on my answer there: "FYI, the reason the m34 cell affects the perspective transform is that's the cell in the matrix that affects how the world-space Z value maps to the clip-space W value (which is used for perspective projection). Read up on homogenous transformation matrices for more information." – Woorali

How to rotate using touch point ? – Serotherapy

Answer 1

I'm not sure what m34 is without looking.

A 2D rotation is easy because all it needs is an angle by which to rotate. The rotation is then done AROUND the Z axis (i.e. the axis that points directly out of the screen).

A 3D rotation is different. It needs an angle but also it needs to know which axis (or axes) you are rotating around.

In CATransform3DRotate you give it five parameters...

1. The transform that you want to apply the rotation to.

2. Angle (in radians) π radians = 180 degrees 3, 4 and 5 are how much of the angle rotation to apply to each axis.

3. X axis - this is the axis that goes from the left of the screen to the right of the screen.

4. Y axis - this is the axis that goes from the top of the screen to the bottom of the screen.
5. Z axis - this is the axis that points directly out of the screen straight towards you.

The rotation you have applied in your example is as follows...

angle = 45 degrees (converted into radians). X = 0 Y = 1 Z = 0

This means that all of the 45 degrees will be rotated around the Y axis. i.e. it will rotate like a revolving door around the line down its middle.

If you had the params... "1, 0, 0" at the end then it would rotate like a paddle boat paddle. "Falling away from you."

Finally if you had "0, 0, 1" it would spin like a catherine wheel on the screen.

You can also combine the values i.e. have "0, 1, 1" to apply rotation about two axes.

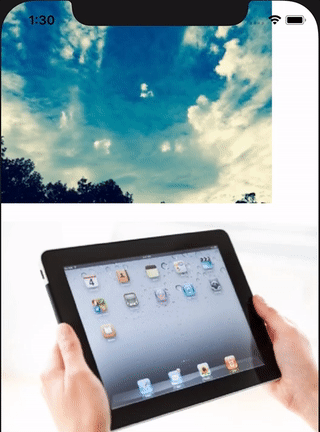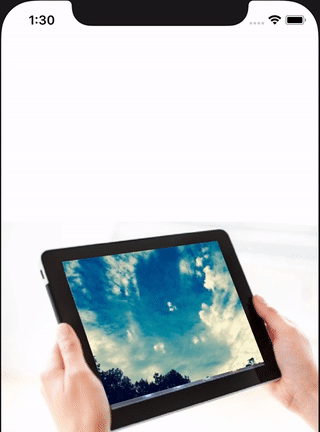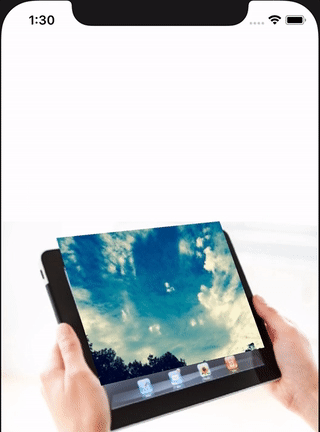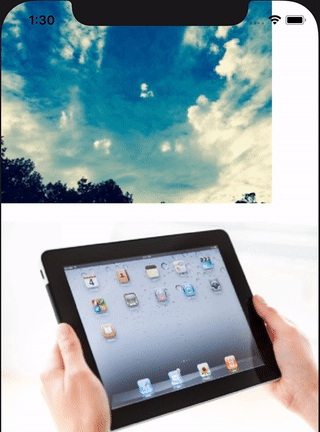
The w row of the matrix is the perspective projection. Did you ever do perspective drawing at school where you place a dot and draw lines from the dot and then draw things to fit those lines to give it perspective? Well the m34 value determines where that dot is placed and so provides perspective. Set it to something like -50 and you will see a bigger difference.

Setting m34 relates to the Z axis value of this point. So the point is placed at (0, 0, -1/500)

Peroration

Okay, that pretty much clears everything up! But still I wanted to know the matrix values. How do they play their role in this?? But anyways, thanks a lot for clearing up the remaining part! :) – Alphorn

No worries. The link in David's answer explains about the matrix value that you changed. en.wikipedia.org/wiki/… – Peroration

Okay, one more quick question. What if I would need to animate this transform? Will I need to increase/decrease the value of m34 in subsequent steps?? – Alphorn

Okay!! Maybe I get your point. And the origin (i.e 0,0,0) would be center of the object or it would be the bottom left corner of the screen??? – Alphorn

I think the origin is the bottom left (or possibly top left) but is sort of moot as there is no actual 3D space. Think of the coords as relative more than absolute. – Peroration

Okay. Still a bit confused, but much clearer than before! Thank you so much for your instant help! – Alphorn

Don't worry, it's not the easiest thing to get your head around. I'm still learning myself :D – Peroration

Answer 2

The m34 value is the third row, forth column and is the value in the matrix behind the transform that actually gives the rotation perspective.

You can read more about the math behind matrix multiplications on Wikipedia.

• Transformation matrix
• 3D Perspective

Regarding the values for CATransform3DRotate(...).

• The first argument is the transform that you are rotating
• The second is the angle (in radians),
• The other three arguments it's the axis you are rotating around ((x, y, z) vector).

Claritaclarity

Ah, I didn't know about the "w" row in the matrix. That clears it up for me, thanks :D – Peroration

Thanks for the help. Actually I went through both the links before posting here but it didn't help much! It still didn't clear up about how does this matrix work for any transformation. – Alphorn

Answer 3

Here is my project in Swift https://github.com/paulz/PerspectiveTransform that helps to calculate CATransform3D and includes Example app and playgrounds.

it can be used to animate CALayer transform property.

See wiki: https://github.com/paulz/PerspectiveTransform/wiki for details on constructing the matrix and other possible solutions.

Thank you for this question, it helped me to get started on my project knowing not only me have that problem!

Tanberg

Thank you, @pang did not mean to self promote. This is the article that inspired me to develop the solution, so want to bring it back. Now I see how this could be self promotion. – Tanberg