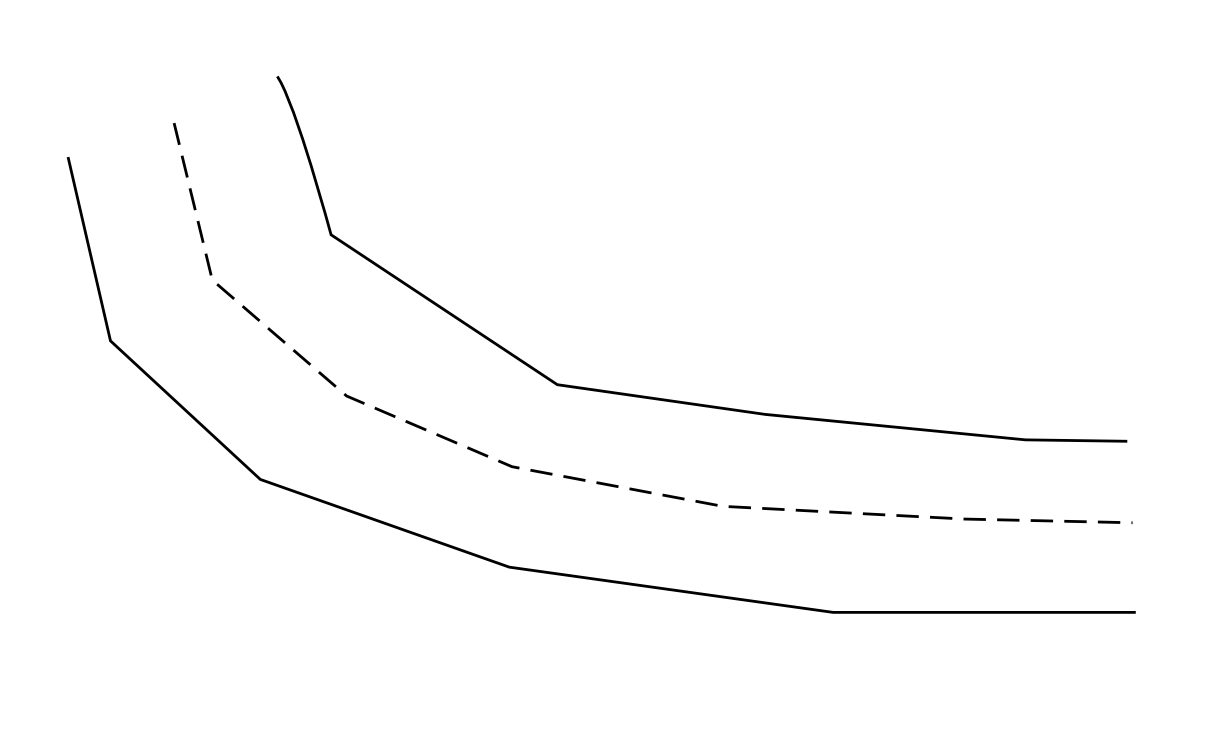
First of all, pardon the overkill; I had fun with your question. If the description is too long, feel free to skip to the bottom, I defined a function that does everything I describe.
Your problem would be relatively straightforward if your arrays were the same length. In that case, all you would have to do is find the average between the corresponding x values in each array, and the corresponding y values in each array.
So what we can do is create arrays of the same length, that are more or less good estimates of your original arrays. We can do this by fitting a polynomial to the arrays you have. As noted in comments and other answers, the midline of your original arrays is not specifically defined, so a good estimate should fulfill your needs.
Note: In all of these examples, I've gone ahead and named the two arrays that you posted a1 and a2.
Step one: Create new arrays that estimate your old lines
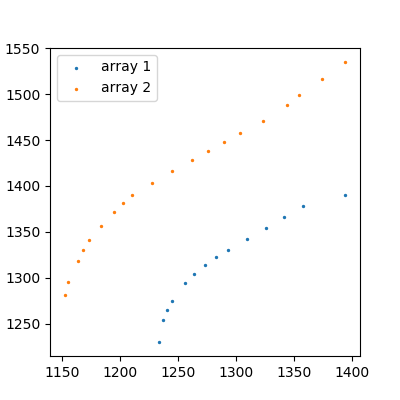
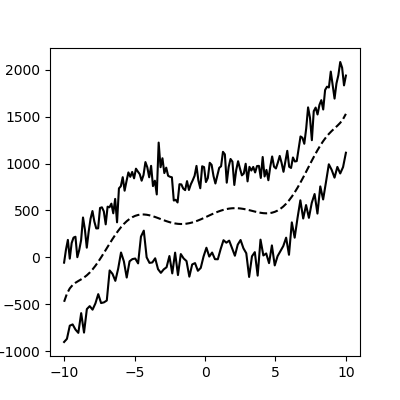
Looking at the data you posted:
![the data]()
These aren't particularly complicated functions, it looks like a 3rd degree polynomial would fit them pretty well. We can create those using numpy:
import numpy as np
# Find the range of x values in a1
min_a1_x, max_a1_x = min(a1[:,0]), max(a1[:,0])
# Create an evenly spaced array that ranges from the minimum to the maximum
# I used 100 elements, but you can use more or fewer.
# This will be used as your new x coordinates
new_a1_x = np.linspace(min_a1_x, max_a1_x, 100)
# Fit a 3rd degree polynomial to your data
a1_coefs = np.polyfit(a1[:,0],a1[:,1], 3)
# Get your new y coordinates from the coefficients of the above polynomial
new_a1_y = np.polyval(a1_coefs, new_a1_x)
# Repeat for array 2:
min_a2_x, max_a2_x = min(a2[:,0]), max(a2[:,0])
new_a2_x = np.linspace(min_a2_x, max_a2_x, 100)
a2_coefs = np.polyfit(a2[:,0],a2[:,1], 3)
new_a2_y = np.polyval(a2_coefs, new_a2_x)
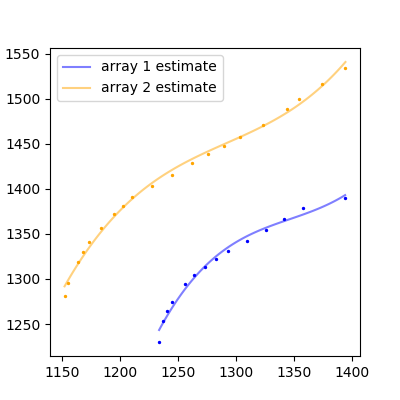
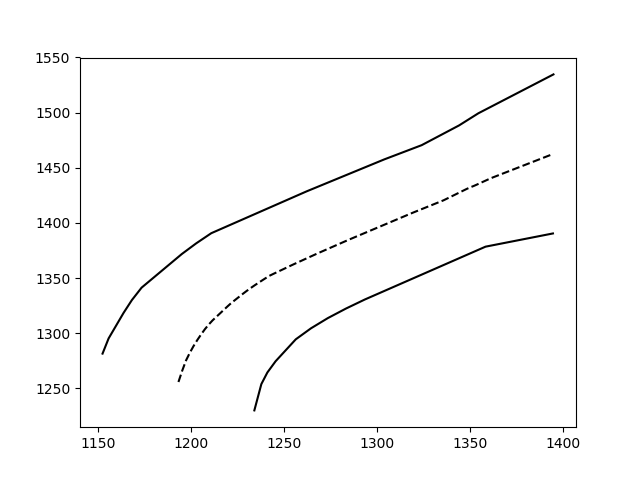
The result:
![Fitted Arrays]()
That's not bad so bad! If you have more complicated functions, you'll have to fit a higher degree polynomial, or find some other adequate function to fit to your data.
Now, you've got two sets of arrays of the same length (I chose a length of 100, you can do more or less depending on how smooth you want your midpoint line to be). These sets represent the x and y coordinates of the estimates of your original arrays. In the example above, I named these new_a1_x, new_a1_y, new_a2_x and new_a2_y.
Step two: calculate the average between each x and each y in your new arrays
Then, we want to find the average x and average y value for each of our estimate arrays. Just use np.mean:
midx = [np.mean([new_a1_x[i], new_a2_x[i]]) for i in range(100)]
midy = [np.mean([new_a1_y[i], new_a2_y[i]]) for i in range(100)]
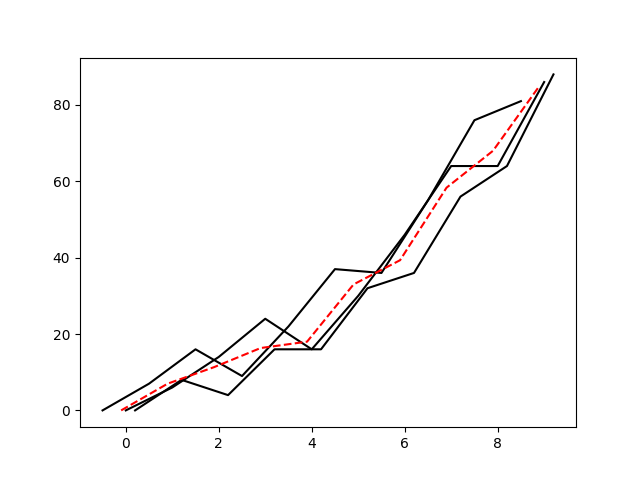
midx and midy now represent the midpoint between our 2 estimate arrays. Now, just plot your original (not estimate) arrays, alongside your midpoint array:
plt.plot(a1[:,0], a1[:,1],c='black')
plt.plot(a2[:,0], a2[:,1],c='black')
plt.plot(midx, midy, '--', c='black')
plt.show()
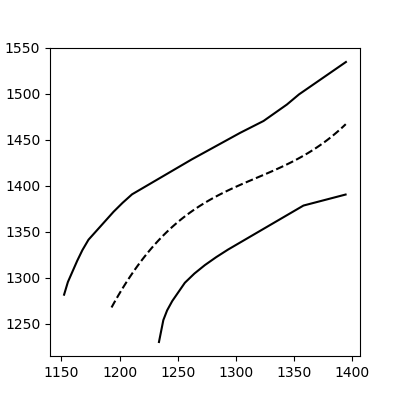
And voilà:
![final product]()
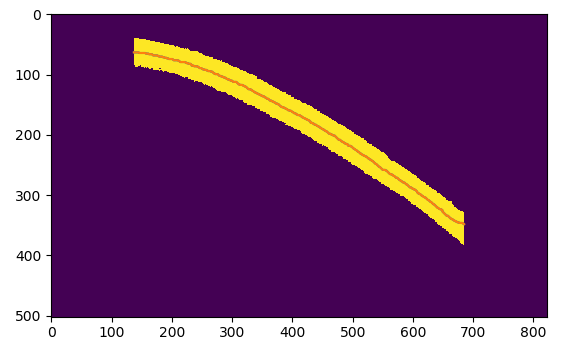
This method still works with more complex, noisy data (but you have to fit the function thoughtfully):
![noisy data]()
As a function:
I've put the above code in a function, so you can use it easily. It returns an array of your estimated midpoints, in the format you had your original arrays in.
The arguments: a1 and a2 are your 2 input arrays, poly_deg is the degree polynomial you want to fit, n_points is the number of points you want in your midpoint array, and plot is a boolean, whether you want to plot it or not.
import matplotlib.pyplot as plt
import numpy as np
def interpolate(a1, a2, poly_deg=3, n_points=100, plot=True):
min_a1_x, max_a1_x = min(a1[:,0]), max(a1[:,0])
new_a1_x = np.linspace(min_a1_x, max_a1_x, n_points)
a1_coefs = np.polyfit(a1[:,0],a1[:,1], poly_deg)
new_a1_y = np.polyval(a1_coefs, new_a1_x)
min_a2_x, max_a2_x = min(a2[:,0]), max(a2[:,0])
new_a2_x = np.linspace(min_a2_x, max_a2_x, n_points)
a2_coefs = np.polyfit(a2[:,0],a2[:,1], poly_deg)
new_a2_y = np.polyval(a2_coefs, new_a2_x)
midx = [np.mean([new_a1_x[i], new_a2_x[i]]) for i in range(n_points)]
midy = [np.mean([new_a1_y[i], new_a2_y[i]]) for i in range(n_points)]
if plot:
plt.plot(a1[:,0], a1[:,1],c='black')
plt.plot(a2[:,0], a2[:,1],c='black')
plt.plot(midx, midy, '--', c='black')
plt.show()
return np.array([[x, y] for x, y in zip(midx, midy)])
[EDIT]:
I was thinking back on this question, and I overlooked a simpler way to do this, by "densifying" both arrays to the same number of points using np.interp. This method follows the same basic idea as the line-fitting method above, but instead of approximating lines using polyfit / polyval, it just densifies:
min_a1_x, max_a1_x = min(a1[:,0]), max(a1[:,0])
min_a2_x, max_a2_x = min(a2[:,0]), max(a2[:,0])
new_a1_x = np.linspace(min_a1_x, max_a1_x, 100)
new_a2_x = np.linspace(min_a2_x, max_a2_x, 100)
new_a1_y = np.interp(new_a1_x, a1[:,0], a1[:,1])
new_a2_y = np.interp(new_a2_x, a2[:,0], a2[:,1])
midx = [np.mean([new_a1_x[i], new_a2_x[i]]) for i in range(100)]
midy = [np.mean([new_a1_y[i], new_a2_y[i]]) for i in range(100)]
plt.plot(a1[:,0], a1[:,1],c='black')
plt.plot(a2[:,0], a2[:,1],c='black')
plt.plot(midx, midy, '--', c='black')
plt.show()
![enter image description here]()