Catmull-Rom splines in python

Question

Is there a library or function in python to compute Catmull-Rom spline from three points ?

What I need in the end are the x,y coordinates of points along the spline, provided that they are always equidistant of a given amount t along the spline (say, the spline curve is 3 units long and I want the x,y coordinates at spline length 0, 1, 2 and 3)

Nothing really exciting. I am writing it by myself, but if you find something nice, It would be great for testing (or to save time)

Ima

Answer 1

3 points ? Catmull-Rom is defined for 4 points, say p_1 p0 p1 p2; a cubic curve goes from p0 to p1, and outer points p_1 and p2 determine the slopes at p0 and p1. To draw a curve through some points in an array P, do something like this:

for j in range( 1, len(P)-2 ):  # skip the ends
    for t in range( 10 ):  # t: 0 .1 .2 .. .9
        p = spline_4p( t/10, P[j-1], P[j], P[j+1], P[j+2] )
        # draw p

def spline_4p( t, p_1, p0, p1, p2 ):
    """ Catmull-Rom
        (Ps can be numpy vectors or arrays too: colors, curves ...)
    """
        # wikipedia Catmull-Rom -> Cubic_Hermite_spline
        # 0 -> p0,  1 -> p1,  1/2 -> (- p_1 + 9 p0 + 9 p1 - p2) / 16
    # assert 0 <= t <= 1
    return (
          t*((2-t)*t - 1)   * p_1
        + (t*t*(3*t - 5) + 2) * p0
        + t*((4 - 3*t)*t + 1) * p1
        + (t-1)*t*t         * p2 ) / 2

One can use piecewise quadratic curves through 3 points -- see Dodgson, Quadratic Interpolation for Image Resampling. What do you really want to do ?

Visitor

3 real points, plus the two obligatory endpoints for slope at the end – Ima

spline_4p( t, p_1, p0, p1, p2 ) goes p0 .. p1, then spline_4p( t, p0, p1, p2, p3 ) p1 .. p2, with p_1 and p3 affecting the slopes. Hth ? – Visitor

Great and working example! But in t-cycle we should cast t to float: p = spline_4p( float(t)/10, P[j-1], P[j], P[j+1], P[j+2] ) – Monopolize

Answer 2

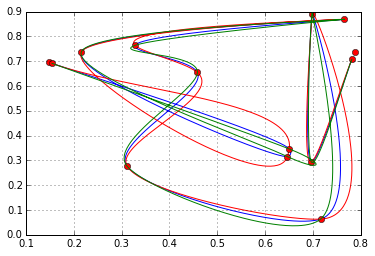
As mentioned previously you do need 4 points for catmull-rom, and the endpoints are an issue. I was looking at applying these myself instead of natural cubic splines (which the potential overshoots beyond the known data range is impractical in my application). Similar to @denis's code, here is something that might help you (notice a few things. 1) That code just randomly generates points, I'm sure you can use the commented out examples for how to use your own data. 2) I create extended endpoints, preserving the slope between the first/last two points - using an arbitrary distance of 1% of the domain. 3)I include uniform, centripetal, and chordial knot parameterization for comparison):

# coding: utf-8

# In[1]:

import numpy
import matplotlib.pyplot as plt
get_ipython().magic(u'pylab inline')


# In[2]:

def CatmullRomSpline(P0, P1, P2, P3, a, nPoints=100):
  """
  P0, P1, P2, and P3 should be (x,y) point pairs that define the Catmull-Rom spline.
  nPoints is the number of points to include in this curve segment.
  """
  # Convert the points to numpy so that we can do array multiplication
  P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])

  # Calculate t0 to t4
  alpha = a
  def tj(ti, Pi, Pj):
    xi, yi = Pi
    xj, yj = Pj
    return ( ( (xj-xi)**2 + (yj-yi)**2 )**0.5 )**alpha + ti

  t0 = 0
  t1 = tj(t0, P0, P1)
  t2 = tj(t1, P1, P2)
  t3 = tj(t2, P2, P3)

  # Only calculate points between P1 and P2
  t = numpy.linspace(t1,t2,nPoints)

  # Reshape so that we can multiply by the points P0 to P3
  # and get a point for each value of t.
  t = t.reshape(len(t),1)

  A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
  A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
  A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3

  B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
  B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3

  C  = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
  return C

def CatmullRomChain(P,alpha):
  """
  Calculate Catmull Rom for a chain of points and return the combined curve.
  """
  sz = len(P)

  # The curve C will contain an array of (x,y) points.
  C = []
  for i in range(sz-3):
    c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3],alpha)
    C.extend(c)

  return C


# In[139]:

# Define a set of points for curve to go through
Points = numpy.random.rand(10,2)
#Points=array([array([153.01,722.67]),array([152.73,699.92]),array([152.91,683.04]),array([154.6,643.45]),
#        array([158.07,603.97])])
#Points = array([array([0,92.05330318]),
#               array([2.39580622,29.76345192]),
#               array([10.01564963,16.91470591]),
#               array([15.26219886,71.56301997]),
#               array([15.51234733,73.76834447]),
#               array([24.88468545,50.89432899]),
#               array([27.83934153,81.1341789]),
#               array([36.80443404,56.55810783]),
#               array([43.1404725,16.96946811]),
#               array([45.27824599,15.75903418]),
#               array([51.58871027,90.63583215])])

x1=Points[0][0]
x2=Points[1][0]
y1=Points[0][1]
y2=Points[1][1]
x3=Points[-2][0]
x4=Points[-1][0]
y3=Points[-2][1]
y4=Points[-1][1]
dom=max(Points[:,0])-min(Points[:,0])
rng=max(Points[:,1])-min(Points[:,1])
pctdom=1
pctdom=float(pctdom)/100
prex=x1+sign(x1-x2)*dom*pctdom
prey=(y1-y2)/(x1-x2)*(prex-x1)+y1
endx=x4+sign(x4-x3)*dom*pctdom
endy=(y4-y3)/(x4-x3)*(endx-x4)+y4
print len(Points)
Points=list(Points)
Points.insert(0,array([prex,prey]))
Points.append(array([endx,endy]))
print len(Points)


# In[140]:

#Define alpha
a=0.

# Calculate the Catmull-Rom splines through the points
c = CatmullRomChain(Points,a)

# Convert the Catmull-Rom curve points into x and y arrays and plot
x,y = zip(*c)
plt.plot(x,y,c='green',zorder=10)

a=0.5
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='blue')

a=1.
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='red')

# Plot the control points
px, py = zip(*Points)
plt.plot(px,py,'o',c='black')

plt.grid(b=True)
plt.show()


# In[141]:

Points


# In[104]:

Paul

I would also note that Catmull Rom is kind of situational for interpolation... since it is not an actual function in the way you might hope for interpolation: It will not give you an f(x), but rather f(t) where t is the distance between two of your points... in linear distance, not x,y distance! Therefore to get simple interpolation you'd have to feed it many "t"s and then maybe linearly interpolate those to get your actual point in x,y space, but you have to be careful you are interpolating along the correct catmull rom segment. – Paul

Answer 3

There's this: jj_catmull, which seems to be in Python, maybe you can find what you need there.

Dharana

ooohhh.. shiny! thanks, I'll take a look at it as soon as possible. It seems like it does what I need, but I need to check in details. – Ima

Nope, it makes strong use of XSi stuff. :( – Ima

This link appears to be dead – Nobby