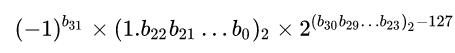Byte representation of float as integer equation

Question

In this article an equation is used I don't understand:

• I = (e + B) * L + m * L

I is the byte representation of a float interpreted as an integer. Here is an example:

float x = 3.5f;
unsigned int i = *((unsigned int *)&x);

• e is the exponent of the float.
• B is the bias (127).
• L is a constant (1 << 23).
• m is the mantissa.

Now my question is:

Why is the equation correct and where can I read more about this equation?

Antineutrino

Answer 1

Floating-Point Encoding

A floating-point number is represented with a sign s, an exponent e, and a significand f. (Some people use the term “mantissa,” but that is a legacy from the days of paper tables of logarithms. “Significand” is preferred for the fraction portion of a floating-point value. Mantissas are logarithmic. Significands are linear.) In binary floating-point, the value represented is + 2^e • f or − 2^e • f, according to the sign s.

Commonly for binary floating-point, the significand is required to be in [1, 2), at least for numbers in the normal range of the format. For encoding, the first bit is separated from the rest, so we may write f = 1 + r, where 0 ≤ r < 1.

In the IEEE 754 basic binary formats, the floating-point number is encoded as a sign bit, some number of exponent bits, and a significand field:

• The sign s is encoded with a 0 bit for positive, 1 for negative. Since we are taking a logarithm, the number is presumably positive, and we may ignore the sign bit for current purposes.

• The exponent bits are the actual exponent plus some bias B. (For 32-bit format, B is 127. For 64-bit, it is 1023.)

• The signifcand field contains the bits of r. Since r is a fraction, the significand field contains the bits of r represented in binary starting after the “binary point.” For example, if r is 5/16, it is “.0101000…” in binary, so the significand field contains 0101000… (For 32-bit format, the significand field contains 23 bits. For 64-bit, 52 bits.)

Let b the number of bits in the significand field (23 or 52). Let L be 2^b.

Then the product of r and L, r • L, is an integer equal to the contents of the significand field. In our example, r is 5/16, L is 2²³ = 8,388,608, and r • L = 2,621,440. So the significand contains 2,621,440, which is 0x280000.

The equation I = (e + B) • L + m • L attempts to capture this. First, the sign is ignored, since it is zero. Then e + B is the exponent plus the bias. Multiplying that by L shifts it left b bits, which puts it in the position of the exponent field of the floating-point encoding. Then adding r • L adds the value of the significand field (for which I use r for “rest of the significand” instead of m for “mantissa”).

Thus, the bits that encode 2^e • (1+r) as a floating-point number are, when interpreted as a binary integer, (e + B) • L + r • L.

More Information

Information about IEEE 754 is in Wikipedia and the IEEE 754 standard. Some previous Stack Overflow answers describing the encoding format at here and here.

Aliasing / Reinterpreting Bits

Regarding the code in your question:

float x = 3.5f;
unsigned int i = *((unsigned int *)&x);

Do not use this code, because its behavior is not defined by the C or C++ standards.

In C, use:

#include <string.h>
...
unsigned int i; memcpy(&i, &x, sizeof i);

or:

unsigned int i = (union { float f; unsigned u; }) { x } .u;

In C++, use:

#include <cstring>
...
unsigned int i; std::memcpy(&i, &x, sizeof i);

These ways are defined to reinterpret the bits of the floating-point encoding as an unsigned int. (Of course, they require that a float and an unsigned int be the same size in the C or C++ implementation you are using.)

Conwell

Answer 2

As you know floating point numbers are stored in IEEE 754 standard. And bit pattern of the single precision floating points like the following (see details here):

And the value of the number is calculated based on the following formula:

Hence, for 32-bit value, the equivalent integer would be e * L + m. Because exponent is started from (23-rd bit) and the first part is m. As supposed the exponent is stored with -127, the expression is transformed to (e + B)*L + m.

About the L after m might be there is an assumption which might not be mentioned in the article.

Moreover, sign bit is not considered in this formula.

Arbe

I don't really see how this does anything more than restate the question. You haven't related e, L, B or m to anything in your picture. – Midkiff