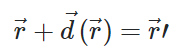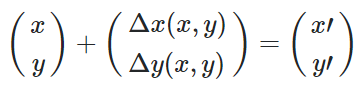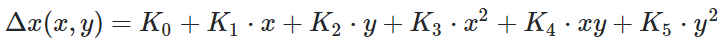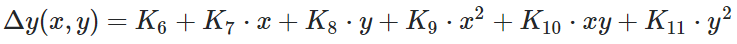Image registration using python and cross-correlation

Question

I got two images showing exaktly the same content: 2D-gaussian-shaped spots. I call these two 16-bit png-files "left.png" and "right.png". But as they are obtained thru an slightly different optical setup, the corresponding spots (physically the same) appear at slightly different positions. Meaning the right is slightly stretched, distorted, or so, in a non-linear way. Therefore I would like to get the transformation from left to right.

So for every pixel on the left side with its x- and y-coordinate I want a function giving me the components of the displacement-vector that points to the corresponding pixel on the right side.

In a former approach I tried to get the positions of the corresponding spots to obtain the relative distances deltaX and deltaY. These distances then I fitted to the taylor-expansion up to second order of T(x,y) giving me the x- and y-component of the displacement vector for every pixel (x,y) on the left, pointing to corresponding pixel (x',y') on the right.

To get a more general result I would like to use normalized cross-correlation. For this I multiply every pixelvalue from left with a corresponding pixelvalue from right and sum over these products. The transformation I am looking for should connect the pixels that will maximize the sum. So when the sum is maximzied, I know that I multiplied the corresponding pixels.

I really tried a lot with this, but didn't manage. My question is if somebody of you has an idea or has ever done something similar.

import numpy as np
import Image

left = np.array(Image.open('left.png'))
right = np.array(Image.open('right.png'))

# for normalization (http://en.wikipedia.org/wiki/Cross-correlation#Normalized_cross-correlation)    
left = (left - left.mean()) / left.std()
right = (right - right.mean()) / right.std()

Please let me know if I can make this question more clear. I still have to check out how to post questions using latex.

Thank you very much for input.

[left.png] https://i.sstatic.net/oSTER.png [right.png] https://i.sstatic.net/Njahj.png

I'm afraid, in most cases 16-bit images appear just black (at least on systems I use) :( but of course there is data in there.

UPDATE 1

I try to clearify my question. I am looking for a vector-field with displacement-vectors that point from every pixel in left.png to the corresponding pixel in right.png. My problem is, that I am not sure about the constraints I have.

where vector r (components x and y) points to a pixel in left.png and vector r-prime (components x-prime and y-prime) points to the corresponding pixel in right.png. for every r there is a displacement-vector.

What I did earlier was, that I found manually components of vector-field d and fitted them to a polynom second degree:

So I fitted:

and

Does this make sense to you? Is it possible to get all the delta-x(x,y) and delta-y(x,y) with cross-correlation? The cross-correlation should be maximized if the corresponding pixels are linked together thru the displacement-vectors, right?

UPDATE 2

So the algorithm I was thinking of is as follows:

1. Deform right.png
2. Get the value of cross-correlation
3. Deform right.png further
4. Get the value of cross-correlation and compare to value before
5. If it's greater, good deformation, if not, redo deformation and do something else
6. After maximzied the cross-correlation value, know what deformation there is :)

About deformation: could one do first a shift along x- and y-direction to maximize cross-correlation, then in a second step stretch or compress x- and y-dependant and in a third step deform quadratic x- and y-dependent and repeat this procedure iterativ?? I really have a problem to do this with integer-coordinates. Do you think I would have to interpolate the picture to obtain a continuous distribution?? I have to think about this again :( Thanks to everybody for taking part :)

Aintab

any help? I'm a little bit stuck on this :( Hope it's not simply ridiculous? – Aintab

How can I make the latex-code interpreted? – Aintab

You can't natively as stackoverflow doesn't support Latex interpretation as math.se does: meta.stackexchange.com/questions/4152/… – Victualer

Thanks Daan. Please look at my Update 2 :) – Aintab

Answer 1

OpenCV (and with it the python Opencv binding) has a StarDetector class which implements this algorithm.

As an alternative you might have a look at the OpenCV SIFT class, which stands for Scale Invariant Feature Transform.

Update

Regarding your comment, I understand that the "right" transformation will maximize the cross-correlation between the images, but I don't understand how you choose the set of transformations over which to maximize. Maybe if you know the coordinates of three matching points (either by some heuristics or by choosing them by hand), and if you expect affinity, you could use something like cv2.getAffineTransform to have a good initial transformation for your maximization process. From there you could use small additional transformations to have a set over which to maximize. But this approach seems to me like re-inventing something which SIFT could take care of.

To actually transform your test image you can use cv2.warpAffine, which also can take care of border values (e.g. pad with 0). To calculate the cross-correlation you could use scipy.signal.correlate2d.

Update

Your latest update did indeed clarify some points for me. But I think that a vector field of displacements is not the most natural thing to look for, and this is also where the misunderstanding came from. I was thinking more along the lines of a global transformation T, which applied to any point (x,y) of the left image gives (x',y')=T(x,y) on the right side, but T has the same analytical form for every pixel. For example, this could be a combination of a displacement, rotation, scaling, maybe some perspective transformation. I cannot say whether it is realistic or not to hope to find such a transformation, this depends on your setup, but if the scene is physically the same on both sides I would say it is reasonable to expect some affine transformation. This is why I suggested cv2.getAffineTransform. It is of course trivial to calculate your displacement Vector field from such a T, as this is just T(x,y)-(x,y).

The big advantage would be that you have only very few degrees of freedom for your transformation, instead of, I would argue, 2N degrees of freedom in the displacement vector field, where N is the number of bright spots.

If it is indeed an affine transformation, I would suggest some algorithm like this:

• identify three bright and well isolated spots on the left
• for each of these three spots, define a bounding box so that you can hope to identify the corresponding spot within it in the right image
• find the coordinates of the corresponding spots, e.g. with some correlation method as implemented in cv2.matchTemplate or by also just finding the brightest spot within the bounding box.
• once you have three matching pairs of coordinates, calculate the affine transformation which transforms one set into the other with cv2.getAffineTransform.
• apply this affine transformation to the left image, as a check if you found the right one you could calculate if the overall normalized cross-correlation is above some threshold or drops significantly if you displace one image with respect to the other.
• if you wish and still need it, calculate the displacement vector field trivially from your transformation T.

Update

It seems cv2.getAffineTransform expects an awkward input data type 'float32'. Let's assume the source coordinates are (sxi,syi) and destination (dxi,dyi) with i=0,1,2, then what you need is

src = np.array( ((sx0,sy0),(sx1,sy1),(sx2,sy2)), dtype='float32' )
dst = np.array( ((dx0,dy0),(dx1,dy1),(dx2,dy2)), dtype='float32' )

result = cv2.getAffineTransform(src,dst)

Paschasia

is there anyone that can provide more input on this? I really would like to know if someone would recommend the cross-correlation to obtain the transformation between the two pictures. – Aintab

I think I still don't understand your initial approach. Could you clarify what T(x,y) is? Around which point do you expand it? – Paschasia

Please look at my Update 1. Do you think I'm on the right way? :) Thank you very much for your answer. – Aintab

do you know how to provide scr and dst in cv2.getAffineTransform(src, dst)? I get error: ..\..\..\OpenCV-2.3.1\modules\imgproc\src\imgwarp.cpp:3201: error: (-215) src.checkVector(2, CV_32F) == 3 && dst.checkVector(2, CV_32F) == 3; I didn't find a userfriendly documentation on this :( – Aintab

An affine transformation probably gives a reasonable approximation of the distortions as they appear to be relatively small. However, they'll never cover all optical distortions which are notably non linear. – Victualer

Correct. This is why I suggested to use the affine transformation as a starting point, and why I also believe that an algorithm based on keypoint detection might get better results. – Paschasia

Thank you very much. The difficulty in keypoint detection to me is, to really put the corresponding spots together and obtain their relative distances. – Aintab

broken link on "this algorithm" (1st link) – Ragsdale

Answer 2

I don't think a cross correlation is going to help here, as it only gives you a single best shift for the whole image. There are three alternatives I would consider:

1. Do a cross correlation on sub-clusters of dots. Take, for example, the three dots in the top right and find the optimal x-y shift through cross-correlation. This gives you the rough transform for the top left. Repeat for as many clusters as you can to obtain a reasonable map of your transformations. Fit this with your Taylor expansion and you might get reasonably close. However, to have your cross-correlation work in any way, the difference in displacement between spots must be less than the extend of the spot, else you can never get all spots in a cluster to overlap simultaneously with a single displacement. Under these conditions, option 2 might be more suitable.

2. If the displacements are relatively small (which I think is a condition for option 1), then we might assume that for a given spot in the left image, the closest spot in the right image is the corresponding spot. Thus, for every spot in the left image, we find the nearest spot in the right image and use that as the displacement in that location. From the 40-something well distributed displacement vectors we can obtain a reasonable approximation of the actual displacement by fitting your Taylor expansion.

3. This is probably the slowest method, but might be the most robust if you have large displacements (and option 2 thus doesn't work): use something like an evolutionary algorithm to find the displacement. Apply a random transformation, compute the remaining error (you might need to define this as sum of the smallest distance between spots in your original and transformed image), and improve your transformation with those results. If your displacements are rather large you might need a very broad search as you'll probably get lots of local minima in your landscape.

I would try option 2 as it seems your displacements might be small enough to easily associate a spot in the left image with a spot in the right image.

Update

I assume your optics induce non linear distortions and having two separate beampaths (different filters in each?) will make the relationship between the two images even more non-linear. The affine transformation PiQuer suggests might give a reasonable approach but can probably never completely cover the actual distortions.

I think your approach of fitting to a low order Taylor polynomial is fine. This works for all my applications with similar conditions. Highest orders probably should be something like xy^2 and x^2y; anything higher than that you won't notice.

Alternatively, you might be able to calibrate the distortions for each image first, and then do your experiments. This way you are not dependent on the distribution of you dots, but can use a high resolution reference image to get the best description of your transformation.

Option 2 above still stands as my suggestion for getting the two images to overlap. This can be fully automated and I'm not sure what you mean when you want a more general result.

Update 2

You comment that you have trouble matching dots in the two images. If this is the case, I think your iterative cross-correlation approach may not be very robust either. You have very small dots, so overlap between them will only occur if the difference between the two images is small.

In principle there is nothing wrong with your proposed solution, but whether it works or not strongly depends on the size of your deformations and the robustness of your optimization algorithm. If you start off with very little overlap, then it may be hard to find a good starting point for your optimization. Yet if you have sufficient overlap to begin with, then you should have been able to find the deformation per dot first, but in a comment you indicate that this doesn't work.

Perhaps you can go for a mixed solution: find the cross correlation of clusters of dots to get a starting point for your optimization, and then tweak the deformation using something like the procedure you describe in your update. Thus:

1. For a NxN pixel segment find the shift between the left and right images
2. Repeat for, say, 16 of those segments
3. Compute an approximation of the deformation using those 16 points
4. Use this as the starting point of your optimization approach

Victualer

You're absolutely right Daan. Thanks for your input. In a former solution I really did find the corresponding maxima on left and right image and took their relative distances in x and y direction to fit on the Tailor expansion to get the displacements for the whole picture. But I thought one could get a more general result with the cross-correlation method. I will think about this problem again and will post my solution for your answers second point. – Aintab

Please look at Update 1 of my question. I'm sorry I don't get the latex-part to work :( Thanks for your answer. – Aintab

That seems like exactly what I would do, using option 2 to automate the process of finding the local shifts. Alternatively, get a calibration test image to compensate for the distortion, and then do your experiments. – Victualer

Thanks for input Daan. The automated solution works fine for my setup with two different pathways/wavelengths. But I would like to calibrate a setup with four different pathways, i.e. four different pictures with distortions. So someone came up with the cross-correlation method, but I don't come to a solution. – Aintab

Answer 3

You might want to have a look at bunwarpj which already does what you're trying to do. It's not python but I use it in exactly this context. You can export a plain text spline transformation and use it if you wish to do so.

Hanny

link not active – Ulda