What you need is to search your cubic path and remember closest point. This can be done recursively with increasing precisions here small C++ GL example:
//---------------------------------------------------------------------------
double pnt[]= // cubic curve control points
{
-0.9,-0.8,0.0,
-0.6,+0.8,0.0,
+0.6,+0.8,0.0,
+0.9,-0.8,0.0,
};
const int pnts3=sizeof(pnt)/sizeof(pnt[0]);
const int pnts=pnts3/3;
//---------------------------------------------------------------------------
double cubic_a[4][3]; // cubic coefficients
void cubic_init(double *pnt) // compute cubic coefficients
{
int i;
double *p0=pnt,*p1=p0+3,*p2=p1+3,*p3=p2+3;
for (i=0;i<3;i++) // cubic BEZIER coefficients
{
cubic_a[0][i]= ( p0[i]);
cubic_a[1][i]= (3.0*p1[i])-(3.0*p0[i]);
cubic_a[2][i]= (3.0*p2[i])-(6.0*p1[i])+(3.0*p0[i]);
cubic_a[3][i]=( p3[i])-(3.0*p2[i])+(3.0*p1[i])-( p0[i]);
}
}
//---------------------------------------------------------------------------
double* cubic(double t) // return point on cubic from parameter
{
int i;
static double p[3];
double tt=t*t,ttt=tt*t;
for (i=0;i<3;i++)
p[i]=cubic_a[0][i]
+(cubic_a[1][i]*t)
+(cubic_a[2][i]*tt)
+(cubic_a[3][i]*ttt);
return p;
}
//---------------------------------------------------------------------------
double cubic_d(double *p) // return closest distance from point to cubic
{
int i,j;
double t,tt,t0,t1,dt,
l,ll,a,*q;
tt=-1.0; ll=-1.0; t0=0.0; t1=1.001; dt=0.05;
for (j=0;j<3;j++)
{
for (t=t0;t<=t1;t+=dt)
{
q=cubic(t);
for (l=0.0,i=0;i<3;i++) l+=(p[i]-q[i])*(p[i]-q[i]);
if ((ll<0.0)||(ll>l)){ ll=l; tt=t; }
}
t0=tt-dt; if (t0<0.0) t0=0.0;
t1=tt+dt; if (t1>1.0) t1=1.0;
dt*=0.2;
}
return sqrt(ll);
}
//---------------------------------------------------------------------------
void gl_draw()
{
int i;
double t,p[3],dp;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnable(GL_CULL_FACE);
// GL render
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glDisable(GL_DEPTH_TEST);
glColor3f(0.2,0.2,0.2); glBegin(GL_LINE_STRIP); for (i=0;i<pnts3;i+=3) glVertex3dv(pnt+i); glEnd();
glPointSize(5); glColor3f(0.0,0.0,0.7); glBegin(GL_POINTS); for (i=0;i<pnts3;i+=3) glVertex3dv(pnt+i); glEnd(); glPointSize(1);
cubic_init(pnt);glColor3f(0.2,0.7,0.7); glBegin(GL_LINE_STRIP); for (t=0.0;t<1.001;t+=0.025) glVertex3dv(cubic(t)); glEnd();
glColor3f(0.0,0.7,0.0); glBegin(GL_POINTS);
p[2]=0.0; dp=0.01;
for (p[0]=-1.0;p[0]<1.001;p[0]+=dp)
for (p[1]=-1.0;p[1]<1.001;p[1]+=dp)
if (cubic_d(p)<0.05)
glVertex3dv(p);
glEnd();
glFlush();
SwapBuffers(hdc);
}
//---------------------------------------------------------------------------
so first you call cubic_init once to compute the coefficients and then to obtain point on curve as function of parameter use:
double pnt[3] = cubic(double t);
Now the reverse (I return closest distance ll but you can easily change it to return the tt)
double dist = cubic_d(double pnt[3]);
Now you just port this to shader and determine if fragment is close enough to curve to render it (hence the distance instead of t also for speed you can get rid of the last sqrt and use powered values latter).
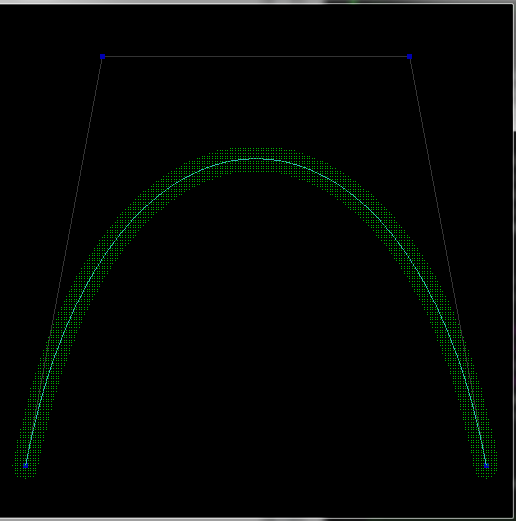
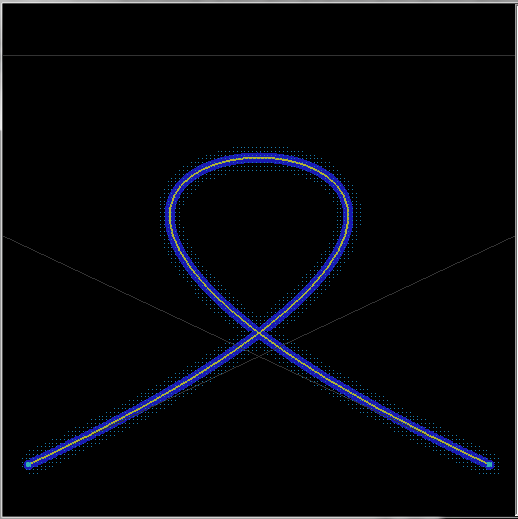
The gl_draw function renders control points(blue) / lines(gray) the bezier curve (aqua) with GL and then emulates fragment shader to render curve with thickness 2*0.05 in (green)...
Preview:
![preview]()
Now its just a matter of porting that into GLSL. In order to use GLSL native way of passing vertexes you need to enlarge the area a bit like in here:
But you need to change the geometry a bit to account for 4 control points instead of just 3. That stuff should be in geometry shader ...
So in geometry shader you should do the cubic_init, and in fragment shader discard if distance cubic_d is bigger than thickness.
The search is based on:
which I develop for problems like this. The search loop itself can be tweaked a bit to improve performance/precision ... but beware the initial search should sample the curve to at least 4-5 chunks otherwise it might stop working properly for some shapes.
[Edit1] after some thinking here the GLSL version
Vertex
// Vertex
#version 400 core
layout(location = 0) in vec2 pos; // control points (QUADS)
layout(location = 3) in vec3 col; // color
out vec2 vpos;
out vec3 vcol;
void main()
{
vpos=pos;
vcol=col;
gl_Position=vec4(pos,0.0,1.0);
}
Geometry:
//------------------------------------------------------------------------------
// Geometry
//------------------------------------------------------------------------------
#version 400 core
layout(lines_adjacency) in;
layout(triangle_strip, max_vertices = 4) out;
uniform float d=0.05; // half thickness
in vec2 vpos[];
in vec3 vcol[];
out vec2 a0,a1,a2,a3; // cubic coefficients
out vec3 fcol; // color
out vec2 fpos; // position
//------------------------------------------------------------------------------
void main()
{
vec4 p0,p1,p2,p3,a,b;
p0=gl_in[0].gl_Position;
p1=gl_in[1].gl_Position;
p2=gl_in[2].gl_Position;
p3=gl_in[3].gl_Position;
// compute BEZIER coefficients
a0.x= ( p0.x);
a1.x= (3.0*p1.x)-(3.0*p0.x);
a2.x= (3.0*p2.x)-(6.0*p1.x)+(3.0*p0.x);
a3.x=(p3.x)-(3.0*p2.x)+(3.0*p1.x)-( p0.x);
a0.y= ( p0.y);
a1.y= (3.0*p1.y)-(3.0*p0.y);
a2.y= (3.0*p2.y)-(6.0*p1.y)+(3.0*p0.y);
a3.y=(p3.y)-(3.0*p2.y)+(3.0*p1.y)-( p0.y);
// compute BBOX
a=p0; b=p0;
if (a.x > p1.x) a.x=p1.x; if (b.x < p1.x) b.x=p1.x;
if (a.x > p2.x) a.x=p2.x; if (b.x < p2.x) b.x=p2.x;
if (a.x > p3.x) a.x=p3.x; if (b.x < p3.x) b.x=p3.x;
if (a.y > p1.y) a.y=p1.y; if (b.y < p1.y) b.y=p1.y;
if (a.y > p2.y) a.y=p2.y; if (b.y < p2.y) b.y=p2.y;
if (a.y > p3.y) a.y=p3.y; if (b.y < p3.y) b.y=p3.y;
// enlarge by d
a.x-=d; a.y-=d;
b.x+=d; b.y+=d;
// pass it as QUAD
fcol=vcol[0];
fpos=vec2(a.x,a.y); gl_Position=vec4(a.x,a.y,0.0,1.0); EmitVertex();
fpos=vec2(a.x,b.y); gl_Position=vec4(a.x,b.y,0.0,1.0); EmitVertex();
fpos=vec2(b.x,a.y); gl_Position=vec4(b.x,a.y,0.0,1.0); EmitVertex();
fpos=vec2(b.x,b.y); gl_Position=vec4(b.x,b.y,0.0,1.0); EmitVertex();
EndPrimitive();
}
//------------------------------------------------------------------------------
Fragment:
// Fragment
#version 400 core
uniform float d=0.05; // half thickness
in vec2 fpos; // fragment position
in vec3 fcol; // fragment color
in vec2 a0,a1,a2,a3; // cubic coefficients
out vec4 col;
vec2 cubic(float t) // return point on cubic from parameter
{
float tt=t*t,ttt=tt*t;
return a0+(a1*t)+(a2*tt)+(a3*ttt);
}
void main()
{
vec2 p;
int i;
float t,tt,t0,t1,dt,l,ll;
tt=-1.0; ll=-1.0; dt=0.05; t0=0.0; t1=1.0; l=0.0;
for (i=0;i<3;i++)
{
for (t=t0;t<=t1;t+=dt)
{
p=cubic(t)-fpos;
l=length(p);
if ((ll<0.0)||(ll>l)){ ll=l; tt=t; }
}
t0=tt-dt; if (t0<0.0) t0=0.0;
t1=tt+dt; if (t1>1.0) t1=1.0;
dt*=0.2;
}
if (ll>d) discard;
col=vec4(fcol,1.0); // ll,tt can be used for coloring or texturing
}
It expect 4 BEZIER control points per CUBIC in form of GL_LINES_ADJACENCY since GL_QUADS are no more :( When I use it like this (inside gl_draw):
glUseProgram(prog_id); // use our shaders
i=glGetUniformLocation(prog_id,"d"); // set line half thickness
glUniform1f(i,0.02);
glColor3f(0.2,0.7,0.2); // color
glBegin(GL_LINES_ADJACENCY);
for (i=0;i<pnts3;i+=3)
glVertex3dv(pnt+i);
glEnd();
glUseProgram(0);
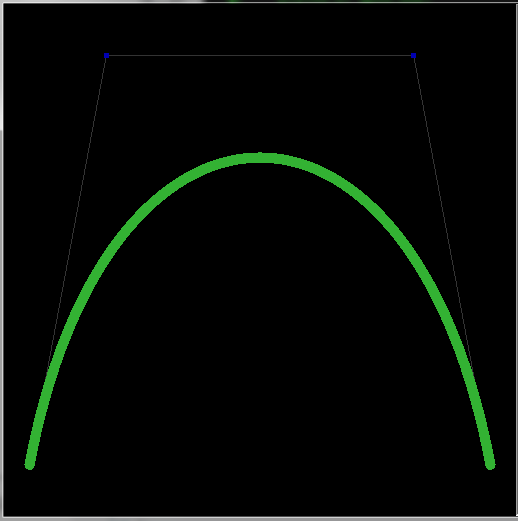
The result looks like this:
![shader preview]()
and of coarse is a lot of faster than the old api dotted shader emulation :). I know old api and new style GLSL shaders should not be mixed so you should create VAO/VBO instead of using glBegin/glEnd... I am too lazy to do that just for the purpose of this answer ...
Here the non function (more y per single x) example (compared with the CPU side dots):
double pnt[]= // cubic curve control points
{
+0.9,-0.8,0.0,
-2.5,+0.8,0.0,
+2.5,+0.8,0.0,
-0.9,-0.8,0.0,
};
![non function]()
As you can see both approaches matches the shape (dots used bigger thickness). In order this to work the search coefficients (dt) must be set properly to not miss a solution...
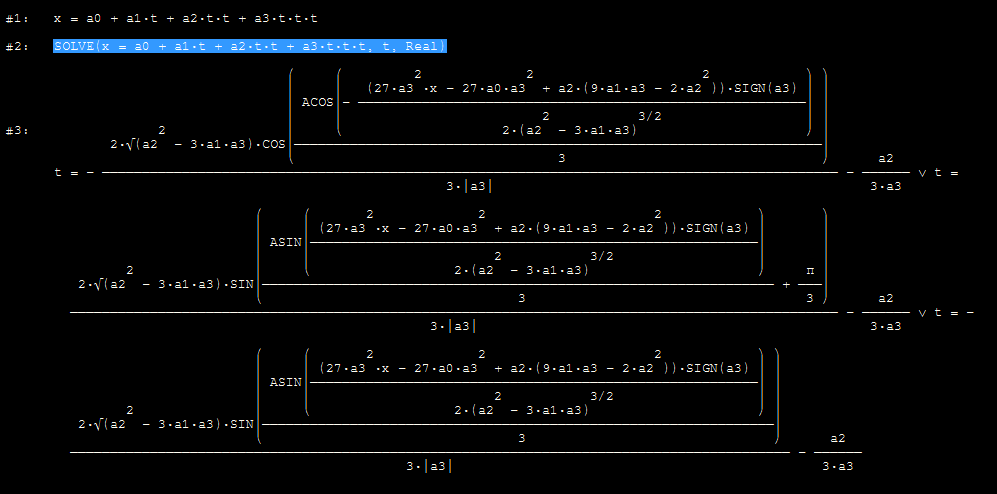
PS solving the cubic your way leads to 2 set of these:
![analytical solution]()
Which I strongly doubt can be much computed faster than simple search.
[Edit2] further improvements
I simply changed the geometry shader so that it sample the curve into 10 segments and emit BBOX for each separatelly eliminating a lot of empty space that needed to be processed before. I changed the color layout and rendering order a bit.
This is new result (identical to previous one but several times faster due lower empty space ratio):
![preview]()
This is how the coverage looks now:
![coverage]()
Before the coverage was BBOX of control points + enlargement by d which in this case was much bigger then curve itself (2 control points are outside view).
Here updated Geometry shader:
//------------------------------------------------------------------------------
// Geometry
//------------------------------------------------------------------------------
#version 400 core
layout(lines_adjacency) in;
layout(triangle_strip, max_vertices = 40) out; // 4*n <= 60
uniform float d=0.05; // half thickness
in vec2 vpos[];
in vec3 vcol[];
out vec2 a0,a1,a2,a3; // cubic coefficients
out vec3 fcol; // color
out vec2 fpos; // position
//------------------------------------------------------------------------------
vec2 cubic(float t) // return point on cubic from parameter
{
float tt=t*t,ttt=tt*t;
return a0+(a1*t)+(a2*tt)+(a3*ttt);
}
//------------------------------------------------------------------------------
void main()
{
float t,dt=1.0/10.0; // 1/n
vec2 p0,p1,p2,p3,a,b;
p0=gl_in[0].gl_Position.xy;
p1=gl_in[1].gl_Position.xy;
p2=gl_in[2].gl_Position.xy;
p3=gl_in[3].gl_Position.xy;
// compute BEZIER coefficients
a0.x= ( p0.x);
a1.x= (3.0*p1.x)-(3.0*p0.x);
a2.x= (3.0*p2.x)-(6.0*p1.x)+(3.0*p0.x);
a3.x=(p3.x)-(3.0*p2.x)+(3.0*p1.x)-( p0.x);
a0.y= ( p0.y);
a1.y= (3.0*p1.y)-(3.0*p0.y);
a2.y= (3.0*p2.y)-(6.0*p1.y)+(3.0*p0.y);
a3.y=(p3.y)-(3.0*p2.y)+(3.0*p1.y)-( p0.y);
p1=cubic(0.0);
for (t=dt;t < 1.001;t+=dt)
{
p0=p1; p1=cubic(t);
// compute BBOX
a=p0; b=p0;
if (a.x > p1.x) a.x=p1.x; if (b.x < p1.x) b.x=p1.x;
if (a.y > p1.y) a.y=p1.y; if (b.y < p1.y) b.y=p1.y;
// enlarge by d
a.x-=d; a.y-=d;
b.x+=d; b.y+=d;
// pass it as QUAD
fcol=vcol[0];
fpos=vec2(a.x,a.y); gl_Position=vec4(a.x,a.y,0.0,1.0); EmitVertex();
fpos=vec2(a.x,b.y); gl_Position=vec4(a.x,b.y,0.0,1.0); EmitVertex();
fpos=vec2(b.x,a.y); gl_Position=vec4(b.x,a.y,0.0,1.0); EmitVertex();
fpos=vec2(b.x,b.y); gl_Position=vec4(b.x,b.y,0.0,1.0); EmitVertex();
EndPrimitive();
}
}
//------------------------------------------------------------------------------
My gfx card has 60 vertex limit so as I output triangle strips emulating QUADs the limit on segments is 60/4 = 15 I used n=10 just to be sure it runs on lower HW. In order to change the number of segments see the 2 lines with comment containing n
[Edit3] even better coverage useful/empty space ratio
I changed the AABB BBOX coverage to ~OOB BBOX without overlaps. This also allows to pass actual range of t into fragment speeding up the search ~10 times. Updated shaders:
Vertex:
// Vertex
#version 400 core
layout(location = 0) in vec2 pos; // control points (QUADS)
layout(location = 3) in vec3 col; // color
out vec2 vpos;
out vec3 vcol;
void main()
{
vpos=pos;
vcol=col;
gl_Position=vec4(pos,0.0,1.0);
}
Geometry:
//------------------------------------------------------------------------------
// Geometry
//------------------------------------------------------------------------------
#version 400 core
layout(lines_adjacency) in;
layout(triangle_strip, max_vertices = 40) out; // 4*n <= 60
uniform float d=0.05; // half thickness
in vec2 vpos[];
in vec3 vcol[];
out vec2 a0,a1,a2,a3; // cubic coefficients
out vec3 fcol; // color
out vec2 fpos; // position
out vec2 trange; // t range of chunk
//------------------------------------------------------------------------------
vec2 cubic(float t) // return point on cubic from parameter
{
float tt=t*t,ttt=tt*t;
return a0+(a1*t)+(a2*tt)+(a3*ttt);
}
//------------------------------------------------------------------------------
void main()
{
int i,j,n=10,m=10; // n,m
float t,dd,d0,d1,dt=1.0/10.0; // 1/n
float tt,dtt=1.0/100.0; // 1/(n*m)
vec2 p0,p1,p2,p3,u,v;
vec2 q0,q1,q2,q3;
p0=gl_in[0].gl_Position.xy;
p1=gl_in[1].gl_Position.xy;
p2=gl_in[2].gl_Position.xy;
p3=gl_in[3].gl_Position.xy;
// compute BEZIER coefficients
a0.x= ( p0.x);
a1.x= (3.0*p1.x)-(3.0*p0.x);
a2.x= (3.0*p2.x)-(6.0*p1.x)+(3.0*p0.x);
a3.x=(p3.x)-(3.0*p2.x)+(3.0*p1.x)-( p0.x);
a0.y= ( p0.y);
a1.y= (3.0*p1.y)-(3.0*p0.y);
a2.y= (3.0*p2.y)-(6.0*p1.y)+(3.0*p0.y);
a3.y=(p3.y)-(3.0*p2.y)+(3.0*p1.y)-( p0.y);
q2=vec2(0.0,0.0);
q3=vec2(0.0,0.0);
// sample curve by chunks
for (p1=cubic(0.0),i=0,t=dt;i<n;i++,t+=dt)
{
// sample point
p0=p1; p1=cubic(t); q0=q2; q1=q3;
// compute ~OBB enlarged by D
u=normalize(p1-p0);
v=vec2(u.y,-u.x);
// resample chunk to compute enlargement
for (d0=0.0,d1=0.0,tt=t-dtt,j=2;j<m;j++,tt-=dtt)
{
dd=dot(cubic(tt)-p0,v);
d0=max(-dd,d0);
d1=max(+dd,d1);
}
d0+=d; d1+=d; u*=d;
d0*=1.25; d1*=1.25; // just to be sure
// enlarge radial
q2=p1+(v*d1);
q3=p1-(v*d0);
// enlarge axial
if (i==0)
{
q0=p0+(v*d1)-u;
q1=p0-(v*d0)-u;
}
if (i==n-1)
{
q2+=u;
q3+=u;
}
// pass it as QUAD
fcol=vcol[0]; trange=vec2(t-dt,t);
fpos=q0; gl_Position=vec4(q0,0.0,1.0); EmitVertex();
fpos=q1; gl_Position=vec4(q1,0.0,1.0); EmitVertex();
fpos=q2; gl_Position=vec4(q2,0.0,1.0); EmitVertex();
fpos=q3; gl_Position=vec4(q3,0.0,1.0); EmitVertex();
EndPrimitive();
}
}
//------------------------------------------------------------------------------*
Fragment:
// Fragment
#version 400 core
//#define show_coverage
uniform float d=0.05; // half thickness
in vec2 fpos; // fragment position
in vec3 fcol; // fragment color
in vec2 a0,a1,a2,a3; // cubic coefficients
in vec2 trange; // t range of chunk
out vec4 col;
vec2 cubic(float t) // return point on cubic from parameter
{
float tt=t*t,ttt=tt*t;
return a0+(a1*t)+(a2*tt)+(a3*ttt);
}
void main()
{
vec2 p;
int i,n;
float t,tt,t0,t1,dt,l,ll;
tt=-1.0; ll=-1.0; l=0.0;
#ifdef show_coverage
t0=0.0; t1=1.0; dt=0.05; n=3;
#else
t0=trange.x; n=2;
t1=trange.y;
dt=(t1-t0)*0.1;
#endif
for (i=0;i<n;i++)
{
for (t=t0;t<=t1;t+=dt)
{
p=cubic(t)-fpos;
l=length(p);
if ((ll<0.0)||(ll>l)){ ll=l; tt=t; }
}
t0=tt-dt; if (t0<0.0) t0=0.0;
t1=tt+dt; if (t1>1.0) t1=1.0;
dt*=0.2;
}
#ifdef show_coverage
if (ll>d) col=vec4(0.1,0.1,0.1,1.0); else
#else
if (ll>d) discard;
#endif
col=vec4(fcol,1.0);
}
And preview (curve + coverage):
![better coverage]()
And just curve:
![curve]()
as You can see the seam at the crossing wit hcoverage is due to coverage rendering without blending. The curve itself is OK.
The d0,d1 parameters are the max perpendicular distances to th actual chunk OBB axial axis (u) enlarged by d and scaled up by 25% just to be sure. Looks like it fits very good. I doubt there is much to be gained by further optimizations as this result is pretty close to perfect fit of the coverage...
the #define show_coverage just enables to view what geometry is passed to fragment shader ...





tyou need to find perpendicular distance to curve ... it might be done by approximation or bisection search but you will not avoidforloop ... – Prod