Why is numpy's einsum faster than numpy's built in functions?

Question

Lets start with three arrays of dtype=np.double. Timings are performed on a intel CPU using numpy 1.7.1 compiled with icc and linked to intel's mkl. A AMD cpu with numpy 1.6.1 compiled with gcc without mkl was also used to verify the timings. Please note the timings scale nearly linearly with system size and are not due to the small overhead incurred in the numpy functions if statements these difference will show up in microseconds not milliseconds:

arr_1D=np.arange(500,dtype=np.double)
large_arr_1D=np.arange(100000,dtype=np.double)
arr_2D=np.arange(500**2,dtype=np.double).reshape(500,500)
arr_3D=np.arange(500**3,dtype=np.double).reshape(500,500,500)

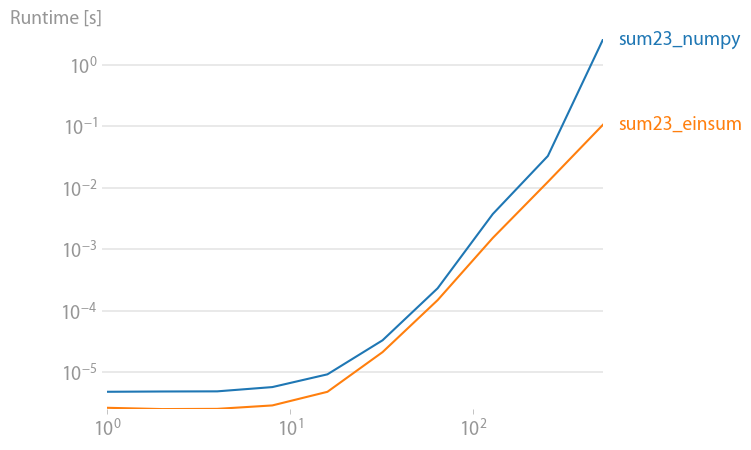
First lets look at the np.sum function:

np.all(np.sum(arr_3D)==np.einsum('ijk->',arr_3D))
True

%timeit np.sum(arr_3D)
10 loops, best of 3: 142 ms per loop

%timeit np.einsum('ijk->', arr_3D)
10 loops, best of 3: 70.2 ms per loop

Powers:

np.allclose(arr_3D*arr_3D*arr_3D,np.einsum('ijk,ijk,ijk->ijk',arr_3D,arr_3D,arr_3D))
True

%timeit arr_3D*arr_3D*arr_3D
1 loops, best of 3: 1.32 s per loop

%timeit np.einsum('ijk,ijk,ijk->ijk', arr_3D, arr_3D, arr_3D)
1 loops, best of 3: 694 ms per loop

Outer product:

np.all(np.outer(arr_1D,arr_1D)==np.einsum('i,k->ik',arr_1D,arr_1D))
True

%timeit np.outer(arr_1D, arr_1D)
1000 loops, best of 3: 411 us per loop

%timeit np.einsum('i,k->ik', arr_1D, arr_1D)
1000 loops, best of 3: 245 us per loop

All of the above are twice as fast with np.einsum. These should be apples to apples comparisons as everything is specifically of dtype=np.double. I would expect the speed up in an operation like this:

np.allclose(np.sum(arr_2D*arr_3D),np.einsum('ij,oij->',arr_2D,arr_3D))
True

%timeit np.sum(arr_2D*arr_3D)
1 loops, best of 3: 813 ms per loop

%timeit np.einsum('ij,oij->', arr_2D, arr_3D)
10 loops, best of 3: 85.1 ms per loop

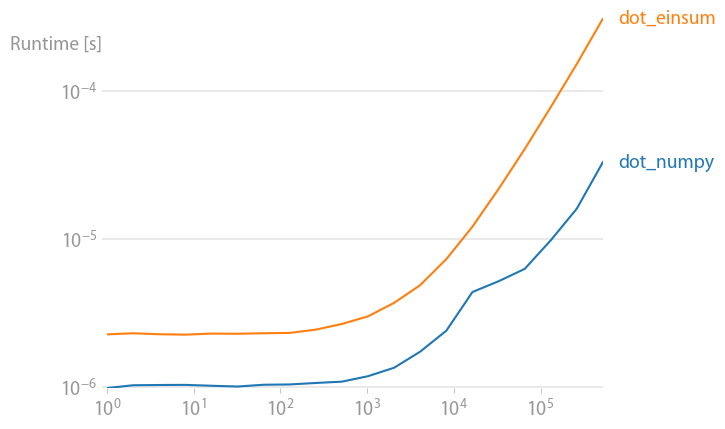
Einsum seems to be at least twice as fast for np.inner, np.outer, np.kron, and np.sum regardless of axes selection. The primary exception being np.dot as it calls DGEMM from a BLAS library. So why is np.einsum faster that other numpy functions that are equivalent?

The DGEMM case for completeness:

np.allclose(np.dot(arr_2D,arr_2D),np.einsum('ij,jk',arr_2D,arr_2D))
True

%timeit np.einsum('ij,jk',arr_2D,arr_2D)
10 loops, best of 3: 56.1 ms per loop

%timeit np.dot(arr_2D,arr_2D)
100 loops, best of 3: 5.17 ms per loop

---

The leading theory is from @sebergs comment that np.einsum can make use of SSE2, but numpy's ufuncs will not until numpy 1.8 (see the change log). I believe this is the correct answer, but have not been able to confirm it. Some limited proof can be found by changing the dtype of input array and observing speed difference and the fact that not everyone observes the same trends in timings.

Scour

What BLAS library is numpy linked against? Is it multithreaded? – Basilbasilar

Multithreaded MKL BLAS with AVX. – Scour

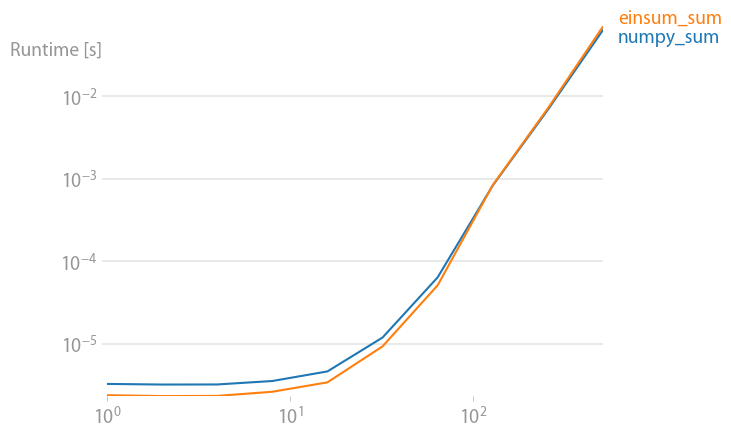
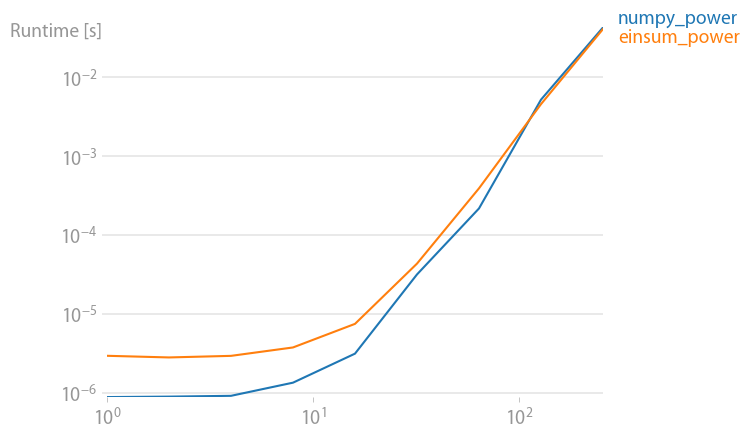
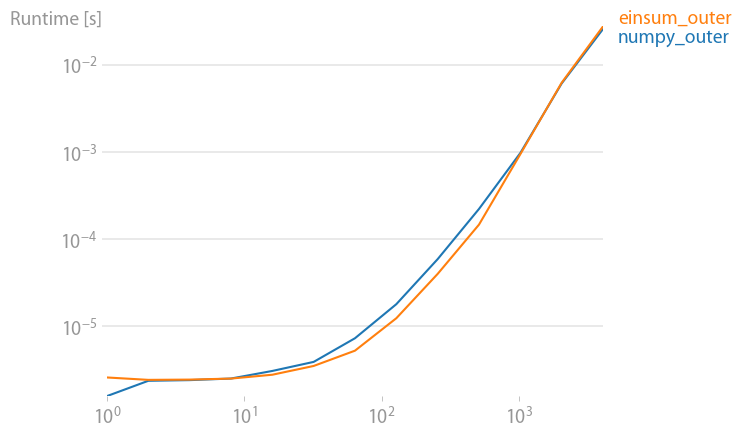
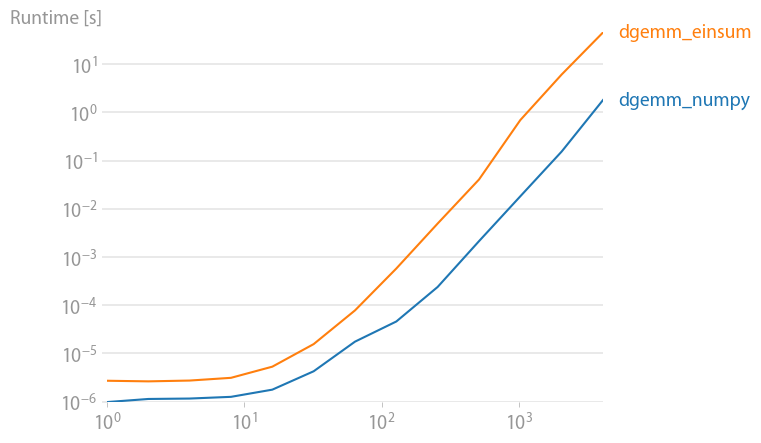
Incidentally, great question, and good examples! It might be worth asking this on the mailing list. It's been covered before (particularly with regards to sum), but I'm surprised that einsum is consistently ~2x faster than outer, inner, kron, etc. It would be interesting to know where the difference come from. – Screamer

@JoeKington I think I will post it on the mailing list if someone else can reproduce the ~2x speedup. Strangely Jamie's answer does demonstrate this. – Scour

somewhat related: #17527840 but in that case, the reason for differences in speed seems to be memory management, (when you start making stuff really big at least) – Hyperbaton

@Hyperbaton Good point; however, definitely not memory issues here. – Scour

@Ophion i guess the fastest way would be with pycuda if you really want to push it to big sizes? though i do not really have experience with it, i would be interested to hear what others have tested out – Hyperbaton

@Hyperbaton This question is not really about how to execute the code the fastest. A cython/numba/f2py implementation would probably be the way to go if you are really worried about speed. This question is focusing on the why of it. np.sum should be equally as fast, if not faster, then np.einsum (of course ignoring the 3-30 us penalty that Jaime showed), but its not. – Scour

2019 update: Numpy's native functions are now faster than einsums in almost all cases. (See my answer for details.) – Orna

Thanks @NicoSchlömer for the new benchmarks. It appears that this is now true for binary operations, but does not hold up for any operation where einsum can elide canonical intermediates (most operations that are not binary). A blanket statement here is a bit dangerous. – Scour

Answer 1

Now that numpy 1.8 is released, where according to the docs all ufuncs should use SSE2, I wanted to double check that Seberg's comment about SSE2 was valid.

To perform the test a new python 2.7 install was created- numpy 1.7 and 1.8 were compiled with icc using standard options on a AMD opteron core running Ubuntu.

This is the test run both before and after the 1.8 upgrade:

import numpy as np
import timeit

arr_1D=np.arange(5000,dtype=np.double)
arr_2D=np.arange(500**2,dtype=np.double).reshape(500,500)
arr_3D=np.arange(500**3,dtype=np.double).reshape(500,500,500)

print 'Summation test:'
print timeit.timeit('np.sum(arr_3D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print timeit.timeit('np.einsum("ijk->", arr_3D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print '----------------------\n'


print 'Power test:'
print timeit.timeit('arr_3D*arr_3D*arr_3D',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print timeit.timeit('np.einsum("ijk,ijk,ijk->ijk", arr_3D, arr_3D, arr_3D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print '----------------------\n'


print 'Outer test:'
print timeit.timeit('np.outer(arr_1D, arr_1D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print timeit.timeit('np.einsum("i,k->ik", arr_1D, arr_1D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print '----------------------\n'


print 'Einsum test:'
print timeit.timeit('np.sum(arr_2D*arr_3D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print timeit.timeit('np.einsum("ij,oij->", arr_2D, arr_3D)',
                      'import numpy as np; from __main__ import arr_1D, arr_2D, arr_3D',
                      number=5)/5
print '----------------------\n'

Numpy 1.7.1:

Summation test:
0.172988510132
0.0934836149216
----------------------

Power test:
1.93524689674
0.839519000053
----------------------

Outer test:
0.130380821228
0.121401786804
----------------------

Einsum test:
0.979052495956
0.126066613197

Numpy 1.8:

Summation test:
0.116551589966
0.0920487880707
----------------------

Power test:
1.23683619499
0.815982818604
----------------------

Outer test:
0.131808176041
0.127472200394
----------------------

Einsum test:
0.781750011444
0.129271841049

I think this is fairly conclusive that SSE plays a large role in the timing differences, it should be noted that repeating these tests the timings very by only ~0.003s. The remaining difference should be covered in the other answers to this question.

Scour

Fantastic followup! This is one more reason why I need to start using einsum more often. Incidentally, I'd argue you should really mark your own answer as correct, in this case. – Screamer

Answer 2

First off, there's been a lot of past discussion about this on the numpy list. For example, see:

• https://mail.python.org/archives/list/[email protected]/thread/MYB7HYCIZIQSFYIUEJU33RBESP5GNJPP/#MYB7HYCIZIQSFYIUEJU33RBESP5GNJPP
• https://mail.python.org/archives/list/[email protected]/thread/LKHZ4NCDALIIMLAOXPK4GL55JHSLINXK/#LKHZ4NCDALIIMLAOXPK4GL55JHSLINXK

Some of boils down to the fact that einsum is new, and is presumably trying to be better about cache alignment and other memory access issues, while many of the older numpy functions focus on a easily portable implementation over a heavily optimized one. I'm just speculating, there, though.

---

However, some of what you're doing isn't quite an "apples-to-apples" comparison.

In addition to what @Jamie already said, sum uses a more appropriate accumulator for arrays

For example, sum is more careful about checking the type of the input and using an appropriate accumulator. For example, consider the following:

In [1]: x = 255 * np.ones(100, dtype=np.uint8)

In [2]: x
Out[2]:
array([255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255,
       255, 255, 255, 255, 255, 255, 255, 255, 255], dtype=uint8)

Note that the sum is correct:

In [3]: x.sum()
Out[3]: 25500

While einsum will give the wrong result:

In [4]: np.einsum('i->', x)
Out[4]: 156

But if we use a less limited dtype, we'll still get the result you'd expect:

In [5]: y = 255 * np.ones(100)

In [6]: np.einsum('i->', y)
Out[6]: 25500.0

Screamer

Do you have a good link for how sum picks the accumulator? Interestingly with your x array extend to 1E8 elements np.einsum('i->',x,dtype=np.uint64) is only about 10% faster (15ms) then sum. – Scour

@Ophion - The documentation for sum has some details. You can specify it with the dtype kwarg to sum. If it's not specified, and the array has an integer dtype with less precision than the "default platform integer" (usually int64 even on 32-bit platforms, I think), then it defaults to the default integer. See: docs.scipy.org/doc/numpy/reference/generated/numpy.sum.html – Screamer

Also, sum is implemented through np.add.reduce, so have a look at the source for reduction ufuncs here, if you're interested in the details: github.com/numpy/numpy/blob/master/numpy/core/src/umath/… – Screamer

If I understand it correctly, these are 'apples-to-apples' comparisons as everything is specifically confined to dtype=np.double? – Scour

I think so. Which is what you were doing in the first place, after all. Therefore, the point I brought up probably isn't that relevant after all! – Screamer

Answer 3

I think these timings explain what's going on:

a = np.arange(1000, dtype=np.double)
%timeit np.einsum('i->', a)
100000 loops, best of 3: 3.32 us per loop
%timeit np.sum(a)
100000 loops, best of 3: 6.84 us per loop

a = np.arange(10000, dtype=np.double)
%timeit np.einsum('i->', a)
100000 loops, best of 3: 12.6 us per loop
%timeit np.sum(a)
100000 loops, best of 3: 16.5 us per loop

a = np.arange(100000, dtype=np.double)
%timeit np.einsum('i->', a)
10000 loops, best of 3: 103 us per loop
%timeit np.sum(a)
10000 loops, best of 3: 109 us per loop

So you basically have an almost constant 3us overhead when calling np.sum over np.einsum, so they basically run as fast, but one takes a little longer to get going. Why could that be? My money is on the following:

a = np.arange(1000, dtype=object)
%timeit np.einsum('i->', a)
Traceback (most recent call last):
...
TypeError: invalid data type for einsum
%timeit np.sum(a)
10000 loops, best of 3: 20.3 us per loop

Not sure what is going on exactly, but it seems that np.einsum is skipping some checks to extract type specific functions to do the multiplications and additions, and is going directly with * and + for standard C types only.

---

The multidimensional cases are not different:

n = 10; a = np.arange(n**3, dtype=np.double).reshape(n, n, n)
%timeit np.einsum('ijk->', a)
100000 loops, best of 3: 3.79 us per loop
%timeit np.sum(a)
100000 loops, best of 3: 7.33 us per loop

n = 100; a = np.arange(n**3, dtype=np.double).reshape(n, n, n)
%timeit np.einsum('ijk->', a)
1000 loops, best of 3: 1.2 ms per loop
%timeit np.sum(a)
1000 loops, best of 3: 1.23 ms per loop

So a mostly constant overhead, not a faster running once they get down to it.

Wolfie

Also, the documentation suggests that einsum does not perform automatic broadcasting either, and relies on the user to express the broadcasting rules for an operation. So there are probably a lot of checks (type checking, broadcasting, etc.) that einsum is able to skip. – Wolves

Strangely they are different on my machine, please view my edit. – Scour

1 or more dimensions is basically the same thing. np.sum calls np.add.reduce, and that was redone for 1.7 to accept multiple axes. So the iteration is almost certainly being handled by a very similar call to the C equivalent of np.nditer in both cases. Unless you are avoiding intermediate arrays to do the multiply-then-add thing that numpy does, or you are using a multi-threaded library, you should see little differences apart from set up, which is what my timings kind of show. – Wolfie

I was trying to point out my timings, in numpy 1.7.1 are very different then these, on my machine your last example is 540us (einsum) and 1.18ms (sum). The timing differences I have shown are not on the order of microseconds, but in some cases milliseconds. – Scour

Incidentally I can reproduce the 2X speedup with einsum on a AMD cpu, without mkl linked and numpy 1.6.1. Does anyone else see the same timing trends that I do? – Scour

You should probably see a 2x speedup with double precision (SSE). Because sum is naive (might not be on 1.8+ not sure), while einsum is specifically written to use of SIMD instructions, most of the ufuncs do not. – Battology

@Battology You nailed it, both processors have SSE2 so one would expect single precision to be 4x as fast and it is. If you can write this up I will accept it. – Scour

I have results similar to @Ophion rather than Jaime, I have a 2x speedup too. Also my proc have SSE. – Nettles

@Wolfie Can you confirm your CPU does not support SSE2 or your numpy version was compiled the nosse flag? – Scour

My CPU does support SSE2, at least according to Wikipedia: it's an Intel Core i5. As for my numpy, I got it bundled in WinPython, not sure how it was compiled... – Wolfie

Answer 4

An update for numpy 1.21.2: Numpy's native functions are faster than einsums in almost all cases. Only einsum's outer variant and the sum23 test faster than the non-einsum versions.

If you can use numpy's native functions, do that.

(Images created with perfplot, a project of mine.)

---

Code to reproduce the plots:

import numpy
import perfplot


def setup1(n):
    return numpy.arange(n, dtype=numpy.double)


def setup2(n):
    return numpy.arange(n ** 2, dtype=numpy.double).reshape(n, n)


def setup3(n):
    return numpy.arange(n ** 3, dtype=numpy.double).reshape(n, n, n)


def setup23(n):
    return (
        numpy.arange(n ** 2, dtype=numpy.double).reshape(n, n),
        numpy.arange(n ** 3, dtype=numpy.double).reshape(n, n, n),
    )


def numpy_sum(a):
    return numpy.sum(a)


def einsum_sum(a):
    return numpy.einsum("ijk->", a)


perfplot.save(
    "sum.png",
    setup=setup3,
    kernels=[numpy_sum, einsum_sum],
    n_range=[2 ** k for k in range(10)],
)


def numpy_power(a):
    return a * a * a


def einsum_power(a):
    return numpy.einsum("ijk,ijk,ijk->ijk", a, a, a)


perfplot.save(
    "power.png",
    setup=setup3,
    kernels=[numpy_power, einsum_power],
    n_range=[2 ** k for k in range(9)],
)


def numpy_outer(a):
    return numpy.outer(a, a)


def einsum_outer(a):
    return numpy.einsum("i,k->ik", a, a)


perfplot.save(
    "outer.png",
    setup=setup1,
    kernels=[numpy_outer, einsum_outer],
    n_range=[2 ** k for k in range(13)],
)


def dgemm_numpy(a):
    return numpy.dot(a, a)


def dgemm_einsum(a):
    return numpy.einsum("ij,jk", a, a)


def dgemm_einsum_optimize(a):
    return numpy.einsum("ij,jk", a, a, optimize=True)


perfplot.save(
    "dgemm.png",
    setup=setup2,
    kernels=[dgemm_numpy, dgemm_einsum],
    n_range=[2 ** k for k in range(13)],
)


def dot_numpy(a):
    return numpy.dot(a, a)


def dot_einsum(a):
    return numpy.einsum("i,i->", a, a)


perfplot.save(
    "dot.png",
    setup=setup1,
    kernels=[dot_numpy, dot_einsum],
    n_range=[2 ** k for k in range(20)],
)


def sum23_numpy(data):
    a, b = data
    return numpy.sum(a * b)


def sum23_einsum(data):
    a, b = data
    return numpy.einsum("ij,oij->", a, b)


perfplot.save(
    "sum23.png",
    setup=setup23,
    kernels=[sum23_numpy, sum23_einsum],
    n_range=[2 ** k for k in range(10)],
)

Sportscast

One note on the GEMM if you numpy.einsum("ij,jk", a, a, optimize=True) the performance will be equivalent. It is somewhat strange the latency is smaller, did the logic of this functions move to C? Also worth trying a np.einsum('i,i->', ...) as well as the np.einsum('ij,oij->' for a more apples to apples comparison. – Scour

@Scour Added those. – Orna