numpy : calculate the derivative of the softmax function

Question

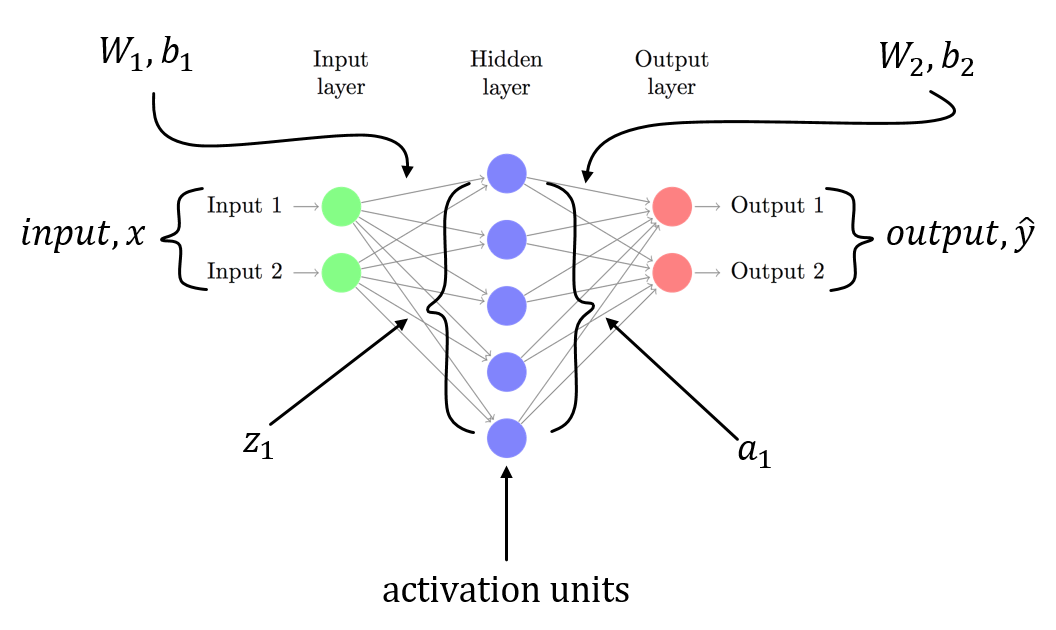
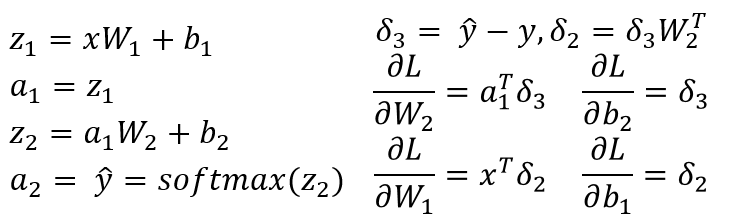I am trying to understand backpropagation in a simple 3 layered neural network with MNIST.

There is the input layer with weights and a bias. The labels are MNIST so it's a 10 class vector.

The second layer is a linear tranform. The third layer is the softmax activation to get the output as probabilities.

Backpropagation calculates the derivative at each step and call this the gradient.

Previous layers appends the global or previous gradient to the local gradient. I am having trouble calculating the local gradient of the softmax

Several resources online go through the explanation of the softmax and its derivatives and even give code samples of the softmax itself

def softmax(x):
    """Compute the softmax of vector x."""
    exps = np.exp(x)
    return exps / np.sum(exps)

The derivative is explained with respect to when i = j and when i != j. This is a simple code snippet I've come up with and was hoping to verify my understanding:

def softmax(self, x):
    """Compute the softmax of vector x."""
    exps = np.exp(x)
    return exps / np.sum(exps)

def forward(self):
    # self.input is a vector of length 10
    # and is the output of 
    # (w * x) + b
    self.value = self.softmax(self.input)

def backward(self):
    for i in range(len(self.value)):
        for j in range(len(self.input)):
            if i == j:
                self.gradient[i] = self.value[i] * (1-self.input[i))
            else: 
                 self.gradient[i] = -self.value[i]*self.input[j]

Then self.gradient is the local gradient which is a vector. Is this correct? Is there a better way to write this?

Bollworm

This is so unclear... What gradient are you actually trying to compute? SM is a map from R^n to R^n so you may define n^2 partial derivatives dSM[i]/dx[k]... – Anyway

@JulienBernu I have updated the question. Any thoughts? – Bollworm

These two links helped me in understanding these eli.thegreenplace.net/2016/… + https://mcmap.net/q/587127/-how-to-implement-the-softmax-derivative-independently-from-any-loss-function (and they are referenced in multiple places ex e2eml.school/softmax.html) – Deandeana

Answer 1

I am assuming you have a 3-layer NN with W1, b1 for is associated with the linear transformation from input layer to hidden layer and W2, b2 is associated with linear transformation from hidden layer to output layer. Z1 and Z2 are the input vector to the hidden layer and output layer. a1 and a2 represents the output of the hidden layer and output layer. a2 is your predicted output. delta3 and delta2 are the errors (backpropagated) and you can see the gradients of the loss function with respect to model parameters.

This is a general scenario for a 3-layer NN (input layer, only one hidden layer and one output layer). You can follow the procedure described above to compute gradients which should be easy to compute! Since another answer to this post already pointed to the problem in your code, i am not repeating the same.

Panek

To clarify one more thing. If we were to start with z2, i.e. z1 never existed, would that make it a 2 layer NN? The linear transform happening twice makes it a 3 layer NN? – Bollworm

Can you explain the names of the layers in your equations? The input layer in your case is z1? How many hidden layers and what are they? – Bollworm

Amazing! Thank you very much! God bless you and good luck in your PhD studies! – Bollworm

I'm going to update this library I'm putting together to match the above. github.com/autojazari/xiaonet/blob/master/xiaonet.py Will edit the question once finished – Bollworm

What is the loss function here? – Alithia

@sidmontu: I believe its cross-entropy. – Grazing

Is it really correct to call the nodes in the hidden layer "activation units" when a1 = z1? There's no activation function in that layer, it's linear. – Brunhilde

Answer 2

As I said, you have n^2 partial derivatives.

If you do the math, you find that dSM[i]/dx[k] is SM[i] * (dx[i]/dx[k] - SM[i]) so you should have:

if i == j:
    self.gradient[i,j] = self.value[i] * (1-self.value[i])
else: 
    self.gradient[i,j] = -self.value[i] * self.value[j]

instead of

if i == j:
    self.gradient[i] = self.value[i] * (1-self.input[i])
else: 
     self.gradient[i] = -self.value[i]*self.input[j]

By the way, this may be computed more concisely like so (vectorized):

SM = self.value.reshape((-1,1))
jac = np.diagflat(self.value) - np.dot(SM, SM.T)

Anyway

Ok so that is the Jacobian? – Bollworm

I think I have another disconnect. Is the linear transform in @wasi's answer the hidden layer? – Bollworm

I guess so. Note that most people consider the last linear transform + the SM as only one layer. In general a layer is a linear transform followed by a non linearity (sigmoid, tanh, SM, relu, or whatever...) – Anyway

In some implementations I saw, the output value of the softmax in the forward propagation was also being used. In your version that is not the case, only the input from the gradient of the loss function is being used. Am I missing something or is this the full formula? – Stevana

Answer 3

np.exp is not stable because it has Inf. So you should subtract maximum in x.

def softmax(x):
    """Compute the softmax of vector x."""
    exps = np.exp(x - x.max())
    return exps / np.sum(exps)

If x is matrix, please check the softmax function in this notebook.

Swingletree

Would subtracting the max value change the softmax derivative? And if not, why not? – Rider

@KBazan because the e^(x-c) = e^x.e^-c.. there is another in the denominator. So they cancel out. – Seward