How to determine whether a point (X,Y) is contained within an arc section of a circle (i.e. a Pie slice)?

Question

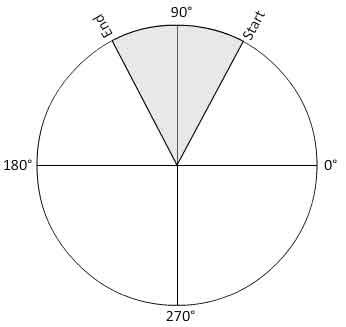
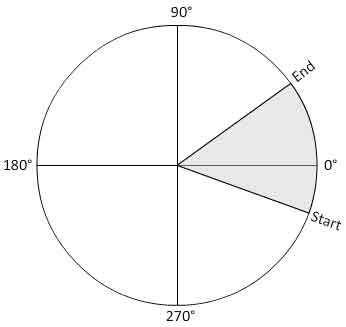
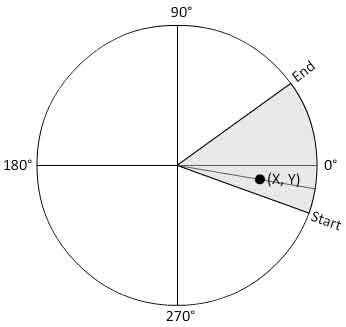
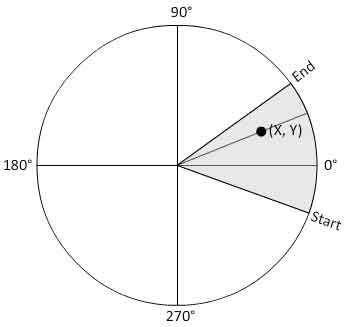
Imagine a circle. Imagine a pie. Imagine trying to return a bool that determines whether the provided parameters of X, Y are contained within one of those pie pieces.

What I know about the arc:

I have the CenterX, CenterY, Radius, StartingAngle, EndingAngle, StartingPoint (point on circumference), EndingPoint (point on circumference).

Given a coordinate of X,Y, I'd like to determine if this coordinate is contained anywhere within the pie slide.

Most

Why are C# and Java tagged? This looks just like a plain Math question. – Nonillion

Whoops. I'd originally had the question as language-specific, but then changed it around to be more generic. Forgot to edit the tags. Apologies. – Most

Answer 1

I know this question is old but none of the answers consider the placement of the arc on the circle.

This algorithm considers that all angles are between 0 and 360, and the arcs are drawn in positive mathematical direction (counter-clockwise)

First you can transform to polar coordinates: radius (R) and angle (A). Note: use Atan2 function if available. wiki

R = sqrt ((X - CenterX)^2 + (Y - CenterY)^2)

A = atan2 (Y - CenterY, X - CenterX)

Now if R < Radius the point is inside the circle.

To check if the angle is between StartingAngle (S) and EndingAngle (E) you need to consider two possibilities:

1) if S < E then if S < A < E the point lies inside the slice

2) if S > E then there are 2 possible scenarios

• if A > S

then the point lies inside the slice

• if A < E

then the point lies inside the slice

In all other cases the point lies outside the slice.

Tannenbaum

I was thinking about this exact question, and you are absolutely right! – Most

@chux-ReinstateMonica You are correct. I didn't see that before – Tannenbaum

Why couldn't you just do : angle from start < angle between start and end = is in between ? I seen no reason for all these if else edge cases. – Tsan

@WDUK, Say you have a slice starting at 350 degrees and ending at 30 degrees. Lets say your point lies at 15 degrees. It is inside the slice but 350<15<30 is not true. – Tannenbaum

The problem i have with this is say you want to define an arc, you can't really define some of those images with those degrees. For example the very last image you cannot define an arc as being "between 300 and 35 degrees" since that wouldn't make sense unless it was a clockwise arc. – Tsan

There is an identity between angles 0 = 360, 35 = 395, 300 = 660... You use screen coordinates (X,Y) to draw the arc in code, not angles directly. When writing code, it's easier to keep the angles in the range 0 - 360, to avoid having to think about when to reduce or when to keep the angle as is - it becomes unnecessarily complicated. – Tannenbaum

But say your start angle is at 270 and your end angle is at 45, thats kinda confusing (assuming counter clockwise) in terms of how you travel between the two you couldn't just lerp between them like angle = (start,end,t) with t = [0,1] i feel like it is better to always make sure end angle is greater than the start angle any where on the circle. @Tannenbaum – Tsan

Answer 2

Check:

1. The angle from the centerX,centerY through X,Y should be between start&endangle.
2. The distance from centerX,centerY to X,Y should be less then the Radius

And you'll have your answer.

Incorporeal

@Wrikken, how to determine that one angle is between two other angles, using equations? – Nailbrush

@Demian: This is a bit old, but you can find an answer here: math.stackexchange.com/questions/1596513/… – Ewan

Answer 3

Convert X,Y to polar coordinates using this:

Angle = arctan(y/x); Radius = sqrt(x * x + y * y);

Then Angle must be between StartingAngle and EndingAngle, and Radius between 0 and your Radius.

Decontaminate

Instead of Radius = sqrt(x * x + y * y); You can try (x*x+y*y)<=r*r – Awl

Answer 4

You have to convert atan2() to into 0-360 before making comparisons with starting and ending angles.

(A > 0 ? A : (2PI + A)) * 360 / (2PI)

Canopy

if atan2 is already converted to 0-360, isn't (A > 0) condition unnecessary ? – Lance

No. The atan2() function returns a value in the range -π to π radians. – Canopy