The other answers here have done a great job presenting the O(n)-time, O(n)-space solution using two stacks. There's another perspective on this problem that independently provides an O(n)-time, O(n)-space solution to the problem, and might provide a little bit more insight as to why the stack-based solution works.
The key idea is to use a data structure called a Cartesian tree. A Cartesian tree is a binary tree structure (though not a binary search tree) that's built around an input array. Specifically, the root of the Cartesian tree is built above the minimum element of the array, and the left and right subtrees are recursively constructed from the subarrays to the left and right of the minimum value.
For example, here's a sample array and its Cartesian tree:
+----------------------- 23 ------+
| |
+------------- 26 --+ +-- 79
| | |
31 --+ 53 --+ 84
| |
41 --+ 58 -------+
| |
59 +-- 93
|
97
+----+----+----+----+----+----+----+----+----+----+----+
| 31 | 41 | 59 | 26 | 53 | 58 | 97 | 93 | 23 | 84 | 79 |
+----+----+----+----+----+----+----+----+----+----+----+
The reason that Cartesian trees are useful in this problem is that the question at hand has a really nice recursive structure to it. Begin by looking at the lowest rectangle in the histogram. There are three options for where the maximum rectangle could end up being placed:
It could pass right under the minimum value in the histogram. In that case, to make it as large as possible, we'd want to make it as wide as the entire array.
It could be entirely to the left of the minimum value. In that case, we recursively want the answer formed from the subarray purely to the left of the minimum value.
It could be entirely to the right of the minimum value. In that case, we recursively want the answer formed from the subarray purely to the right of the minimum value.
Notice that this recursive structure - find the minimum value, do something with the subarrays to the left and the right of that value - perfectly matches the recursive structure of a Cartesian tree. In fact, if we can create a Cartesian tree for the overall array when we get started, we can then solve this problem by recursively walking the Cartesian tree from the root downward. At each point, we recursively compute the optimal rectangle in the left and right subarrays, along with the rectangle you'd get by fitting right under the minimum value, and then return the best option we find.
In pseudocode, this looks like this:
function largestRectangleUnder(int low, int high, Node root) {
/* Base case: If the range is empty, the biggest rectangle we
* can fit is the empty rectangle.
*/
if (low == high) return 0;
/* Assume the Cartesian tree nodes are annotated with their
* positions in the original array.
*/
return max {
(high - low) * root.value, // Widest rectangle under the minimum
largestRectangleUnder(low, root.index, root.left),
largestRectnagleUnder(root.index + 1, high, root.right)
}
}
Once we have the Cartesian tree, this algorithm takes time O(n), since we visit each node exactly once and do O(1) work per node.
It turns out that there's a simple, linear-time algorithm for building Cartesian trees. The "natural" way you'd probably think to build one would be to scan across the array, find the minimum value, then recursively build a Cartesian tree from the left and right subarrays. The problem is that the process of finding the minimum value is really expensive, and this can take time Θ(n2).
The "fast" way to build a Cartesian tree is by scanning the array from the left to the right, adding in one element at a time. This algorithm is based on the following observations about Cartesian trees:
First, Cartesian trees obey the heap property: every element is less than or equal to its children. The reason for this is that the Cartesian tree root is the smallest value in the overall array, and its children are the smallest elements in their subarrays, etc.
Second, if you do an inorder traversal of a Cartesian tree, you get back the elements of the array in the order in which they appear. To see why this is, notice that if you do an inorder traversal of a Cartesian tree, you first visit everything to the left of the minimum value, then the minimum value, then everything to the right of the minimum value. Those visitations are recursively done the same way, so everything ends up being visited in order.
These two rules give us a lot of information about what happens if we start with a Cartesian tree of the first k elements of the array and want to form a Cartesian tree for the first k+1 elements. That new element will have to end up on the right spine of the Cartesian tree - the part of the tree formed by starting at the root and only taking steps to the right - because otherwise something would come after it in an inorder traversal. And, within that right spine, it has to be placed in a way that makes it bigger than everything above it, since we need to obey the heap property.
The way that you actually add a new node to the Cartesian tree is to start at the rightmost node in the tree and walk upwards until you either hit the root of the tree or find a node that has a smaller value. You then make the new value have as its left child the last node it walked up on top of.
Here's a trace of that algorithm on a small array:
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
2 becomes the root.
2 --+
|
4
4 is bigger than 2, we can't move upwards. Append to right.
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
2 ------+
|
--- 3
|
4
3 is lesser than 4, climb over it. Can't climb further over 2, as it is smaller than 3. Climbed over subtree rooted at 4 goes to the left of new value 3 and 3 becomes rightmost node now.
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
+---------- 1
|
2 ------+
|
--- 3
|
4
1 climbs over the root 2, the entire tree rooted at 2 is moved to left of 1, and 1 is now the new root - and also the rightmost value.
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
Although this might not seem to run in linear time - wouldn't you potentially end up climbing all the way to the root of the tree over and over and over again? - you can show that this runs in linear time using a clever argument. If you climb up over a node in the right spine during an insertion, that node ends up getting moved off the right spine and therefore can't be rescanned in a future insertion. Therefore, every node is only ever scanned over at most once, so the total work done is linear.
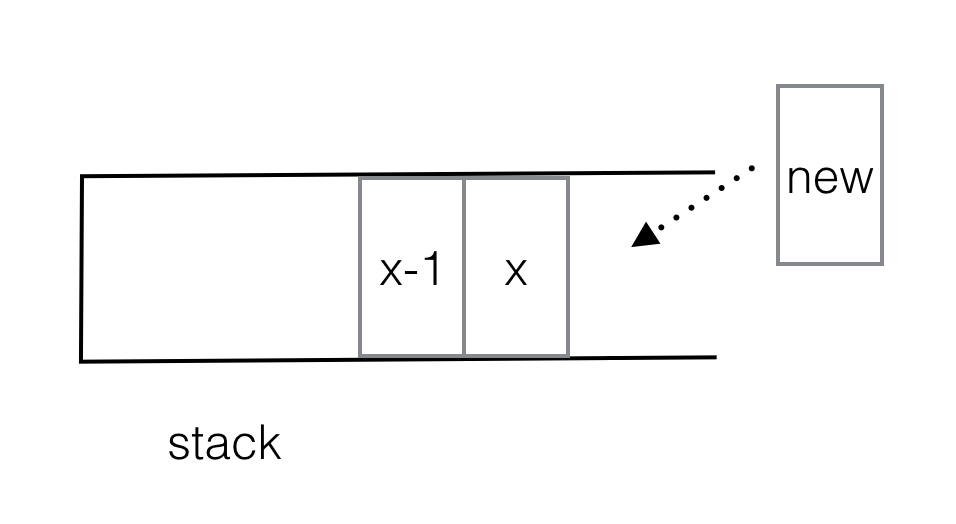
And now the kicker - the standard way that you'd actually implement this approach is by maintaining a stack of the values that correspond to the nodes on the right spine. The act of "walking up" and over a node corresponds to popping a node off the stack. Therefore, the code for building a Cartesian tree looks something like this:
Stack s;
for (each array element x) {
pop s until it's empty or s.top > x
push x onto the stack.
do some sort of pointer rewiring based on what you just did.
}
The stack manipulations here might seem really familiar, and that's because these are the exact stack operations that you would do in the answers shown elsewhere here. In fact, you can think of what those approaches are doing as implicitly building the Cartesian tree and running the recursive algorithm shown above in the process of doing so.
The advantage, I think, of knowing about Cartesian trees is that it provides a really nice conceptual framework for seeing why this algorithm works correctly. If you know that what you're doing is running a recursive walk of a Cartesian tree, it's easier to see that you're guaranteed to find the largest rectangle. Plus, knowing that the Cartesian tree exists gives you a useful tool for solving other problems. Cartesian trees show up in the design of fast data structures for the range minimum query problem and are used to convert suffix arrays into suffix trees.
Here's some Java code that implements this idea, courtesy of @Azeem!
import java.util.Stack;
public class CartesianTreeMakerUtil {
private static class Node {
int val;
Node left;
Node right;
}
public static Node cartesianTreeFor(int[] nums) {
Node root = null;
Stack<Node> s = new Stack<>();
for(int curr : nums) {
Node lastJumpedOver = null;
while(!s.empty() && s.peek().val > curr) {
lastJumpedOver = s.pop();
}
Node currNode = this.new Node();
currNode.val = curr;
if(s.isEmpty()) {
root = currNode;
}
else {
s.peek().right = currNode;
}
currNode.left = lastJumpedOver;
s.push(currNode);
}
return root;
}
public static void printInOrder(Node root) {
if(root == null) return;
if(root.left != null ) {
printInOrder(root.left);
}
System.out.println(root.val);
if(root.right != null) {
printInOrder(root.right);
}
}
public static void main(String[] args) {
int[] nums = new int[args.length];
for (int i = 0; i < args.length; i++) {
nums[i] = Integer.parseInt(args[i]);
}
Node root = cartesianTreeFor(nums);
tester.printInOrder(root);
}
}

O(n log n)andO(n). – Carroty