Inverse of a matrix in SymPy?

Question

I was wondering how to create a matrix and compute its inverse using SymPy in Python?

For example, for this symbolic matrix:

Gallenz

Answer 1

If your question was: How to compute the inverse of a matrix M in sympy then:

M_inverse = M.inv()

As for how to create a matrix:

M = Matrix(2,3, [1,2,3,4,5,6])

will give you the following 2X3 matrix:

1 2 3

4 5 6

See: http://docs.sympy.org/0.7.2/modules/matrices/matrices.html

Pemberton

What is the difference between M.inv() and Inverse(M)? – Ruddy

@Ruddy I'm not sure, if related, but have a look: #50855303 – Jimmie

Answer 2

Here is example of how we can compute inverse for a symbolic matrix (taking the one from the question):

import sympy as sym


# Not necessary but gives nice-looking latex output
# More info at: http://docs.sympy.org/latest/tutorial/printing.html
sym.init_printing()

sx, sy, rho = sym.symbols('sigma_x sigma_y rho')
matrix = sym.Matrix([[sx ** 2, rho * sx * sy], 
                     [rho * sx * sy, sy ** 2]])

Now printing the inverse matrix.inv() will give:
                                      

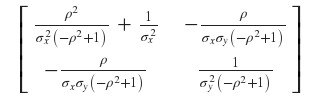
which can be further simplified like sym.simplify(matrix.inv()):
                                                

Quickfreeze

Answer 3

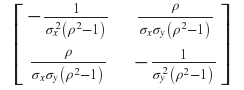
The available sympy methods are very slow for symbolic matrices. Entry-wise operations are way faster. I found it in this paper by the name of 'partial inversion': doi.org/10.1088/1402-4896/ad298a.

Here's the code and a graph of time performance for symbolic matrices of dimensions (2,2) and (3,3). (The .inv() method wouldn't finish compiling for me for higher dimensions, whereas the 'partial inversion' does the job reasonably quick.)

from sympy import Matrix, Symbol, simplify

def sp_partial_inversion(m, *cells):
    ''' Partial inversion algorithm.
    ARGUMENTS
        m <sympy.Matrix> : symbolic matrix
        *cells <tuple>   : 2-tuples with matrix indices to perform partial inversion on.
    RETURNS
        <sympy.Matrix>   : matrix m partially-inverted at indices *cells
    '''
    # Partial inversion algorithm
    M = m.copy()
    for cell in cells:
        i,k = cell
        z = M[i,k]
        newmat = []
        for r in range(m.shape[0]):
            newrow = []
            for c in range(m.shape[1]):
                if i == r:
                    if k == c:  # Pivot cell
                        newrow.append( 1/z )
                    else:       # Pivot row
                        newrow.append( -M[r,c]/z )
                else:
                    if k == c:  # Pivot col
                        newrow.append( M[r,c]/z )
                    else:       # Elsewhere
                        newrow.append( M[r,c] - M[i,c]*M[r,k]/z )
            newmat.append(newrow)
        M =  Matrix(newmat)
    #
    return M

def SymbolicMatrix(n):
    "Generates symbolic matrix for tests"
    return Matrix( [ Symbol( f'm_{i}' ) for i in range(n**2) ] ).reshape(n,n)

def FullInversion(m):
    "Full matrix inversion is partial inversion at all i==j."
    cells = [(i,i) for i in range(m.shape[0])]
    return sp_partial_inversion(m, *cells)

# Test 1 --- Z should be matrix of zeros
M = SymbolicMatrix(3)
#Z = simplify( FullInversion(M) - M.inv() )

# Test 2 ---
M = SymbolicMatrix(4)
M_ = simplify( FullInversion(M) )
M_

Check the plots:

Figure of time performance plot for 1000 sympy symbolic matrices from (2,2) to (3,3).

Figure of time performance plot for 100 sympy symbolic matrices from (2,2) to (4,4).

It can also be used for numerical matrices, but it's not faster than numpy's default matrix inversion in my tests.

Refined