Normal equation and Numpy 'least-squares', 'solve' methods difference in regression?

Asked 9/12, 2015 at 4:16 Answered 17/10, 2016 at 5:31

Solved python numpy machine-learning linear-algebra linear-regression

I am doing linear regression with multiple variables/features. I try to get thetas (coefficients) by using normal equation method (that uses matrix inverse), Numpy least-squares numpy.linalg.lstsq tool and np.linalg.solve tool. In my data I have n = 143 features and m = 13000 training examples.

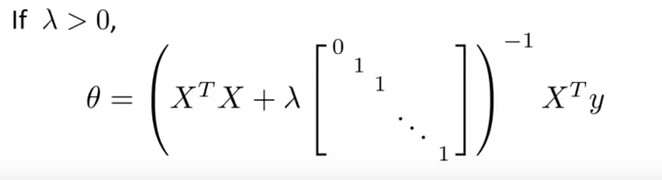
For normal equation method with regularization I use this formula:

Sources:

Regularization (Andrew Ng, Stanford)

Normal equations (Andrew Ng, Stanford)

Regularization is used to solve the potential problem of matrix non-invertibility (XtX matrix may become singular/non-invertible)

Data preparation code:

import pandas as pd
import numpy as np

path = 'DB2.csv'  
data = pd.read_csv(path, header=None, delimiter=";")

data.insert(0, 'Ones', 1)
cols = data.shape[1]

X = data.iloc[:,0:cols-1]  
y = data.iloc[:,cols-1:cols] 

IdentitySize = X.shape[1]
IdentityMatrix= np.zeros((IdentitySize, IdentitySize))
np.fill_diagonal(IdentityMatrix, 1)

For least squares method I use Numpy's numpy.linalg.lstsq. Here is Python code:

lamb = 1
th = np.linalg.lstsq(X.T.dot(X) + lamb * IdentityMatrix, X.T.dot(y))[0]

Also I used np.linalg.solve tool of numpy:

lamb = 1
XtX_lamb = X.T.dot(X) + lamb * IdentityMatrix
XtY = X.T.dot(y)
x = np.linalg.solve(XtX_lamb, XtY);

For normal equation I use:

lamb = 1
xTx = X.T.dot(X) + lamb * IdentityMatrix
XtX = np.linalg.inv(xTx)
XtX_xT = XtX.dot(X.T)
theta = XtX_xT.dot(y)

In all methods I used regularization. Here is results (theta coefficients) to see difference between these three approaches:

Normal equation:        np.linalg.lstsq         np.linalg.solve
[-27551.99918303]       [-27551.95276154]       [-27551.9991855]
[-940.27518383]         [-940.27520138]         [-940.27518383]
[-9332.54653964]        [-9332.55448263]        [-9332.54654461]
[-3149.02902071]        [-3149.03496582]        [-3149.02900965]
[-1863.25125909]        [-1863.2631435]         [-1863.25126344]
[-2779.91105618]        [-2779.92175308]        [-2779.91105347]
[-1226.60014026]        [-1226.61033117]        [-1226.60014192]
[-920.73334259]         [-920.74331432]         [-920.73334194]
[-6278.44238081]        [-6278.45496955]        [-6278.44237847]
[-2001.48544938]        [-2001.49566981]        [-2001.48545349]
[-715.79204971]         [-715.79664124]         [-715.79204921]
[ 4039.38847472]        [ 4039.38302499]        [ 4039.38847515]
[-2362.54853195]        [-2362.55280478]        [-2362.54853139]
[-12730.8039209]        [-12730.80866036]       [-12730.80392076]
[-24872.79868125]       [-24872.80203459]       [-24872.79867954]
[-3402.50791863]        [-3402.5140501]         [-3402.50793382]
[ 253.47894001]         [ 253.47177732]         [ 253.47892472]
[-5998.2045186]         [-5998.20513905]        [-5998.2045184]
[ 198.40560401]         [ 198.4049081]          [ 198.4056042]
[ 4368.97581411]        [ 4368.97175688]        [ 4368.97581426]
[-2885.68026222]        [-2885.68154407]        [-2885.68026205]
[ 1218.76602731]        [ 1218.76562838]        [ 1218.7660275]
[-1423.73583813]        [-1423.7369068]         [-1423.73583793]
[ 173.19125007]         [ 173.19086525]         [ 173.19125024]
[-3560.81709538]        [-3560.81650156]        [-3560.8170952]
[-142.68135768]         [-142.68162508]         [-142.6813575]
[-2010.89489111]        [-2010.89601322]        [-2010.89489092]
[-4463.64701238]        [-4463.64742877]        [-4463.64701219]
[ 17074.62997704]       [ 17074.62974609]       [ 17074.62997723]
[ 7917.75662561]        [ 7917.75682048]        [ 7917.75662578]
[-4234.16758492]        [-4234.16847544]        [-4234.16758474]
[-5500.10566329]        [-5500.106558]          [-5500.10566309]
[-5997.79002683]        [-5997.7904842]         [-5997.79002634]
[ 1376.42726683]        [ 1376.42629704]        [ 1376.42726705]
[ 6056.87496151]        [ 6056.87452659]        [ 6056.87496175]
[ 8149.0123667]         [ 8149.01209157]        [ 8149.01236827]
[-7273.3450484]         [-7273.34480382]        [-7273.34504827]
[-2010.61773247]        [-2010.61839251]        [-2010.61773225]
[-7917.81185096]        [-7917.81223606]        [-7917.81185084]
[ 8247.92773739]        [ 8247.92774315]        [ 8247.92773722]
[ 1267.25067823]        [ 1267.24677734]        [ 1267.25067832]
[ 2557.6208133]         [ 2557.62126916]        [ 2557.62081337]
[-5678.53744654]        [-5678.53820798]        [-5678.53744647]
[ 3406.41697822]        [ 3406.42040997]        [ 3406.41697836]
[-8371.23657044]        [-8371.2361594]         [-8371.23657035]
[ 15010.61728285]       [ 15010.61598236]       [ 15010.61728304]
[ 11006.21920273]       [ 11006.21711213]       [ 11006.21920284]
[-5930.93274062]        [-5930.93237071]        [-5930.93274048]
[-5232.84459862]        [-5232.84557665]        [-5232.84459848]
[ 3196.89304277]        [ 3196.89414431]        [ 3196.8930428]
[ 15298.53309912]       [ 15298.53496877]       [ 15298.53309919]
[ 4742.68631183]        [ 4742.6862601]         [ 4742.68631172]
[ 4423.14798495]        [ 4423.14765013]        [ 4423.14798546]
[-16153.50854089]       [-16153.51038489]       [-16153.50854123]
[-22071.50792741]       [-22071.49808389]       [-22071.50792408]
[-688.22903323]         [-688.2310229]          [-688.22904006]
[-1060.88119863]        [-1060.8829114]         [-1060.88120546]
[-101.75750066]         [-101.75776411]         [-101.75750831]
[ 4106.77311898]        [ 4106.77128502]        [ 4106.77311218]
[ 3482.99764601]        [ 3482.99518758]        [ 3482.99763924]
[-1100.42290509]        [-1100.42166312]        [-1100.4229119]
[ 20892.42685103]       [ 20892.42487476]       [ 20892.42684422]
[-5007.54075789]        [-5007.54265501]        [-5007.54076473]
[ 11111.83929421]       [ 11111.83734144]       [ 11111.83928704]
[ 9488.57342568]        [ 9488.57158677]        [ 9488.57341883]
[-2992.3070786]         [-2992.29295891]        [-2992.30708529]
[ 17810.57005982]       [ 17810.56651223]       [ 17810.57005457]
[-2154.47389712]        [-2154.47504319]        [-2154.47390285]
[-5324.34206726]        [-5324.33913623]        [-5324.34207293]
[-14981.89224345]       [-14981.8965674]        [-14981.89224973]
[-29440.90545197]       [-29440.90465897]       [-29440.90545704]
[-6925.31991443]        [-6925.32123144]        [-6925.31992383]
[ 104.98071593]         [ 104.97886085]         [ 104.98071152]
[-5184.94477582]        [-5184.9447972]         [-5184.94477792]
[ 1555.54536625]        [ 1555.54254362]        [ 1555.5453638]
[-402.62443474]         [-402.62539068]         [-402.62443718]
[ 17746.15769322]       [ 17746.15458093]       [ 17746.15769074]
[-5512.94925026]        [-5512.94980649]        [-5512.94925267]
[-2202.8589276]         [-2202.86226244]        [-2202.85893056]
[-5549.05250407]        [-5549.05416936]        [-5549.05250669]
[-1675.87329493]        [-1675.87995809]        [-1675.87329255]
[-5274.27756529]        [-5274.28093377]        [-5274.2775701]
[-5424.10246845]        [-5424.10658526]        [-5424.10247326]
[-1014.70864363]        [-1014.71145066]        [-1014.70864845]
[ 12936.59360437]       [ 12936.59168749]       [ 12936.59359954]
[ 2912.71566077]        [ 2912.71282628]        [ 2912.71565599]
[ 6489.36648506]        [ 6489.36538259]        [ 6489.36648021]
[ 12025.06991281]       [ 12025.07040848]       [ 12025.06990358]
[ 17026.57841531]       [ 17026.56827742]       [ 17026.57841044]
[ 2220.1852193]         [ 2220.18531961]        [ 2220.18521579]
[-2886.39219026]        [-2886.39015388]        [-2886.39219394]
[-18393.24573629]       [-18393.25888463]       [-18393.24573872]
[-17591.33051471]       [-17591.32838012]       [-17591.33051834]
[-3947.18545848]        [-3947.17487999]        [-3947.18546459]
[ 7707.05472816]        [ 7707.05577227]        [ 7707.0547217]
[ 4280.72039079]        [ 4280.72338194]        [ 4280.72038435]
[-3137.48835901]        [-3137.48480197]        [-3137.48836531]
[ 6693.47303443]        [ 6693.46528167]        [ 6693.47302811]
[-13936.14265517]       [-13936.14329336]       [-13936.14267094]
[ 2684.29594641]        [ 2684.29859601]        [ 2684.29594183]
[-2193.61036078]        [-2193.63086307]        [-2193.610366]
[-10139.10424848]       [-10139.11905454]       [-10139.10426049]
[ 4475.11569903]        [ 4475.12288711]        [ 4475.11569421]
[-3037.71857269]        [-3037.72118246]        [-3037.71857265]
[-5538.71349798]        [-5538.71654224]        [-5538.71349794]
[ 8008.38521357]        [ 8008.39092739]        [ 8008.38521361]
[-1433.43859633]        [-1433.44181824]        [-1433.43859629]
[ 4212.47144667]        [ 4212.47368097]        [ 4212.47144686]
[ 19688.24263706]       [ 19688.2451694]        [ 19688.2426368]
[ 104.13434091]         [ 104.13434349]         [ 104.13434091]
[-654.02451175]         [-654.02493111]         [-654.02451174]
[-2522.8642551]         [-2522.88694451]        [-2522.86424254]
[-5011.20385919]        [-5011.22742915]        [-5011.20384655]
[-13285.64644021]       [-13285.66951459]       [-13285.64642763]
[-4254.86406891]        [-4254.88695873]        [-4254.86405637]
[-2477.42063206]        [-2477.43501057]        [-2477.42061727]
[ 0.]                   [  1.23691279e-10]      [ 0.]
[-92.79470071]          [-92.79467095]          [-92.79470071]
[ 2383.66211583]        [ 2383.66209637]        [ 2383.66211583]
[-10725.22892185]       [-10725.22889937]       [-10725.22892185]
[ 234.77560283]         [ 234.77560254]         [ 234.77560283]
[ 4739.22119578]        [ 4739.22121432]        [ 4739.22119578]
[ 43640.05854156]       [ 43640.05848841]       [ 43640.05854157]
[ 2592.3866707]         [ 2592.38671547]        [ 2592.3866707]
[-25130.02819215]       [-25130.05501178]       [-25130.02819515]
[ 4966.82173096]        [ 4966.7946407]         [ 4966.82172795]
[ 14232.97930665]       [ 14232.9529959]        [ 14232.97930363]
[-21621.77202422]       [-21621.79840459]       [-21621.7720272]
[ 9917.80960029]        [ 9917.80960571]        [ 9917.80960029]
[ 1355.79191536]        [ 1355.79198092]        [ 1355.79191536]
[-27218.44185748]       [-27218.46880642]       [-27218.44185719]
[-27218.04184348]       [-27218.06875423]       [-27218.04184318]
[ 23482.80743869]       [ 23482.78043029]       [ 23482.80743898]
[ 3401.67707434]        [ 3401.65134677]        [ 3401.67707463]
[ 3030.36383274]        [ 3030.36384909]        [ 3030.36383274]
[-30590.61847724]       [-30590.63933424]       [-30590.61847706]
[-28818.3942685]        [-28818.41520495]       [-28818.39426833]
[-25115.73726772]       [-25115.7580278]        [-25115.73726753]
[ 77174.61695995]       [ 77174.59548773]       [ 77174.61696016]
[-20201.86613672]       [-20201.88871113]       [-20201.86613657]
[ 51908.53292209]       [ 51908.53446495]       [ 51908.53292207]
[ 7710.71327865]        [ 7710.71324194]        [ 7710.71327865]
[-16206.9785119]        [-16206.97851993]       [-16206.9785119]

As you can see normal equation, least squares and np.linalg.solve tool methods give to some extent different results. The question is why these three approaches gives noticeably different results and which method gives more efficient and more accurate result?

Assumption: Results of Normal equation method and results of np.linalg.solve are very close to each other. And results of np.linalg.lstsq differ from both of them. Since normal equation uses inverse we do not expect very accurate results of it and therefore results of np.linalg.solve tool also. Seem to be that better results are given by np.linalg.lstsq.

Upd:
As Dave Hensley mentioned:
After the line np.fill_diagonal(IdentityMatrix, 1) this code IdentityMatrix[0,0] = 0 should be added.

DB2.csv is available on DropBox: DB2.csv

Full Python code is available on DropBox: Full code

Rework answered 9/12, 2015 at 4:16 Comment(2)

Out of curiosity, is DB2.csv anywhere we can download? – Thad 9/12, 2015 at 6:0

I uploaded DB2.csv to google drive: drive.google.com/open?id=0BzzUvSbpsTAvN1UxTkxXd2U0eVE – Rework 9/12, 2015 at 6:5

As @Matthew Gunn mentioned, it's bad practice to compute the explicit inverse of your coefficient matrix as a means to solve linear systems of equations. It's faster and more accurate to obtain the solution directly (see here).

The reason why you see differences between np.linalg.solve and np.linalg.lstsq is because these functions make different assumptions about the system you are trying to solve, and use different numerical methods.

Under the hood, solve calls the DGESV LAPACK routine, which uses LU factorization, followed by forward and backward substitution to find an exact solution to Ax = b. It requires that the system is exactly determined, i.e. that A is square and of full rank.
lstsq instead calls DGELSD, which uses the singular value decomposition of A in order to find a least-squares solution. This also works in overdetermined and underdetermined cases.

If your system is fully determined then you should use solve since it requires fewer floating point operations, and will therefore be faster and more precise. In your case, XtX_lamb is guaranteed to be full rank because of the regularisation step.

Disproportionation answered 1/10, 2016 at 9:56 Comment(1)

full rank OK, but the choice of lambda_regularization_param - in order not to over-regularize or under-regularize - is it possible to find out with either solve or lstsq? I think not – Luckin 29/5 at 17:27

Don't calculate matrix inverse to solve linear systems

The professional algorithms don't solve for the matrix inverse. It's slow and introduces unnecessary error. It's not a disaster for small systems, but why do something suboptimal?

Basically anytime you see the math written as:

x = A^-1 * b

you instead want:

x = np.linalg.solve(A, b)

In you case, you want something like:

XtX_lamb = X.T.dot(X) + lamb * IdentityMatrix
XtY = X.T.dot(Y)
x = np.linalg.solve(XtX_lamb, XtY);

Thad answered 9/12, 2015 at 5:29 Comment(6)

np.linalg.lstsq tool of Numpy does not use inverse for solving equations. I used np.linalg.lstsq and your suggestion np.linalg.solve. They both give different results. What is more efficient and accurate method np.linalg.solve or np.linalg.lstsq? – Rework 9/12, 2015 at 5:51

I updated question to see difference of three approaches. – Rework 9/12, 2015 at 5:51

Another way to see how different two vectors x1 and x2 are is to subtract x2 from x1 then take the norm using numpy.linalg.norm. – Thad 9/12, 2015 at 5:53

One interesting thing is that results of np.linalg.solve tool are actually closer to Normal equation results that use inverse. Seem to be that better results are given by np.linalg.lstsq. – Rework 9/12, 2015 at 5:53

@MatthewGunn How would you change this if the data is complex and you wanted to conjugate multiply? – Fritzie 11/9, 2021 at 14:17

@Fritzie For complex matrices, a number of formulas involve the conjugate transpose rather than the simple transpose .T. I believe everything should go through with complex values in numpy (eg. it should do something like calling LAPACK cgesv instead of dgesv), but I honestly don't know all the details or if there are any issues off the top of my head without spending some time on it. – Thad 11/9, 2021 at 16:22

Under the hood, solve calls the DGESV LAPACK routine, which uses LU factorization, followed by forward and backward substitution to find an exact solution to Ax = b. It requires that the system is exactly determined, i.e. that A is square and of full rank.
lstsq instead calls DGELSD, which uses the singular value decomposition of A in order to find a least-squares solution. This also works in overdetermined and underdetermined cases.

Disproportionation answered 1/10, 2016 at 9:56 Comment(1)

The other answers define why in theory one calculation method is better than to other. However they don't give a way to test which solution actually shows better results. Here it is:

def test(a, x, b):
    res = a.dot(x).as_matrix() - b.as_matrix()
    print(np.linalg.norm(res))

test(XtX_lamb, x, XtY)
test(XtX_lamb, th, XtY)
test(XtX_lamb, theta, XtY)

This calcluates the norm2 of the error vector of the linear system. Results are:

np.linalg.solve - 0.000488340357871
np.linalg.lstsq - 1.75520748498
normal equation - 16.1628614202

Thus linalg.solve indeed show the most accurate result.

Annora answered 3/10, 2016 at 11:34 Comment(0)

I think you have a bug in your implementation which is affecting all 3 calculations. You use the following code to generate IdentityMatrix:

IdentityMatrix= np.zeros((IdentitySize, IdentitySize))
np.fill_diagonal(IdentityMatrix, 1)

(you could actually simplify that as IdentityMatrix=np.eye(IdentitySize))

The identity matrix is this (when IdentitySize == 3):

1 0 0
0 1 0
0 0 1

But what you should be using is this (same thing but with 0 in the top left):

0 0 0
0 1 0
0 0 1

Moulton answered 17/10, 2016 at 5:31 Comment(0)

Hot tags

Godot Unity Godot Help Programming Godot 4.X GUI GDScript 3D 2D Physics CSharp Godot 3.X VR XR Projects C++

Don't calculate matrix inverse to solve linear systems

Recommended topics

Hot tags