How to traverse cyclic directed graphs with modified DFS algorithm

Question

OVERVIEW

I'm trying to figure out how to traverse directed cyclic graphs using some sort of DFS iterative algorithm. Here's a little mcve version of what I currently got implemented (it doesn't deal with cycles):

class Node(object):

    def __init__(self, name):
        self.name = name

    def start(self):
        print '{}_start'.format(self)

    def middle(self):
        print '{}_middle'.format(self)

    def end(self):
        print '{}_end'.format(self)

    def __str__(self):
        return "{0}".format(self.name)


class NodeRepeat(Node):

    def __init__(self, name, num_repeats=1):
        super(NodeRepeat, self).__init__(name)
        self.num_repeats = num_repeats


def dfs(graph, start):
    """Traverse graph from start node using DFS with reversed childs"""

    visited = {}
    stack = [(start, "")]
    while stack:
        # To convert dfs -> bfs
        # a) rename stack to queue
        # b) pop becomes pop(0)
        node, parent = stack.pop()
        if parent is None:
            if visited[node] < 3:
                node.end()
            visited[node] = 3
        elif node not in visited:
            if visited.get(parent) == 2:
                parent.middle()
            elif visited.get(parent) == 1:
                visited[parent] = 2

            node.start()
            visited[node] = 1

            stack.append((node, None))

            # Maybe you want a different order, if it's so, don't use reversed
            childs = reversed(graph.get(node, []))
            for child in childs:
                if child not in visited:
                    stack.append((child, node))


if __name__ == "__main__":
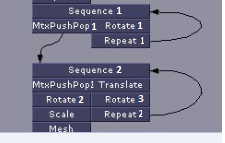
    Sequence1 = Node('Sequence1')
    MtxPushPop1 = Node('MtxPushPop1')
    Rotate1 = Node('Rotate1')
    Repeat1 = NodeRepeat('Repeat1', num_repeats=2)

    Sequence2 = Node('Sequence2')
    MtxPushPop2 = Node('MtxPushPop2')
    Translate = Node('Translate')
    Rotate2 = Node('Rotate2')
    Rotate3 = Node('Rotate3')
    Scale = Node('Scale')
    Repeat2 = NodeRepeat('Repeat2', num_repeats=3)
    Mesh = Node('Mesh')

    cyclic_graph = {
        Sequence1: [MtxPushPop1, Rotate1],
        MtxPushPop1: [Sequence2],
        Rotate1: [Repeat1],
        Sequence2: [MtxPushPop2, Translate],
        Repeat1: [Sequence1],
        MtxPushPop2: [Rotate2],
        Translate: [Rotate3],
        Rotate2: [Scale],
        Rotate3: [Repeat2],
        Scale: [Mesh],
        Repeat2: [Sequence2]
    }

    dfs(cyclic_graph, Sequence1)

    print '-'*80

    a = Node('a')
    b = Node('b')
    dfs({
        a : [b],
        b : [a]
    }, a)

The above code is testing a couple of cases, the first would be some sort of representation of the below graph:

The second one is the simplest case of one graph containing one "infinite" loop {a->b, b->a}

REQUIREMENTS

• There won't exist such a thing like "infinite cycles", let's say when one "infinite cycle" is found, there will be a maximum threshold (global var) to indicate when to stop looping around those "pseudo-infinite cycles"
• All graph nodes are able to create cycles but there will exist a special node called Repeat where you can indicate how many iterations to loop around the cycle
• The above mcve I've posted is an iterative version of the traversal algorithm which doesn't know how to deal with cyclic graphs. Ideally the solution would be also iterative but if there exists a much better recursive solution, that'd be great
• The data structure we're talking about here shouldn't be called "directed acyclic graphs" really because in this case, each node has its children ordered, and in graphs node connections have no order.
• Everything can be connected to anything in the editor. You'll be able to execute any block combination and the only limitation is the execution counter, which will overflow if you made neverending loop or too many iterations.
• The algorithm will preserve start/middle/after node's method execution similarly than the above snippet

QUESTION

Could anyone provide some sort of solution which knows how to traverse infinite/finite cycles?

REFERENCES

If question is not clear yet at this point, you can read this more about this problem on this article, the whole idea will be using the traversal algorithm to implement a similar tool like the shown in that article.

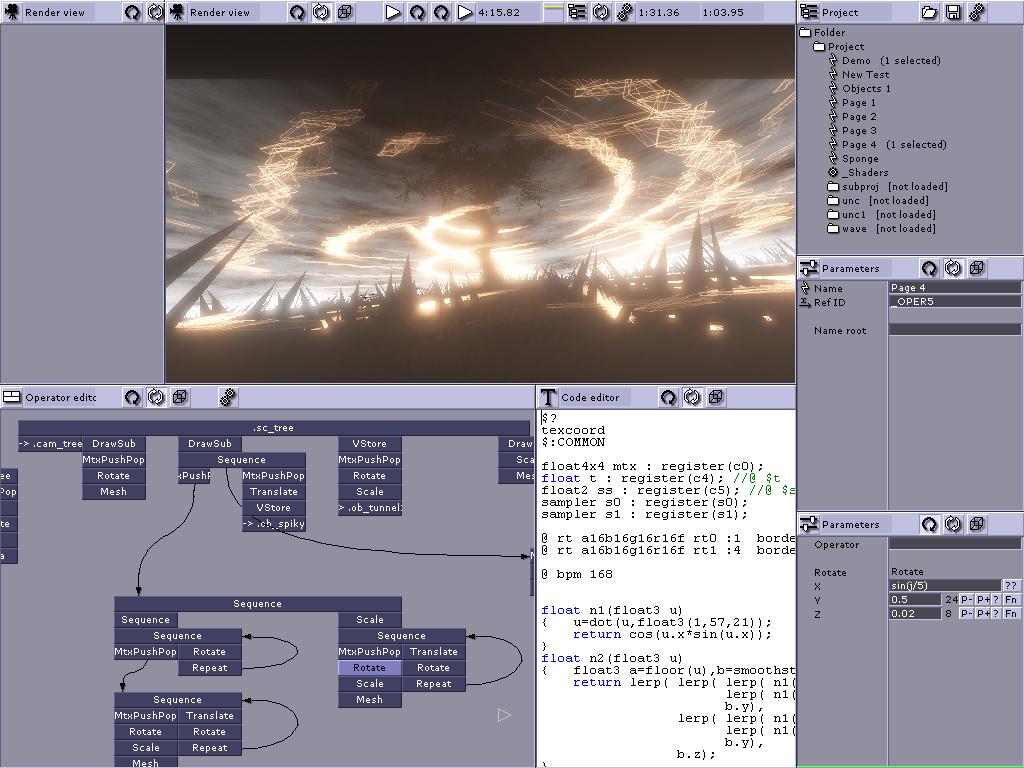
Here's a screenshot showing up the whole power of this type of data structure I want to figure out how to traverse&run:

Jehial

That a rendering engine you're working on? Looks quite good. – Bowser

@Bowser Agree, that's awesome! That rendering engine is not mine at all, I intend to create a similar tool to the ones I've referenced in my post! Here you can take a look to some of the amazing prods the author of such tool has been able to create. Of course, be aware of the size of those executables, no more than 4kb and 8kb, have fun ;-) – Jehial

So if I'm understanding your problem correctly, you're trying to create an algorithm that searches for something in a directed cyclic graph, using a depth-first algorithm. You would also prefer an iterative solution over a recursive one. Is that correct? – Amersham

What is the expected output for the first example you have given? Please just show the order of visiting the nodes, with the desired repeats. – Bowser

Do you just want to visit every node, or is the order in which order the nodes are visited? For example why would bfs not work for you? – Ceric

@Amersham It's not about searching but execution, you can see as a good example Evil Tak answer. About iterative over recursive, well, ideally I'd like it to be an elegant (short) solution which doesn't crash (Max recursion depth exceeded won't happen no matter which graph you create on the editor). When I said ideally the version would be iterative I meant the fact of max recursion depth execeeded basically but if the solution is much more elegant than the iterative, why not? – Jehial

@Ceric The children order will be always left to right. In case you're creating arrows from node, the point, from which arrow starts matters. Additionally, arrow can start on the sides of a block, in which case it can be very first (if it's on the left) or very last (on the right) node. – Jehial

@Bowser About the order of visiting the node with the desired repeats, I'll need to confirm your answer once I plug in your traversal algorithm on the editor. I'll be creating the editor this week and I'll be testing all possible solutions posted here. At the end of the week, once I've tested all of them I'll post the results I get in terms of performance and I'll judge which one deserves the bounty (performance+elegant). For your good effort, let's start giving you +1 – Jehial

Let's say you have the following graph a->b,c, b->c and c->d. Should the algorithm go through a->b->c->d and a->c->d or would you be satisfied with a->b->c->d and a->c (dfs would stop as c is already visited)? – Ceric

It's not clear what exactly you want MAX_THRESHOLD to do. If you don't expect that there will be any infinite cycles and you just want to avoid crashing if there is one, then you should use Brent's cycle finding algorithm, which is easily adapted to detect cycles in a DFS: en.wikipedia.org/wiki/Cycle_detection#Brent.27s_algorithm – Bankruptcy

Looks like a duplicate of #1321188 if it's only about traversal. Basically, you convert it to a tree by ignoring cycles as you see them, and every tree has an equivalent binary tree. As noted there, breadth-first search shall typically produce a more reasonably-looking tree. – Calvert

@Ceric Theorically in that case you'd have a_start, b_start, c_start, d_start, d_end, c_end, b_end, a_middle, c_start, d_start, d_end, c_end, a_end. C and D will be executed twice, which is exactly what we want here. – Jehial

@Jehial please let us (me) know when this tool of yours is finished. I'd love to take it for a spin and, if possible, even contribute to it! – Bowser

@Bowser Sure, it'll take me a while though. WIP after 3 coding sessions. Main goal of this project is not just having fun drawing cool stuff onto screen but learning about good software engineering practices. Before advancing any further I'm trying to get solved these set of questions {q1, q2, q3} – Jehial

Answer 1

Before I start, Run the code on CodeSkulptor! I also hope that the comments elaborate what I have done enough. If you need more explanation, look at my explanation of the recursive approach below the code.

# If you don't want global variables, remove the indentation procedures
indent = -1

MAX_THRESHOLD = 10
INF = 1 << 63

def whitespace():
    global indent
    return '|  ' * (indent)

class Node:
    def __init__(self, name, num_repeats=INF):
        self.name = name
        self.num_repeats = num_repeats

    def start(self):
        global indent
        if self.name.find('Sequence') != -1:
            print whitespace()
            indent += 1
        print whitespace() + '%s_start' % self.name

    def middle(self):
        print whitespace() + '%s_middle' % self.name

    def end(self):
        global indent
        print whitespace() + '%s_end' % self.name
        if self.name.find('Sequence') != -1:
            indent -= 1
            print whitespace()

def dfs(graph, start):
    visits = {}
    frontier = [] # The stack that keeps track of nodes to visit

    # Whenever we "visit" a node, increase its visit count
    frontier.append((start, start.num_repeats))
    visits[start] = visits.get(start, 0) + 1

    while frontier:
        # parent_repeat_count usually contains vertex.repeat_count
        # But, it may contain a higher value if a repeat node is its ancestor
        vertex, parent_repeat_count = frontier.pop()

        # Special case which signifies the end
        if parent_repeat_count == -1:
            vertex.end()
            # We're done with this vertex, clear visits so that 
            # if any other node calls us, we're still able to be called
            visits[vertex] = 0
            continue

        # Special case which signifies the middle
        if parent_repeat_count == -2:
            vertex.middle()
            continue  

        # Send the start message
        vertex.start()

        # Add the node's end state to the stack first
        # So that it is executed last
        frontier.append((vertex, -1))

        # No more children, continue
        # Because of the above line, the end method will
        # still be executed
        if vertex not in graph:
            continue

        ## Uncomment the following line if you want to go left to right neighbor
        #### graph[vertex].reverse()

        for i, neighbor in enumerate(graph[vertex]):
            # The repeat count should propagate amongst neighbors
            # That is if the parent had a higher repeat count, use that instead
            repeat_count = max(1, parent_repeat_count)
            if neighbor.num_repeats != INF:
                repeat_count = neighbor.num_repeats

            # We've gone through at least one neighbor node
            # Append this vertex's middle state to the stack
            if i >= 1:
                frontier.append((vertex, -2))

            # If we've not visited the neighbor more times than we have to, visit it
            if visits.get(neighbor, 0) < MAX_THRESHOLD and visits.get(neighbor, 0) < repeat_count:
                frontier.append((neighbor, repeat_count))
                visits[neighbor] = visits.get(neighbor, 0) + 1

def dfs_rec(graph, node, parent_repeat_count=INF, visits={}):
    visits[node] = visits.get(node, 0) + 1

    node.start()

    if node not in graph:
        node.end()
        return

    for i, neighbor in enumerate(graph[node][::-1]):
        repeat_count = max(1, parent_repeat_count)
        if neighbor.num_repeats != INF:
            repeat_count = neighbor.num_repeats

        if i >= 1:
            node.middle()

        if visits.get(neighbor, 0) < MAX_THRESHOLD and visits.get(neighbor, 0) < repeat_count:
            dfs_rec(graph, neighbor, repeat_count, visits)

    node.end()  
    visits[node] = 0

Sequence1 = Node('Sequence1')
MtxPushPop1 = Node('MtxPushPop1')
Rotate1 = Node('Rotate1')
Repeat1 = Node('Repeat1', 2)

Sequence2 = Node('Sequence2')
MtxPushPop2 = Node('MtxPushPop2')
Translate = Node('Translate')
Rotate2 = Node('Rotate2')
Rotate3 = Node('Rotate3')
Scale = Node('Scale')
Repeat2 = Node('Repeat2', 3)
Mesh = Node('Mesh')

cyclic_graph = {
        Sequence1: [MtxPushPop1, Rotate1],
        MtxPushPop1: [Sequence2],
        Rotate1: [Repeat1],
        Sequence2: [MtxPushPop2, Translate],
        Repeat1: [Sequence1],
        MtxPushPop2: [Rotate2],
        Translate: [Rotate3],
        Rotate2: [Scale],
        Rotate3: [Repeat2],
        Scale: [Mesh],
        Repeat2: [Sequence2]
    }

dfs(cyclic_graph, Sequence1)

print '-'*40

dfs_rec(cyclic_graph, Sequence1)

print '-'*40

dfs({Sequence1: [Translate], Translate: [Sequence1]}, Sequence1)

print '-'*40

dfs_rec({Sequence1: [Translate], Translate: [Sequence1]}, Sequence1)

The input and (well formatted and indented) output can be found here. If you want to see how I formatted the output, please refer to the code, which can also be found on CodeSkulptor.

---

Right, on to the explanation. The easier to understand but much more inefficient recursive solution, which I'll use to help explain, follows:

def dfs_rec(graph, node, parent_repeat_count=INF, visits={}):
    visits[node] = visits.get(node, 0) + 1

    node.start()

    if node not in graph:
        node.end()
        return

    for i, neighbor in enumerate(graph[node][::-1]):
        repeat_count = max(1, parent_repeat_count)
        if neighbor.num_repeats != INF:
            repeat_count = neighbor.num_repeats

        if i >= 1:
            node.middle()

        if visits.get(neighbor, 0) < MAX_THRESHOLD and visits.get(neighbor, 0) < repeat_count:
            dfs_rec(graph, neighbor, repeat_count, visits)

    node.end()  
    visits[node] = 0

1. The first thing we do is visit the node. We do this by incrementing the number of visits of the node in the dictionary.
2. We then raise the start event of the node.
3. We do a simple check to see if the node is a childless (leaf) node or not. If it is, we raise the end event and return.
4. Now that we've established that the node has neighbors, we iterate through each neighbor. Side Note: I reverse the neighbor list (by using graph[node][::-1]) in the recursive version to maintain the same order (right to left) of traversal of neighbors as in the iterative version.
   1. For each neighbor, we first calculate the repeat count. The repeat count propagates (is inherited) through from the ancestor nodes, so the inherited repeat count is used unless the neighbor contains a repeat count value.
   2. We raise the middle event of the current node (not the neighbor) if the second (or greater) neighbor is being processed.
   3. If the neighbor can be visited, the neighbor is visited. The visitability check is done by checking whether the neighbor has been visited less than a) MAX_THRESHOLD times (for pseudo-infinite cycles) and b) the above calculated repeat count times.
5. We're now done with this node; raise the end event and clear its visits in the hashtable. This is done so that if some other node calls it again, it does not fail the visitability check and/or execute for less than the required number of times.

Bowser

Could you please post the final version here in your answer instead CodeSkulptor? The one you pasted here is badly indented/formatted. And the one in CodeSkulptor isn't consider MAX_THRESHOLD so I don't know which one to evaluate. Btw, your version on CodeSkulptor is using global variables to deal with indentation and is not using the same classes I had used in my mcve (Node & NodeRepeat) – Jehial

@Jehial I can do that. Do you not want to use global variables? I mean, you won't be using that printing code in your editor, will you? – Bowser

Printing/Debugging code is a little nice/cool extra, that's why I haven't mentioned it as a requirement. I always prefer to avoid global variables in my code. Debugging the node execution will be handy to add some node profiling. Btw, my first version of the editor will be using python code to render the scene graph but probably in future versions I'll be using a c++ player, the editor will be able to create executables directly (but that's out of the question here). – Jehial

@Jehial makes sense. I'd avoid global variables too. Have you checked out the latest edits? They seem to do what you want. – Bowser

Yeah, I have checked them. The only minor details I find with your versions IMHO are the usage of this hacky line frontier.append((start, start.num_repeats if isinstance(start, NodeRepeat) else 2 << 31)) and the usage of global variables. For the rest, your algorithm seem is meeting requirements but I'll need to check it out graphically once I got the first draft of my editor running. Btw, your answer is looking nice! I'm sure if you edit&clean a bit and add its counterpart recursive version will help you get some good ammount of upvotes, you deserve it for the effort. – Jehial

@Jehial to be honest, that hacky line could have been avoided by using a single Node class (which I had done before), but you require two different classes for repeated Nodes. That line can definitely be beautified. I didn't use sys.maxint or maxsize since CodeSkulptor doesn't support it :P. The recursive solution should be much more trivial, will post it in a couple of hours. The only global variable I have used is the indent variable for the indented output, but that too can be refactored into a IndentedPrinter or similar. The special case hacks can also be removed but with more code. – Bowser

Mmmm, you're actually right, maybe it was my fault to tell you to stick to my mcve, that wasn't right, sorry about it. Let's not put any barrier from now on and let's try to find a simple elegant version of the algorithm without any constraints coming from my snippet – Jehial

@Jehial Improved my answer, and the code with a recursive solution + explanation. – Bowser

Answer 2

As per comment66244567 - reducing the graph to a tree by ignoring links to visited nodes and performing a breadth-first search, as this would produce a more natural-looking (and likely more balanced) tree:

def traverse(graph,node,process):
    seen={node}
    current_level=[node]
    while current_level:
        next_level=[]
        for node in current_level:
            process(node)
            for child in (link for link in graph.get(node,[]) if link not in seen):
                next_level.append(child)
                seen.add(child)
        current_level=next_level

With your graph and def process(node): print node, this produces:

In [24]: traverse(cyclic_graph,Sequence1,process)
Sequence1
MtxPushPop1
Rotate1
Sequence2
Repeat1
MtxPushPop2
Translate
Rotate2
Rotate3
Scale
Repeat2
Mesh

The other BFS algorithm, iterative deepening DFS (uses less memory at the cost of speed) isn't going to win you anything in this case: since you have to store references to visited nodes, you already consume O(n) memory. Neither you need to produce intermediate results (but you can anyway - e.g. yield something after processing a level).

Calvert

Thanks for your answer! But I don't see how your version is sticking to the requirements. For instance, where are start/middle/end methods going to be executed? – Jehial

The redefinition of __hash__() isn't required because that is the default definition. – Bowser

@Jehial they are supposed to be in process(). The question is about traversing the graph, and what you do with each node is irrelevant to that - so traversing is gonna be disjoint from processing and shall allow any processing rather than just what you gave as example. Writing the necessary process() is trivial, so I didn't clutter the answer with unnecessary details. – Calvert

@Calvert Alright, thanks for the answer in any case! Once I got the basics of my editor implemented this week I'll tweak & test your algorithm as well. Just let you know right now the best candidate for validation&bounties is Evil Tak's answer so far (in case you care about that :)) – Jehial

@Bowser thanks, I didn't know that (the docs only mention this indirectly). The default hash() for objects and instances is not its address itself though, it's _Py_HashPointer(<address>). – Calvert

SO answers are also supposed to be useful for future readers, not just one person, and irrelevant details are detrimental for that goal. – Calvert