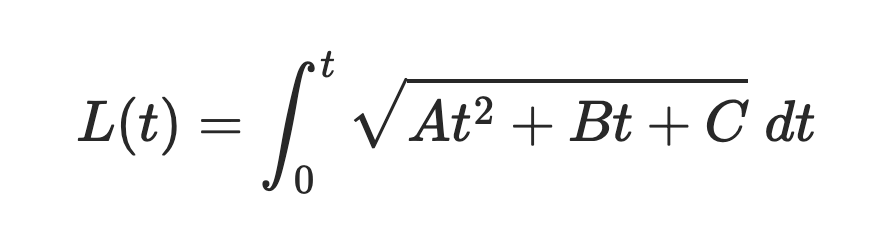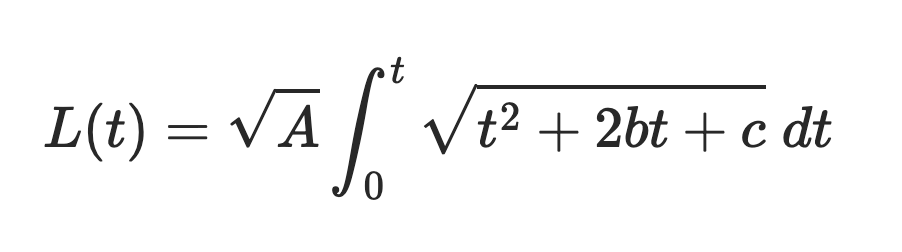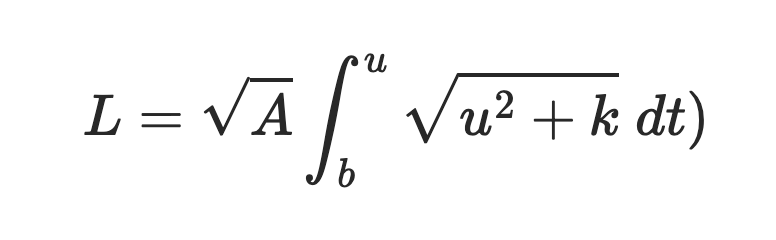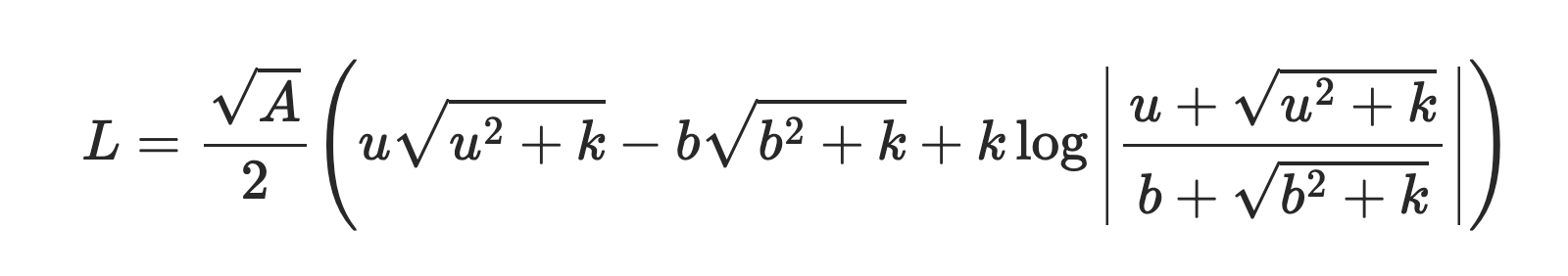Since I was sure a similar form solution would exist for that variable t case - I extended the solution given in the link.
Starting from the equation in the link:
![L(t)=\int_0^t\sqrt{At^2+Bt+C};dt]()
Which we can write as
![eL(t)=\sqrt{A}\int_0^t\sqrt{t^2+2bt+c};dt]()
Where b = B/(2A) and c = C/A.
Then transforming u = t + b we get
![L=\sqrt{A}\int_{b}^u\sqrt{u^2+k};dt)]()
Where k = c - b^2
Now we can use the integral identity from the link to obtain:
![L=\frac{\sqrt{A}}{2}\left(u\sqrt{u^2+k}-b\sqrt{b^2+k}+k\log\left|\frac{u+\sqrt{u^2+k}}{b+\sqrt{b^2+k}}\right|\right)]()
So, in summary, the required steps are:
- Calculate A,B,C as in the original equation.
- Calculate
b = B/(2A) and c = C/A
- Calculate
u = t + b and k = c -b^2
- Plug these values into the equation above.
[Edit by Spektre] I just managed to implement this in C++ so here the code (and working correctly matching naively obtained arc lengths):
float x0,x1,x2,y0,y1,y2; // control points of Bezier curve
float get_l_analytic(float t) // get arclength from parameter t=<0,1>
{
float ax,ay,bx,by,A,B,C,b,c,u,k,L;
ax=x0-x1-x1+x2;
ay=y0-y1-y1+y2;
bx=x1+x1-x0-x0;
by=y1+y1-y0-y0;
A=4.0*((ax*ax)+(ay*ay));
B=4.0*((ax*bx)+(ay*by));
C= (bx*bx)+(by*by);
b=B/(2.0*A);
c=C/A;
u=t+b;
k=c-(b*b);
L=0.5*sqrt(A)*
(
(u*sqrt((u*u)+k))
-(b*sqrt((b*b)+k))
+(k*log(fabs((u+sqrt((u*u)+k))/(b+sqrt((b*b)+k)))))
);
return L;
}
There is still room for improvement as some terms are computed more than once ...