Why does my water explode?

Question

I am trying to implement the Clavet method for simulating fluids in JavaScript, so debugging is a nightmare, which is why I'm asking here, hoping that someone who has gone through the same thing will tell me what I'm doing wrong.

I have it working OKAY so far:

But I have two problems:

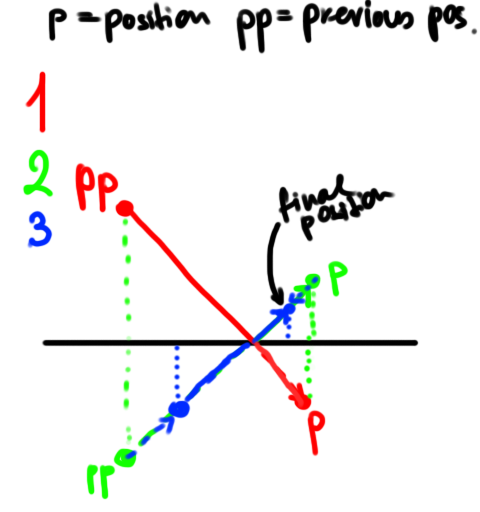
1) Since in this method everything is sort of "offset" by half a step, I'm not sure how to bounce the particles off the walls correctly. Right now I take the particle's position and previous position and flip them around the crossed wall, then scale around the crossing point by a bounce factor.

My logic tells me that this should work. The next step in the algorithm is to update particle velocities, so I reflect the previous position also. But in practice this gives me a result which I don't understand:

This shows the "forces" on the particles. The walls reflect way too much force, which keeps everything in perpetual motion.

Formula 4.58 in this paper apparently shows a way to prevent this, but I haven't been able to get it to work.

Also there's stuff in the paper I don't get, like what "we only want to reflect the velocity that was omitted in the collision" means. Why? Could someone ELI5 this stuff to me please?

2) Even when walls aren't involved, the simulation "explodes" periodically. This happens more with higher pressure:

This is JavaScript, so there's that, but I've gone over the code and there are no divisions by zero or situations where I can imagine a NaN happening.

I've seen some talk in the papers about sim instability, and I wonder if this is it. Most of what's in this literature is beyond me.

From what I did understand (I think), one of the ways to eliminate instability is viscosity, but I added it and it didn't help with the explosions:

I can post code, but at the get-it-to-work-first stage it's kind of hard to read right now.

One final question: how do I figure out how to convert from the pseudo constants in this method to physical units?

Edit: I've discovered that the sim freezes occasionally, it seems it does produce a NaN somewhere, but Chrome catches it way too late.

Prizewinner

as inspiration to others cut a gist with your code and we'll dig in gist.github.com – Dorthadorthea

gist.github.com/alexbourt/ca5b9e44f6ecbfcc6b8a52d805caa9f6 I warned you though. :) – Prizewinner

"everything in perpetual motion" isn't that real life? I'd have thought that to get stability you need dampening that reduces movement to zero once some minimum value is reached. While this is a very interesting demo, I don't think it's on topic here. If you have a specific programming issue, fine. But this seems much more about fluid dynamics algorithms in general. – Prudish

Sorry, I tried asking in the computer graphics forum, but I don't have enough reputation there to add all the pictures. :( Maybe a mod can move this question there? – Prizewinner

I'm interested in trying to see what's wrong, but I want to run your simulation, not just read it. The code you posted doesn't initialize itself and at least one function, getAngle, is missing. Could you post a complete example that can be pasted into a .html file and run in a browser? (Even putting it in a code block at the end of the question is fine.) – Tamer

My current progress is at bourt.com/particles.html. I added controls to play with parameters. Set the scale to 1 and go from there. Also, LMB moves particles, Ctrl+Shift+LMB adds some particles. (I haven't implemented any suggestions from the answers yet, though, as I was away.) – Prizewinner

Answer 1

assuming this is a cg project without rigorous physical significance...

first of all, you should really consider using a fixed time step for your simulation code, otherwise you'll get erratic (and visually disturbing) behaviour as dt ( and error ) jitters around. If you cannot get a consistent framerate as per your final requirements, positions should be interpolated rather than simulated at non fixed time points.

regarding your wall calculations, it clearly depends on the effect you want to ultimately achieve; so, if you apply a more or less momentum preserving mirror condition ( as you're doing now ) particles will continue 'circulating' around even if a damping is applied. If you want the fluid to 'stick' to the walls somehow, you need to introduce wall forces or some other stronger dissipative effect.

I ran your code, and after setting a consistent dt and tuning viscosity and simplifying the wall calculation to simpler "if (p.px < left) p.px = left + (left - p.px)*canvas.wallBounce; else if()..." conditions I get a nice 'relaxation' behaviour ( if this is what you're looking for ). Updating also the previous position is counterproductive as it will increase wall 'reflectiveness' so to speak.

Monaxial

Sorry for the dumb questions, I don't have a formal education in any of this, obviously. :) Do I understand correctly that the way I bounce the particles off the floor now, all the collective weight of the water is reflected back up, and that's why the bottom particles are so energetic? And if so, isn't that what happens in real life? – Prizewinner

if by "so energetic" you mean why the particles in your simulation appear more packed and faster near the walls, I think the reason is twofold: first, as pointed out by Davis Herring, the negative surface tension will increase their number density at the wall boundary and hence repel particles in the bulk ( this is why you see a 'gap' at the wall boundary ); second, as said above, unless you add wall forces, particles will tend to preserve their energy/momentum resulting in an always "swirling" lookiing kind of fluid ... this is further exacerbated due to time step jittering and numeric errors – Monaxial

regarding what happens in real life, this is not a trivial matter, even deciding what a "fluid element" really is requires non trivial knowledge on the subject ( fluid elements are not the fluid microscopic constituents, like molucules and such ... ). Anyway, real fluids ( superfluids excluded ) will sticks to walls at 'zero' distance ( and then either set into a stationary laminar motion or go into a separation flow followed by turbulent motion )... – Monaxial

at equilibrium, the only extra energy you should observe on your boundary particles should be surface tension and ( increasing towards the floor ) hydrostatic pressure due to gravity ... ( ignoring heat, etc... of course ) – Monaxial

I implemented all the suggestions in this thread and so far I have this: bourt.com/particles.html. I can get the crazy dancing forces to go away if I reduce the time step or rest density, but this doesn't seem to be that large a number of particles that I should have to do that... What am I missing? Is this an issue of rest density vs. cell size? Also, what's the simplest way math-wise to add heat (or something heat-like) to this? – Prizewinner

stackoverflow told me to avoid extended discussions in comments, ( I can move this into a chat though ) anyway, you can add a simplistic heat-like effect by adding a space varying rest density ... I don't understand the first part of your question ... – Monaxial

Let us continue this discussion in chat. – Prizewinner

Answer 2

Obviously there's a lot here. I'm sure I can't answer it all, but here are some hopefully significant points:

About the walls: what you've implemented is called a momentum mirror. In a fluid under pressure, the momentum mirror serves to attract particles with a sort of negative surface tension (because there are no particles beyond it to repel those near the boundary). The more tightly packed particles there will generate larger forces and be more likely to cause numerical problems (especially because their teleportation tends to grant them potential energy).

About the coefficient of restitution: the simple linear scaling around the collision produces a tangential force on impact which is not typical for momentum mirrors but does tend to produce a physically realistic no-slip condition.

About the second paper you linked: I think they're trying to do something intelligent based on their point projection. However, I don't know why they merely project back to the surface (rather than computing a time of collision and then a new position based on the (reduced) new velocity thereafter).

Phlebotomy