Find the area between two curves plotted in matplotlib (fill_between area)

Question

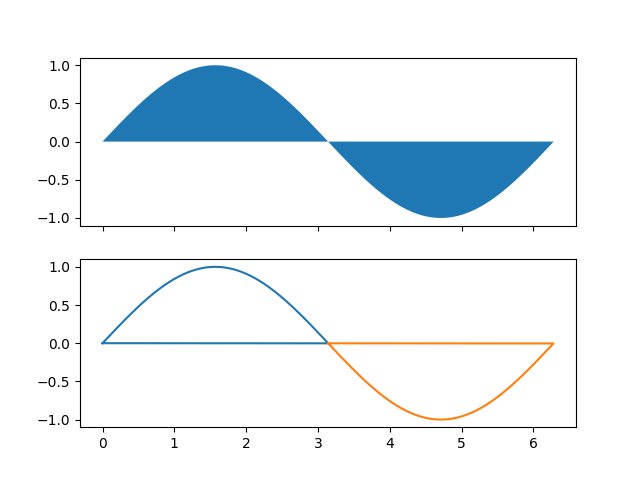
I have a list of x and y values for two curves, both having weird shapes, and I don't have a function for any of them. I need to do two things:

1. Plot it and shade the area between the curves like the image below.
2. Find the total area of this shaded region between the curves.

I'm able to plot and shade the area between those curves with fill_between and fill_betweenx in matplotlib, but I have no idea on how to calculate the exact area between them, specially because I don't have a function for any of those curves.
Any ideas?

I looked everywhere and can't find a simple solution for this. I'm quite desperate, so any help is much appreciated.

Thank you very much!

---

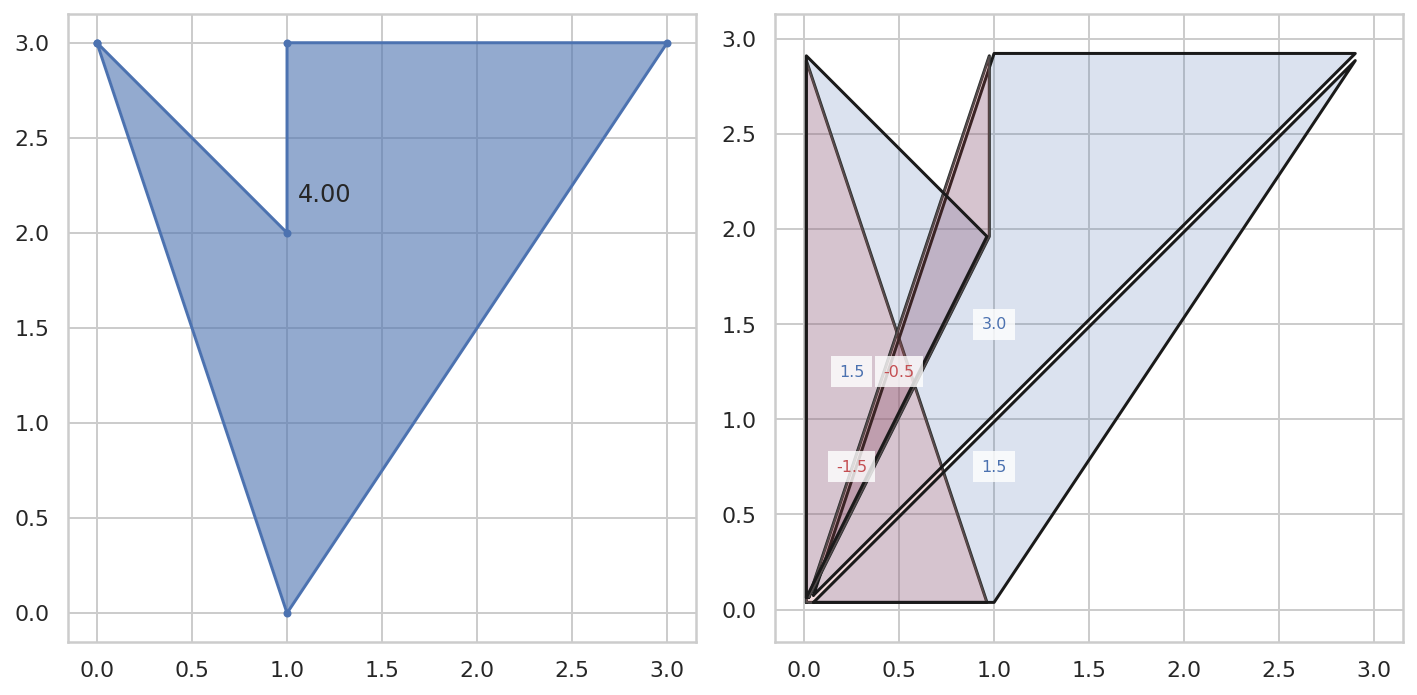
EDIT: For future reference (in case anyone runs into the same problem), here is how I've solved this: connected the first and last node/point of each curve together, resulting in a big weird-shaped polygon, then used shapely to calculate the polygon's area automatically, which is the exact area between the curves, no matter which way they go or how nonlinear they are. Works like a charm! :)

Here is my code:

from shapely.geometry import Polygon

x_y_curve1 = [(0.121,0.232),(2.898,4.554),(7.865,9.987)] #these are your points for curve 1 (I just put some random numbers)
x_y_curve2 = [(1.221,1.232),(3.898,5.554),(8.865,7.987)] #these are your points for curve 2 (I just put some random numbers)

polygon_points = [] #creates a empty list where we will append the points to create the polygon

for xyvalue in x_y_curve1:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 1

for xyvalue in x_y_curve2[::-1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 2 in the reverse order (from last point to first point)

for xyvalue in x_y_curve1[0:1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append the first point in curve 1 again, to it "closes" the polygon

polygon = Polygon(polygon_points)
area = polygon.area
print(area)

EDIT 2: Thank you for the answers. Like Kyle explained, this only works for positive values. If your curves go below 0 (which is not my case, as showed in the example chart), then you would have to work with absolute numbers.

Billiot

I really like that answer, but it should be noted that the area cancels above and below the first line. For example, consider a simple bowtie: coords = [(0,0),(0,1),(1,0),(1,1),(0,0)] Polygon(coords).area that gives an area of 0, although it isn't actually 0 – Misdemeanant

Instead, if you want the absolute value, to count both the positive and negative polygons, you should follow this answer (gis.stackexchange.com/a/243498), and then calculate the area of each polygon in the list. – Misdemeanant

Yes, i think the OP's method just subtracts one area from the other... This was the result which i got from the code. So Kyle's additions would be required. – Piecrust

Answer 1

The area calculation is straightforward in blocks where the two curves don't intersect: thats the trapezium as has been pointed out above. If they intersect, then you create two triangles between x[i] and x[i+1], and you should add the area of the two. If you want to do it directly, you should handle the two cases separately. Here's a basic working example to solve your problem. First, I will start with some fake data:

#!/usr/bin/python
import numpy as np

# let us generate fake test data
x = np.arange(10)
y1 = np.random.rand(10) * 20
y2 = np.random.rand(10) * 20

Now, the main code. Based on your plot, looks like you have y1 and y2 defined at the same X points. Then we define,

z = y1-y2
dx = x[1:] - x[:-1]
cross_test = np.sign(z[:-1] * z[1:])

cross_test will be negative whenever the two graphs cross. At these points, we want to calculate the x coordinate of the crossover. For simplicity, I will calculate x coordinates of the intersection of all segments of y. For places where the two curves don't intersect, they will be useless values, and we won't use them anywhere. This just keeps the code easier to understand.

Suppose you have z1 and z2 at x1 and x2, then we are solving for x0 such that z = 0:

# (z2 - z1)/(x2 - x1) = (z0 - z1) / (x0 - x1) = -z1/(x0 - x1)
# x0 = x1 - (x2 - x1) / (z2 - z1) * z1
x_intersect = x[:-1] - dx / (z[1:] - z[:-1]) * z[:-1]
dx_intersect = - dx / (z[1:] - z[:-1]) * z[:-1]

Where the curves don't intersect, area is simply given by:

areas_pos = abs(z[:-1] + z[1:]) * 0.5 * dx # signs of both z are same

Where they intersect, we add areas of both triangles:

areas_neg = 0.5 * dx_intersect * abs(z[:-1]) + 0.5 * (dx - dx_intersect) * abs(z[1:])

Now, the area in each block x[i] to x[i+1] is to be selected, for which I use np.where:

areas = np.where(cross_test < 0, areas_neg, areas_pos)
total_area = np.sum(areas)

That is your desired answer. As has been pointed out above, this will get more complicated if the both the y graphs were defined at different x points. If you want to test this, you can simply plot it (in my test case, y range will be -20 to 20)

negatives = np.where(cross_test < 0)
positives = np.where(cross_test >= 0)
plot(x, y1)
plot(x, y2)
plot(x, z)
plt.vlines(x_intersect[negatives], -20, 20)

Span

Answer 2

Define your two curves as functions f and g that are linear by segment, e.g. between x1 and x2, f(x) = f(x1) + ((x-x1)/(x2-x1))*(f(x2)-f(x1)). Define h(x)=abs(g(x)-f(x)). Then use scipy.integrate.quad to integrate h.

That way you don't need to bother about the intersections. It will do the "trapeze summing" suggested by ch41rmn automatically.

Imogen

@JulieD Is there a way to do this when you can't define your function but have a set of points instead? One of my functions is a line but the other is just points that I connect. Any ideas? – Koral

@Koral Yes, like in the OP's example, you can always define a function that is linear by segment between the points of a set, i.e. define a function that takes one x, finds the points (x1, x2) of the set that are just before and after it, and returns the f(x) above. – Imogen

Thanks for the response, I tried but can't get it to go. Can you provide an example? Maybe I could start a new question so you could answer that one and I can accept it that way. Let me know. Thanks. – Koral

@Koral If you open a new post where you show some attempt, yes, please do. – Imogen

Does a name of this procedure exist? Or do you now some mathematical references? – Idiolect

@Idiolect it is only the mathematical definition of a segment, then the difference ot two arbitrary functions. Also by its definition, h is the function that gives you the difference at any point x, so if you integrate it you get the area between the curves over the interval. Any math textbook has these, without a specific name (but extending it to N dimensions). – Imogen

Answer 3

Your set of data is quite "nice" in the sense that the two sets of data share the same set of x-coordinates. You can therefore calculate the area using a series of trapezoids.

e.g. define the two functions as f(x) and g(x), then, between any two consecutive points in x, you have four points of data:

(x1, f(x1))-->(x2, f(x2))
(x1, g(x1))-->(x2, g(x2))

Then, the area of the trapezoid is

A(x1-->x2) = ( f(x1)-g(x1) + f(x2)-g(x2) ) * (x2-x1)/2                         (1)

A complication arises that equation (1) only works for simply-connected regions, i.e. there must not be a cross-over within this region:

|\             |\/|
|_|     vs     |/\|

The area of the two sides of the intersection must be evaluated separately. You will need to go through your data to find all points of intersections, then insert their coordinates into your list of coordinates. The correct order of x must be maintained. Then, you can loop through your list of simply connected regions and obtain a sum of the area of trapezoids.

EDIT:

For curiosity's sake, if the x-coordinates for the two lists are different, you can instead construct triangles. e.g.

.____.
|   / \
|  /   \
| /     \
|/       \
._________.

Overlap between triangles must be avoided, so you will again need to find points of intersections and insert them into your ordered list. The lengths of each side of the triangle can be calculated using Pythagoras' formula, and the area of the triangles can be calculated using Heron's formula.

Cognate

Answer 4

I had the same problem.The answer below is based on an attempt by the question author. However, shapely will not directly give the area of the polygon in purple. You need to edit the code to break it up into its component polygons and then get the area of each. After-which you simply add them up.

Area Between two lines

Consider the lines below:

Sample Two lines If you run the code below you will get zero for area because it takes the clockwise and subtracts the anti clockwise area:

from shapely.geometry import Polygon

x_y_curve1 = [(1,1),(2,1),(3,3),(4,3)] #these are your points for curve 1 
x_y_curve2 = [(1,3),(2,3),(3,1),(4,1)] #these are your points for curve 2 

polygon_points = [] #creates a empty list where we will append the points to create the polygon

for xyvalue in x_y_curve1:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 1

for xyvalue in x_y_curve2[::-1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 2 in the reverse order (from last point to first point)

for xyvalue in x_y_curve1[0:1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append the first point in curve 1 again, to it "closes" the polygon

polygon = Polygon(polygon_points)
area = polygon.area
print(area)

The solution is therefore to split the polygon into smaller pieces based on where the lines intersect. Then use a for loop to add these up:

from shapely.geometry import Polygon

x_y_curve1 = [(1,1),(2,1),(3,3),(4,3)] #these are your points for curve 1 
x_y_curve2 = [(1,3),(2,3),(3,1),(4,1)] #these are your points for curve 2 

polygon_points = [] #creates a empty list where we will append the points to create the polygon

for xyvalue in x_y_curve1:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 1

for xyvalue in x_y_curve2[::-1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append all xy points for curve 2 in the reverse order (from last point to first point)

for xyvalue in x_y_curve1[0:1]:
    polygon_points.append([xyvalue[0],xyvalue[1]]) #append the first point in curve 1 again, to it "closes" the polygon

polygon = Polygon(polygon_points)
area = polygon.area

x,y = polygon.exterior.xy
    # original data
ls = LineString(np.c_[x, y])
    # closed, non-simple
lr = LineString(ls.coords[:] + ls.coords[0:1])
lr.is_simple  # False
mls = unary_union(lr)
mls.geom_type  # MultiLineString'

Area_cal =[]

for polygon in polygonize(mls):
    Area_cal.append(polygon.area)
    Area_poly = (np.asarray(Area_cal).sum())
print(Area_poly)

Testimonial

This is an interesting approach, but appears to need a few import lines: >>> from shapely.geometry import LineString; >>> from shapely.ops import unary_union; not sure about polygonize, perhaps from GDAL? – Belting

@Creek from shapely.ops import unary_union, polygonize – Piecrust

Answer 5

The area_between_two_curves function in pypi library similaritymeasures (released in 2018) might give you what you need. I tried a trivial example on my side, comparing the area between a function and a constant value and got pretty close tie-back to Excel (within 2%). Not sure why it doesn't give me 100% tie-back, maybe I am doing something wrong. Worth considering though.

Mayer

Answer 6

A straightforward application of the area of a general polygon (see Shoelace formula) makes for a super-simple and fast, vectorized calculation:

def area(p):
    # for p: 2D vertices of a polygon:
    # area = 1/2 abs(sum(p0 ^ p1 + p1 ^ p2 + ... + pn-1 ^ p0))
    # where ^ is the cross product
    return np.abs(np.cross(p, np.roll(p, 1, axis=0)).sum()) / 2

Application to area between two curves. In this example, we don't even have matching x coordinates!

np.random.seed(0)
n0 = 10
n1 = 15
xy0 = np.c_[np.linspace(0, 10, n0), np.random.uniform(0, 10, n0)]
xy1 = np.c_[np.linspace(0, 10, n1), np.random.uniform(0, 10, n1)]

p = np.r_[xy0, xy1[::-1]]
>>> area(p)
4.9786...

Plot:

plt.plot(*xy0.T, 'b-')
plt.plot(*xy1.T, 'r-')
p = np.r_[xy0, xy1[::-1]]
plt.fill(*p.T, alpha=.2)

Speed

For both curves having 1 million points:

n = 1_000_000
xy0 = np.c_[np.linspace(0, 10, n), np.random.uniform(0, 10, n)]
xy1 = np.c_[np.linspace(0, 10, n), np.random.uniform(0, 10, n)]

%timeit area(np.r_[xy0, xy1[::-1]])
# 42.9 ms ± 140 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Simple viz of polygon area calculation

# say:
p = np.array([[0, 3], [1, 0], [3, 3], [1, 3], [1, 2]])

p_closed = np.r_[p, p[:1]]
fig, axes = plt.subplots(ncols=2, figsize=(10, 5), subplot_kw=dict(box_aspect=1), sharex=True)
ax = axes[0]
ax.set_aspect('equal')
ax.plot(*p_closed.T, '.-')
ax.fill(*p_closed.T, alpha=0.6)
center = p.mean(0)
txtkwargs = dict(ha='center', va='center')
ax.text(*center, f'{area(p):.2f}', **txtkwargs)
ax = axes[1]
ax.set_aspect('equal')
for a, b in zip(p_closed, p_closed[1:]):
    ar = 1/2 * np.cross(a, b)
    pos = ar >= 0
    tri = np.c_[(0,0), a, b, (0,0)].T
    # shrink a bit to make individual triangles easier to visually identify
    center = tri.mean(0)
    tri = (tri - center)*0.95 + center
    c = 'b' if pos else 'r'
    ax.plot(*tri.T, 'k')
    ax.fill(*tri.T, c, alpha=0.2, zorder=2 - pos)
    t = ax.text(*center, f'{ar:.1f}', color=c, fontsize=8, **txtkwargs)
    t.set_bbox(dict(facecolor='white', alpha=0.8, edgecolor='none'))

plt.tight_layout()

Groping

Answer 7

None of the answers on this thread did what I wanted, so I merged a few different sources together. I was explicitly looking to get the positive area of two intersecting functions, and a lot of these approaches had issues with areas cancelling out. In this example, I am calculating the area between a sin curve and y = 0, which for one full period is 4.

Gist here: https://gist.github.com/amstrudy/0bddab089c7ee36ab49aec8d2363648d

import math
import numpy as np
import matplotlib.pyplot as plt

from shapely.geometry import Polygon, LineString
from shapely.ops import unary_union, polygonize

# I found it very challenging to find code online that properly finds the positive area between two curves.
# Here is an example that works: we want the area between a sin function and y = 0, which for one full period of a sin function is 4.
# This script calculates this area to be 3.994... close enough!
# In order to make this work, the script calculates the area of each separate polygon (created by the intersection of the two functions) separately.

x = np.arange(0, 4 * math.pi, 0.01)
y1 = np.sin(x)

fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)

pc = ax1.fill_between(x, 0, y1)

sum_area = 0

for path in pc.get_paths():
    for vertices in path.to_polygons():
        vertices_array = np.array(vertices)

        # Create a Shapely Polygon from the vertices
        polygon = Polygon(vertices_array)

        # original data
        ls = LineString(np.c_[x, y1])
        # closed, non-simple
        lr = LineString(ls.coords[:] + ls.coords[0:1])
        assert(lr.is_simple == False)
        
        # Create MultiLineString
        mls = unary_union(lr)
        
        # Sum over LineStrings in mls to get total area
        area_cal =[]

        for polygon in polygonize(mls):
            area_cal.append(polygon.area)
            area_poly = (np.asarray(area_cal).sum())
            x,y = polygon.exterior.xy
            ax2.plot(x,y)
            
        sum_area += area_poly

print(sum_area)

plt.show()

Sherasherar

Answer 8

An elegant way to do that is by combining the fill_between() function and the Polygon function in the shapely.geometry package. fill_between() returns a PolyCollection object, from which you can get the paths of each polygon. The good thing is you can even compute the area separately for y2>y1 and y2<y1.

import numpy as np
import matplotlib.pyplot as plt
from shapely.geometry import Polygon

n = 10
y1 = np.random.uniform(0, 10, n)
y2 = np.random.uniform(0, 10, n)

fig, ax = plt.subplots()
poly_collect = ax.fill_between(y1, y2)
paths = poly_collect.get_paths()
area = 0
for path in paths:
    poly = Polygon(path.vertices)
    area += poly.area

Resile