Comparing Results from StandardScaler vs Normalizer in Linear Regression

Question

I'm working through some examples of Linear Regression under different scenarios, comparing the results from using Normalizer and StandardScaler, and the results are puzzling.

I'm using the boston housing dataset, and prepping it this way:

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

#load the data
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df['PRICE'] = boston.target

I'm currently trying to reason about the results I get from the following scenarios:

• Initializing Linear Regression with the parameter normalize=True vs using Normalizer
• Initializing Linear Regression with the parameter fit_intercept = False with and without standardization.

Collectively, I find the results confusing.

Here's how I'm setting everything up:

# Prep the data
X = df.iloc[:, :-1]
y = df.iloc[:, -1:]
normal_X = Normalizer().fit_transform(X)
scaled_X = StandardScaler().fit_transform(X)

#now prepare some of the models
reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)
reg3 = LinearRegression().fit(normal_X, y)
reg4 = LinearRegression().fit(scaled_X, y)
reg5 = LinearRegression(fit_intercept=False).fit(scaled_X, y)

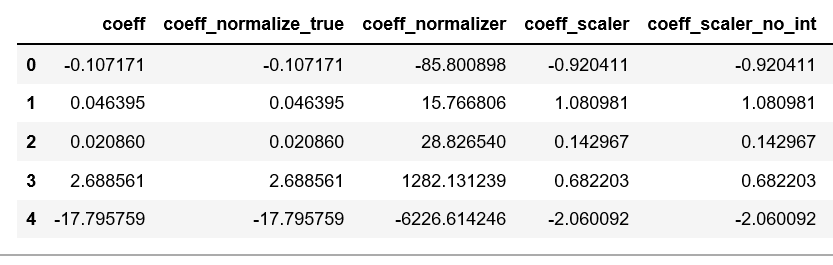
Then, I created 3 separate dataframes to compare the R_score, coefficient values, and predictions from each model.

To create the dataframe to compare coefficient values from each model, I did the following:

#Create a dataframe of the coefficients
coef = pd.DataFrame({
    'coeff':                       reg1.coef_[0],
    'coeff_normalize_true':        reg2.coef_[0],
    'coeff_normalizer':            reg3.coef_[0],
    'coeff_scaler':                reg4.coef_[0],
    'coeff_scaler_no_int':         reg5.coef_[0]
})

Here's how I created the dataframe to compare the R^2 values from each model:

scores = pd.DataFrame({
    'score':                        reg1.score(X, y),
    'score_normalize_true':         reg2.score(X, y),
    'score_normalizer':             reg3.score(normal_X, y),
    'score_scaler':                 reg4.score(scaled_X, y),
    'score_scaler_no_int':          reg5.score(scaled_X, y)
    }, index=range(1)
)

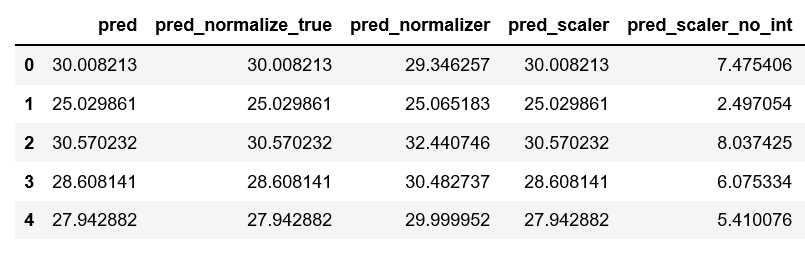
Lastly, here's the dataframe that compares the predictions from each:

predictions = pd.DataFrame({
    'pred':                        reg1.predict(X).ravel(),
    'pred_normalize_true':         reg2.predict(X).ravel(),
    'pred_normalizer':             reg3.predict(normal_X).ravel(),
    'pred_scaler':                 reg4.predict(scaled_X).ravel(),
    'pred_scaler_no_int':          reg5.predict(scaled_X).ravel()
}, index=range(len(y)))

Here are the resulting dataframes:

COEFFICIENTS:

SCORES:

PREDICTIONS:

I have three questions that I can't reconcile:

1. Why is there absolutely no difference between the first two models? It appears that setting normalize=False does nothing. I can understand having predictions and R^2 values that are the same, but my features have different numerical scales, so I'm not sure why normalizing would have no effect at all. This is doubly confusing when you consider that using StandardScaler changes the coefficients considerably.
2. I don't understand why the model using Normalizer causes such radically different coefficient values from the others, especially when the model with LinearRegression(normalize=True) makes no change at all.

If you were to look at the documentation for each, it appears they're very similar if not identical.

From the docs on sklearn.linear_model.LinearRegression():

normalize : boolean, optional, default False

This parameter is ignored when fit_intercept is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm.

Meanwhile, the docs on sklearn.preprocessing.Normalizer states that it normalizes to the l2 norm by default.

I don't see a difference between what these two options do, and I don't see why one would have such radical differences in coefficient values from the other.

3. The results from the model using the StandardScaler are coherent to me, but I don't understand why the model using StandardScaler and setting set_intercept=False performs so poorly.

From the docs on the Linear Regression module:

fit_intercept : boolean, optional, default True

whether to calculate the intercept for this model. If set to False, no
intercept will be used in calculations (e.g. data is expected to be already
centered).

The StandardScaler centers your data, so I don't understand why using it with fit_intercept=False produces incoherent results.

Crescentic

Answer 1

1. The reason for no difference in co-efficients between the first two models is that Sklearn de-normalize the co-efficients behind the scenes after calculating the co-effs from normalized input data. Reference

This de-normalization has been done because for test data, we can directly apply the co-effs. and get the prediction without normalizing the test data.

Hence, setting normalize=True do have impact on co-efficients but they dont affect the best fit line anyway.

2. Normalizer does the normalization with respect to each sample (meaning row-wise). You see the reference code here.

From documentation:

Normalize samples individually to unit norm.

whereas normalize=True does the normalization with respect to each column/ feature. Reference

Example to understand the impact of normalization at different dimension of the data. Let us take two dimensions x1 & x2 and y be the target variable. Target variable value is color coded in the figure.

import matplotlib.pyplot as plt
from sklearn.preprocessing import Normalizer,StandardScaler
from sklearn.preprocessing.data import normalize

n=50
x1 = np.random.normal(0, 2, size=n)
x2 = np.random.normal(0, 2, size=n)
noise = np.random.normal(0, 1, size=n)
y = 5 + 0.5*x1 + 2.5*x2 + noise

fig,ax=plt.subplots(1,4,figsize=(20,6))

ax[0].scatter(x1,x2,c=y)
ax[0].set_title('raw_data',size=15)

X = np.column_stack((x1,x2))

column_normalized=normalize(X, axis=0)
ax[1].scatter(column_normalized[:,0],column_normalized[:,1],c=y)
ax[1].set_title('column_normalized data',size=15)

row_normalized=Normalizer().fit_transform(X)
ax[2].scatter(row_normalized[:,0],row_normalized[:,1],c=y)
ax[2].set_title('row_normalized data',size=15)

standardized_data=StandardScaler().fit_transform(X)
ax[3].scatter(standardized_data[:,0],standardized_data[:,1],c=y)
ax[3].set_title('standardized data',size=15)

plt.subplots_adjust(left=0.3, bottom=None, right=0.9, top=None, wspace=0.3, hspace=None)
plt.show()

You could see that best fit line for data in fig 1,2 and 4 would be the same; signifies that the R2_-score will not change due to column/feature normalization or standardizing data. Just that, it ends up with different co-effs. values.

Note: best fit line for fig3 would be different.

3. When you set the fit_intercept=False, bias term is subtracted from the prediction. Meaning the intercept is set to zero, which otherwise would have been mean of target variable.

The prediction with intercept as zero would be expected to perform bad for problems where target variables are not scaled (mean =0). You can see a difference of 22.532 in every row, which signifies the impact of the output.

Peritonitis

When you @Peritonitis put "This de-normalization has been done so that any test data, we can directly apply the co-effs. and get the prediction with normalizing the test data." do you really mean "without normalizing the test data"? – Koah

ya, you are right, I meant without normalising the test data. – Peritonitis

@Peritonitis We are told not to select predictors based on regular regression coef's. We are told to use standardized regression coef's to select predictors. Is that the purpose of this code bock std = StandardScaler() std.fit(X.values) X_tr = std.transform(X.values)? After this we can then safely run a lasso model and use the coef's to select predictors? – Babi

Yes you’re right – Peritonitis

Answer 2

Answer to Q1

I am assuming that what you mean with the first 2 models is reg1 and reg2. Let us know if that is not the case.

A linear regression has the same predictive power if you normalize the data or not. Therefore, using normalize=True has no impact on the predictions. One way to understand this is to see that normalization (column-wise) is a linear operation on each of the columns ((x-a)/b) and linear transformations of the data on a Linear regression does not affect coefficient estimation, only change their values. Notice that this statement is not true for Lasso/Ridge/ElasticNet.

So, why aren't the coefficients different? Well, normalize=True also takes into account that what the user normally wants is the coefficients on the original features, not the normalised features. As such, it adjusts the coefficients. One way to check that this makes sense is to use a simpler example:

# two features, normal distributed with sigma=10
x1 = np.random.normal(0, 10, size=100)
x2 = np.random.normal(0, 10, size=100)

# y is related to each of them plus some noise
y = 3 + 2*x1 + 1*x2 + np.random.normal(0, 1, size=100)

X = np.array([x1, x2]).T  # X has two columns

reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)

# check that coefficients are the same and equal to [2,1]
np.testing.assert_allclose(reg1.coef_, reg2.coef_) 
np.testing.assert_allclose(reg1.coef_, np.array([2, 1]), rtol=0.01)

Which confirms that both methods correctly capture the real signal between [x1,x2] and y, namely, the 2 and 1 respectively.

Answer to Q2

Normalizer is not what you would expect. It normalises each row row-wise. So, the results will change dramatically, and likely destroy relationship between features and the target that you want to avoid except for specific cases (e.g. TF-IDF).

To see how, assume the example above, but consider a different feature, x3, that is not related with y. Using Normalizer causes x1 to be modifed by the value of x3, decreasing the strenght of its relationship with y.

Discrepancy of coefficients between models (1,2) and (4,5)

The discrepancy between the coefficients is that when you standardise before fitting, the coefficients will be with respect to the standardised features, the same coefficients I referred in the first part of the answer. They can be mapped to the original parameters using reg4.coef_ / scaler.scale_:

x1 = np.random.normal(0, 10, size=100)
x2 = np.random.normal(0, 10, size=100)
y = 3 + 2*x1 + 1*x2 + np.random.normal(0, 1, size=100)
X = np.array([x1, x2]).T

reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)
scaler = StandardScaler()
reg4 = LinearRegression().fit(scaler.fit_transform(X), y)

np.testing.assert_allclose(reg1.coef_, reg2.coef_) 
np.testing.assert_allclose(reg1.coef_, np.array([2, 1]), rtol=0.01)

# here
coefficients = reg4.coef_ / scaler.scale_
np.testing.assert_allclose(coefficients, np.array([2, 1]), rtol=0.01)

This is because, mathematically, setting z = (x - mu)/sigma, the model reg4 is solving y = a1*z1 + a2*z2 + a0. We can recover the relationship between y and x through simple algebra: y = a1*[(x1 - mu1)/sigma1] + a2*[(x2 - mu2)/sigma2] + a0, which can be simplified to y = (a1/sigma1)*x1 + (a2/sigma2)*x2 + (a0 - a1*mu1/sigma1 - a2*mu2/sigma2).

reg4.coef_ / scaler.scale_ represents [a1/sigma1, a2/sigma2] in the above notation, which is exactly what normalize=True does to guarantee that the coefficients are the same.

Descrepancy of score of model 5.

Standardized features are zero mean, but the target variable is not necessarily. Therefore, not fiting the intercept causes the model to disregard the mean of the target. In the example that I have been using, the "3" in y = 3 + ... is not fitted, which naturally decreases the predictive power of the model. :)

Sectary

Answer 3

The last question (3) about the incoherent results with fit_intercept=0 and standardized data has not been answered fully.

The OP is likely expecting StandardScaler to standardize X and y, which would make the intercept necessarily 0 (proof 1/3 of the way down).

However StandardScaler ignores y. see the api.

TransformedTargetRegressor offers a solution. This approach is also useful for non-linear transformations of the dependent variable such as the log transformation of y (but consider this).

Here's an example that resolves OP's issue #3:

from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import make_pipeline
from sklearn.datasets import make_regression
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
import numpy as np

# define a custom transformer
class stdY(BaseEstimator,TransformerMixin):
    def __init__(self):
        pass
    def fit(self,Y):
        self.std_err_=np.std(Y)
        self.mean_=np.mean(Y)
        return self
    def transform(self,Y):
        return (Y-self.mean_)/self.std_err_
    def inverse_transform(self,Y):
        return Y*self.std_err_+self.mean_

# standardize X and no intercept pipeline
no_int_pipe=make_pipeline(StandardScaler(),LinearRegression(fit_intercept=0)) # only standardizing X, so not expecting a great fit by itself.

# standardize y pipeline
std_lin_reg=TransformedTargetRegressor(regressor=no_int_pipe, transformer=stdY()) # transforms y, estimates the model, then reverses the transformation for evaluating loss.

#after returning to re-read my answer, there's an even easier solution, use StandardScaler as the transfromer:
std_lin_reg_easy=TransformedTargetRegressor(regressor=no_int_pipe, transformer=StandardScaler())

# generate some simple data
X, y, w = make_regression(n_samples=100,
                          n_features=3, # x variables generated and returned 
                          n_informative=3, # x variables included in the actual model of y
                          effective_rank=3, # make less than n_informative for multicollinearity
                          coef=True,
                          noise=0.1,
                          random_state=0,
                          bias=10)

std_lin_reg.fit(X,y)
print('custom transformer on y and no intercept r2_score: ',std_lin_reg.score(X,y))

std_lin_reg_easy.fit(X,y)
print('standard scaler on y and no intercept r2_score: ',std_lin_reg_easy.score(X,y))

no_int_pipe.fit(X,y)
print('\nonly standard scalar and no intercept r2_score: ',no_int_pipe.score(X,y))

which returns

custom transformer on y and no intercept r2_score:  0.9999343800041816

standard scaler on y and no intercept r2_score:  0.9999343800041816

only standard scalar and no intercept r2_score:  0.3319175799267782

Nitrate