How to find convex hull in a 3 dimensional space

Question

Given a set of points S (x, y, z). How to find the convex hull of those points ?

I tried understanding the algorithm from here, but could not get much.

It says:

First project all of the points onto the xy-plane, and find an edge that is definitely on the hull by selecting the point with highest y-coordinate and then doing one iteration of gift wrapping to determine the other endpoint of the edge. This is the first part of the incomplete hull. We then build the hull iteratively. Consider this first edge; now find another point in order to form the first triangular face of the hull. We do this by picking the point such that all the other points lie to the right of this triangle, when viewed appropriately (just as in the gift-wrapping algorithm, in which we picked an edge such that all other points lay to the right of that edge). Now there are three edges in the hull; to continue, we pick one of them arbitrarily, and again scan through all the points to find another point to build a new triangle with this edge, and repeat this until there are no edges left. (When we create a new triangular face, we add two edges to the pool; however, we have to first check if they have already been added to the hull, in which case we ignore them.) There are O(n) faces, and each iteration takes O(n) time since we must scan all of the remaining points, giving O(n2).

Can anyone explain it in a more clearer way or suggest a simpler alternative approach.

Spiegel

Answer 1

Implementing the 3D convex hull is not easy, but many algorithms have been implemented, and code is widely available. At the high end of quality and time investment to use is CGAL. At the lower end on both measures is my own C code:
     
In between there is code all over the web, including this implementation of QuickHull.

Lubricant

"This implementation of QuickHull" site seems to have disappeared. Archive here: web.archive.org/web/20180106161310/http://thomasdiewald.com/… – Excoriate

This is a link-only answer, unfortunately. – Sexlimited

Answer 2

I would suggest first try an easier approach like quick hull. (Btw, the order for gift wrapping is O(nh) not O(n2), where h is points on hull and order of quick hull is O(n log n)).

Under average circumstances quick hull works quite well, but processing usually becomes slow in cases of high symmetry or points lying on the circumference of a circle. Quick hull can be broken down to the following steps:

1. Find the points with minimum and maximum x coordinates, those are bound to be part of the convex.

2. Use the line formed by the two points to divide the set in two subsets of points, which will be processed recursively.

3. Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.

4. The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.

5. Repeat the previous two steps on the two lines formed by the triangle (not the initial line).

6. Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

See this impementaion and explanation for 3d convex hull using quick hull algorithm.

Gift wrapping algorithm:

Jarvis's match algorithm is like wrapping a piece of string around the points. It starts by computing the leftmost point l, since we know that the left most point must be a convex hull vertex.This process will take linear time.Then the algorithm does a series of pivoting steps to find each successive convex hull vertex untill the next vertex is the original leftmost point again.

The algorithm find the successive convex hull vertex like this: the vertex immediately following a point p is the point that appears to be furthest to the right to someone standing at p and looking at the other points. In other words, if q is the vertex following p, and r is any other input point, then the triple p, q, r is in counter-clockwise order. We can find each successive vertex in linear time by performing a series of O(n) counter-clockwise tests.

Since the algorithm spends O(n) time for each convex hull vertex, the worst-case running time is O(n2). However, if the convex hull has very few vertices, Jarvis's march is extremely fast. A better way to write the running time is O(nh), where h is the number of convex hull vertices. In the worst case, h = n, and we get our old O(n2) time bound, but in the best case h = 3, and the algorithm only needs O(n) time. This is a so called output-sensitive algorithm, the smaller the output, the faster the algorithm.

The following image should give you more idea

Doorpost

It seems the OP is seeking help for 3D hulls, but your (nice!) descriptions are for 2D hulls... – Earring

Well if you understand 2d, 3d is a very simple generalization ;) – Doorpost

;) Having implemented both, I would judge them to be ... well, in different dimensions! :-) – Earring

Answer 3

GPL C++ code for finding 3D convex hulls is available at http://www.newtonapples.net/code/NewtonAppleWrapper_11Feb2016.tar.gz and a description of the O(n log(n)) algorithm at http://www.newtonapples.net/NewtonAppleWrapper.html

Rupe

Answer 4

One of the simplest algorithms for convex hull computation in 3D was presented in the paper The QuickHull algorithm for Convex Hulls by Barber, etc from 1995. Unfortunately the original paper lacks any figures to simplify its understanding.

The algorithm works iteratively by storing boundary faces of some convex set with the vertices from the subset of original points. The remaining points are divided on the ones already inside the current convex set and the points outside it. And each step consists in enlarging the convex set by including one of outside points in it until no one remains.

The authors propose to start the algorithm in 3D from any tetrahedron with 4 vertices in original points. If these vertices are selected so that they are on the boundary of convex hull then it will accelerate the algorithm (they will not be removed from boundary during the following steps). Also the algorithm can start from the boundary surface containing just 2 oppositely oriented triangles with 3 vertices in original points. Such points can be selected as follows.

1. The first point has with the minimal (x,y,z) coordinates, if compare coordinates lexicographically.
2. The second point is the most distant from the first one.
3. The third point is the most distant from the line through the first two points.

The next figure presents initial points and the starting 2 oppositely oriented triangles: The remaining points are subdivided in two sets:

1. Black points - above the plane containing the triangles - are associated with the triangle having normal oriented upward.
2. Red points - below the plane containing the triangles - are associated with the triangle having normal oriented downward.

On the following steps, the algorithm always associates each point currently outside the convex set with one of the boundary triangles that is "visible" from the point (point is within positive half-space of that triangle). More precisely each outside point is associated with the triangle, for which the distance between the point and the plane containing the triangle is the largest.

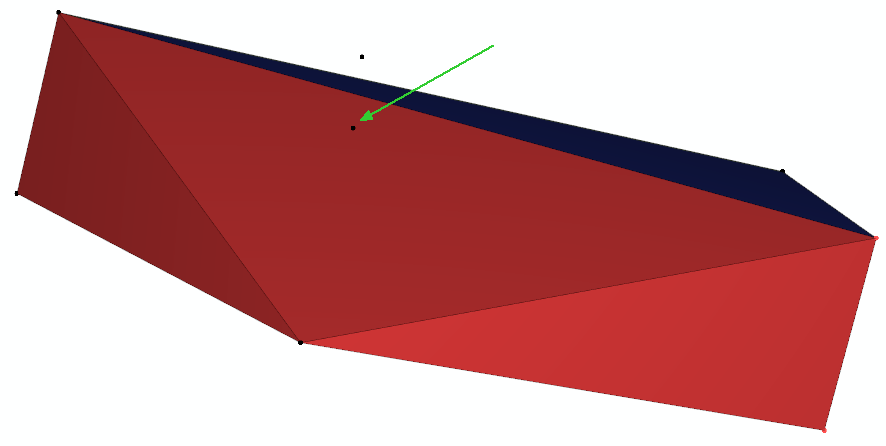
On each step of algorithm the furthest outside point is selected, then all faces of the current convex set visible from it are identified, these faces are removed from the convex set and replaced with the triangles having one vertex in furthest point and two other points on the horizon ridge (boundary of removed visible faces).

On the next figure the furthest point is pointed by green arrow and three visible triangles are highlighted in red:

Visible triangles deleted, back faces and inside points can be seen in the hole, horizon ridge is shown with red color:

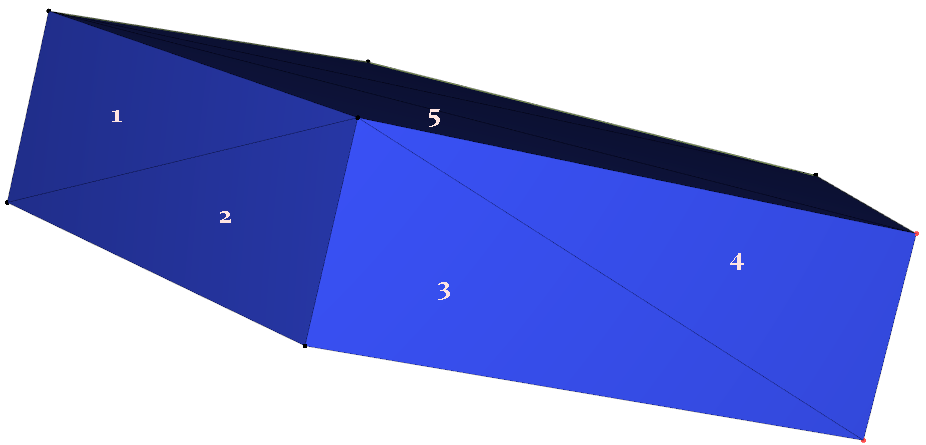
5 new triangles (joining at the added point) patch the hole in the surface:

The points previously associated with the removed triangles are either become inner for the updated convex set or redistributed among new triangles.

The last figure also presents the final result of convex hull computation without any remaining outside points. (The figures were prepared in MeshInspector application, having this algorithm implemented.)

Sexlimited