What is the difference between afferent couplings and efferent couplings of a class?

Question

Code quality metric tool like Sonar does provide the ability to drill down to a class and find out the number of:

1. Afferent (incoming) couplings
2. Efferent (outgoing) couplings

What are these two parameters? Can you please describe with a simple contrived example?

Cubiform

which programing language you are using? I am specific to PHP, there is a tool PHPMetrics, which can provide you a nice diagram and describe dependencies, add the same in Jenkins (if you are using at all) – Lapith

Answer 1

According to wikipedia:

Afferent Couplings (Ca): The number of classes in other packages that depend upon classes within the package is an indicator of the package's responsibility. Afferent = incoming.

Efferent Couplings (Ce): The number of classes in other packages that the classes in the package depend upon is an indicator of the package's dependence on externalities. Efferent = outgoing.

So, if you have classes (or packages or whatever) with the following structure:

class Foo {
    Quux q;
}

class Bar {
    Quux q;
}

class Quux {
    // ...
}

Then Foo and Bar each have one efferent coupling, and Quux has two afferent couplings.

Grisly

is Afferent coupling a better indicator of single responsibility principle being practiced? – Tolbooth

@Tolbooth - I'm not the best architect, but I don't think it indicates much. A class with too many afferent couplings could be used a lot because it does too much. Or it could just be handling some sort of crosscutting concern - logging, ORM unit of work, things like that. – Grisly

Answer 2

Since you mentioned Sonar, here is the definition provided by their documentation page

• Afferent couplings : A class afferent couplings is a measure of how many other classes use the specific class.
• Efferent couplings : A class efferent couplings is a measure of how many different classes are used by the specific class.

Hulburt

would object composition mean efferent coupling then? – Tolbooth

Answer 3

Coupling is a measure of dependencies.

Afferent Coupling :

• Who depends on you.
• Measure of how many other packages use a specific package.
• Incoming dependencies.

Efferent Coupling :

• Who do you depend on.
• Measure of how many different packages are used by a specific package.
• Outgoing dependencies.

Lapith

classes*, not packages – Tussock

Answer 4

In the booke fundamentals of software architecture these two concepts are used to calculate the instability of a class or package. The formula ce/ce+ca will give you the insrability (buginess factor).

Attila

Answer 5

Other users have already given answers from the definition perspective. Here, I have given an example of Afferent Coupling (Ca) and Efferent Coupling (Ce) for package-level granularity.

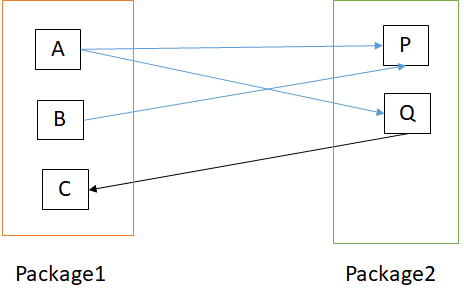
Suppose, package1 has 3 classes (i.e., A, B, C) and package2 has 2 classes (i.e., P, Q). For package1, class A has 2 out-going edges, class B has 1 out-going edge, and class C has 1 in-coming edge. Similarly, for package2, class P has 2 in-coming edges, and class Q has 1 in-coming and 1 out-going edge. [see the figure].

To calculate the Ca for a package, count the number of classes out of the package that has dependencies on it. You can proceed one by one for all classes of that package and then, take the union of dependent classes.

To calculate the Ce for a package, count the number of classes dependent on other packages inside the analyzed package. Count for all classes of that package and then, take the union.

So, the calculation will be as follows--

package1

Ca = {} union {} union {Q}  
   = {Q} 
   =  1

Ce = {P, Q} union {P} union {}
   = {P, Q,}
   = 2

package2

Ca = {A, B} union {A}
   = {A, B}
   = 2

Ce = {} union {C}
   = {C}
   = 1

Afferent Coupling and Efferent Coupling are used to calculate the Instability (I) of a package also. Instability is the ratio between Efferent Coupling (Ce) and the total package coupling (Ce + Ca). The formula is

I = Ce / (Ce + Ca)

The value of instability is between 0 to 1. The value towards 1 means unstable package (i.e., prone to change) and the value towards 0 means stable package.

For this example, Instability for package1 = 2/(1+2) = 0.67 and,

Instability for package2 = 1/(2+1) = 0.33

So, we can conclude that package1 is more unstable than package2 by measuring the afferent and efferent coupling.

For additional info you may check this paper also.

Mallemuck