I tried the following :
1) DFS, keeping track of level of each vertex in my DFS tree
2) Each time a back edge (x,y) is seen, I calculate cycle length = level[x] - level[y] + 1, and save it if it is smaller than the shortest
Can someone tell a counter example for which this approach is wrong ?
What could be a better way to find shortest cycle in undirected graphs ?
Thanks.
You cannot use DFS to find a shortest circle. We can easily create a counter example, where DFS leads finds only the longest circle. Lets have a look at the following graph:
As you can see we have nine nodes. If we start at the leftmost node A, the following DFS level could be possible:
We have two back edges while iterating:
(B , A), therefore we found a circle with length 8(D , A), therefore we found a circle with length 8However, the shortest circle has length 5. It's shown in blue in the next picture, whereas one of the previously found circles is shown in red:
You didn't see the blue circle because your DFS path doesn't contain it. Dagupa et al also mention this behaviour in their book:
But it also means that DFS can end up taking a long and convoluted route to a vertex that is actually very close by.
Well, that's not entirely true, one can use BFS (see next subsection), but you cannot use your formula. Take the following graph:
No fancy picture for this graph yet.
Every "o" is a node.
o---o
| |
+-------o---o-------+
| |
o----o----o----o----o
Lets see what levels are possible in BFS. If I start at the node in the middle, I get the following levels:
5~~~5 ~~~ are back-edges
| |
+-------4~~~4-------+
| |
3----2----1----2----3
And if I start at the left node, I get the following levels:
3~~~4
| |
+-------2---3-------+
| |
1----2----3----4~~~~4
Therefore, you cannot use your level formula.
Although not efficient, using an all-pair shortest path algorithm and checking the distance (i,i) for every node is a valid solution.
back edge term in the "fix for BFS" section, they shouldn't exist in a BFS traversal. –
Lys I think this is what you are looking for : https://web.archive.org/web/20170829175217/http://webcourse.cs.technion.ac.il/234247/Winter2003-2004/ho/WCFiles/Girth.pdf
You make a BFS from each node, thus you have complexity O(V*E)
D(x) + D(y) + 1 is right because x,y level difference is at most 1 when using BFS which implies the paths corresponding to x,y has no overlap, so root-...-x-y-...-root is one circuit. –
Prizewinner x,y in the left and right child tree of the root in one balanced tree, then "if we reach an already-explored vertex at depth r, then G must contain a cycle of size <= r" seems to be wrong. Because here D(y)=r and possibly D(x)=D(y), then D(x) + D(y) + 1<=r is impossible. Can someone solve with this problem? –
Prizewinner Let's say we've the graph with following edges,
1<->4, 4<->2, 4<->3, 2<->3, 3<->1
Then cycle 1, 4, 2, 3, 1 could be traversed before 1, 4, 3, 1 and as we are considering DFS, no node will be visited twice. So if 1, 4, 2, 3, 1 is traversed first, no chance that 1, 4, 3, 1 or 4, 2, 3, 3 will be traversed at all. So with DFS it can NOT be assured that we will get the shortest cycle always.
Possible Improvement: A BFS tree should work fine as it goes level by level and for BFS tree distance from root to any node is fixed, no matter in which order nodes are picked. Runtime: O(V+E) while modified Floyd-Warshall's algorithm would run in O(V^3) in worst case.
I'd like to explain an O(V * (V + E)) solution to this problem, which on sparse graphs is significantly more efficient than O(V^3) Floyd-Warshall.
First, let's fix the starting node of the cycle to be node S. Then, let's compute
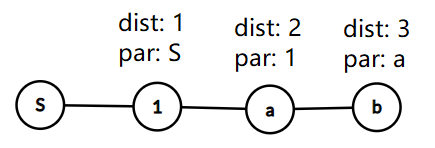
dist[i] = the shortest distance from node S to node i
par[i] = the parent of node i; any node j where dist[i] = dist[j] + 1
in O(V + E) time using a simple BFS.
Now, the key idea is to find, for each edge, the shortest cycle from S that passes through that edge. Then, because any cycle must pass through some edge of the graph, the shortest of all shortest cycles that pass through a given edge will yield the shortest cycle starting at S.
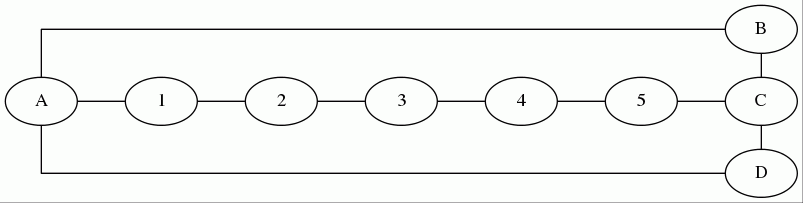
But how do we find the shortest cycle from S that passes through a given undirected edge (a, b)? The shortest length is NOT just dist[a] + dist[b] + 1 (from the cycle S -> a -> b -> S), because the paths S -> a and b -> S may intersect. Consider the graph below:
Here, if we used dist[a] + dist[b] + 1, then we'd report a cycle of length 2 + 3 + 1 = 6, when in reality no cycle exists at all because the path from S -> a is a prefix of the path from S -> b.
So, we need to ensure that for (a, b), the path S -> a isn't a prefix of S -> b (or vice versa). Observe that this simply equivalent to checking if parent_of[a] != b && parent_of[b] != a. So as long as that condition is true, then we can use dist[a] + dist[b] + 1.
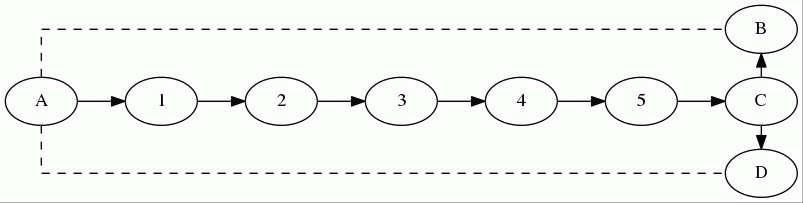
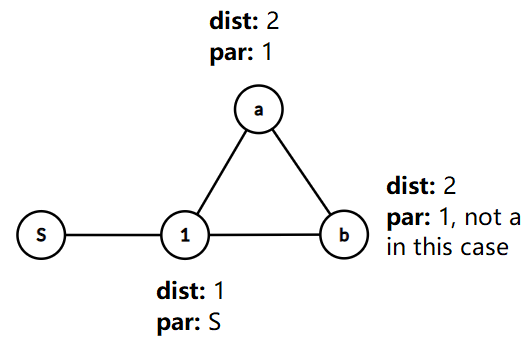
But, you might ask, what if the two paths S -> a and S -> b aren't prefixes of each other, but they still intersect, like below?
Here, because par[b] equals 1 and not a, neither of S->a and S->b are prefixes of the other, so we would report a cycle of length dist[a] + dist[b] + 1 = 2 + 2 + 1 = 5 (representing the cycle S -> 1 -> a -> b -> 1 -> S)! Clearly, this is not a simple cycle, and so shouldn't be counted. However, observe that we do not actually need to change the algorithm to correct this, because (a) we never reports a cycle when one doesn't exist (For instance, although S -> 1 -> a -> b -> 1 -> S isn't a simple cycle, it contains the simple cycle 1 -> a -> b -> 1. Essentially, whenever S->a and S->b share a prefix, then there is an existing cycle that can be found by removing their shared prefix), and (b) this only ever reports cycles longer than the minimum-length cycle, meaning we won't ever get a wrong answer (we won't ever get a cycle shorter than the shortest cycle). And lastly, we will always find the shortest cycle whenever we test a starting node that lies within that cycle, so we will always get the correct answer.
So, to recap:
dist[i] and par[i].(a, b), and find the shortest cycle starting from S that passes through that edge.parent_of[a] != b && parent_of[b] != a (meaning neither of the paths S->a and S->b are a prefix of the other, so we don't ever report a cycle where none exists), we have a cycle of length dist[a] + dist[b] + 1.dist[a] + dist[b] + 1 over all edges over all starting nodes, yields the answer.Time Complexity: O(V(V + E)), since for each of the V starting nodes we run a O(V + E) BFS.
Space Complexity: O(V + E), since we need O(V + E) for the adjacency list and O(V) for the arrays/queues used in the BFS.
Implementation in C++:
int shortest_cycle_length(const vector<vector<int>> &adj) {
int N = adj.size(), INF = N + 1;
int shortest_cycle = INF; // cycle length must be <= N
// Test every possible starting node of the shortest cycle
for (int starting_node = 0; starting_node < N; ++starting_node) {
// Find the shortest cycle that starts (and ends) at starting_node
// BFS, finding for each node its shortest distance from starting_node
// as well as its parent node in the shortest path to it
queue<int> Q;
vector<bool> visited(N, false);
vector<int> dist(N, INF), parent_of(N, -1);
Q.push(starting_node);
visited[starting_node] = true;
dist[starting_node] = 0;
while (!Q.empty()) {
int curr = Q.front();
Q.pop();
for (int next_node : adj[curr]) {
// If we haven't visited next_node, enqueue it (normal BFS)
if (!visited[next_node]) {
visited[next_node] = true;
dist[next_node] = dist[curr] + 1;
parent_of[next_node] = curr;
Q.push(next_node);
}
// Otherwise, we have visited next_node previously.
else if (parent_of[curr] != next_node) {
// ^^ Note that we don't need to check if parent_of[next_node] = curr,
// because that can never happen
// Then there is a cycle from starting_node through curr <=> next_node
// Specifically: starting_node -> curr -> next_node -> starting_node
// Clearly, the shortest length of this cycle is (dist[curr] + dist[next_node] + 1)
shortest_cycle = min(shortest_cycle, dist[curr] + dist[next_node] + 1);
}
}
}
}
// return -1 if no cycle exists, otherwise return shortest_cycle
return (shortest_cycle == INF ? -1 : shortest_cycle);
}
Note that in this implementation, I create new dist and par arrays for each starting node. If you just allocate them once at the beginning and reset them for each new starting node, you'll probably save a bit of time.
Also, notice that instead of iterating over all edges after the BFS is complete and finding the shortest cycle through each edge, I do it during the BFS. When we're at curr_node and wanting to move to next_node, then if next_node has already been visited (so we know it's dist and par values), I find right then and there the shortest cycle through the edge (curr_node, next_node). To do this, we just need to check if parent_of[curr_node] != next_node && parent_of[next_node] != curr_node, but then observe that parent_of[next_node] can never equal curr_node, because otherwise that means next_node could not have been visited previously. As a result, we only need to check if parent_of[curr_node] != next_node; if this condition is satisfied, the minimize the answer with dist[curr_node] + dist[next_node] + 1.
Here I shows one possible solution by combining DFS and BFS inspired by this baeldung blog.
I offer some notes for the pseudocode:
depth[node] to -1 by
First, we check if the depth of the current node is not equal to -1, which means this node has been visited before, and we have a cycle.
d-depth[node] is the length of the cycle because depth[node]!=-1 means it is one ancestor.
And MIN (answer, ShortestCycle(G, v, node, d + 1, depth) connects the back edge to the path of tree edges by d+1.visited array, so it is not one mere DFS.
And $for v \in G[node].neighbors do$ implies the BFS behavior.
Note that we used all the neighbors of the current node, except for the parent.
if v != parent is similar to the Labo's reference to avoid unnecessary backtracking.
This will cause our answer to always be equal 2 from the option of going back and forth any edge. Thus, we don’t return directly to the parent node but move to visit other nodes.
depth is one stack structure to store the path sequence related with the possible cycle sequence.ShortestCycle(G, 1, -1, i, {-1}) is also ok. Here we assume depth starting index is 1 instead of 0 normally and -1 is one invalid node index which we can use to indicate no parent for the root node.In summary, this algorithm enumerates for all spanning trees generated by DFS with one fixed root. The above BFS behavior implies it can find the shortest cycle.
The space complexity is right based on the stack structrue where G has one constant space, node, parent, d may be stored in the stack due to the recursive algorithm which has O(d) where d is the maximal depth V. depth also has O(d) due to its stack structure (i.e. will drop the added node when returning to the caller) and has the maximal depth V.
The time complexity shown in the blog IMHO is wrong.
The reason behind this complexity is that we’re visiting each vertex at most twice, and each edge at most once.
branching factor (See QA_1)
Here based on BFS, each node v can branch out at most deg(v) nodes (most of time this will less due to that we have depth to ensure no duplicate nodes in one specific branch when DFS. Notice it doesn't ensure no duplicate for the whole tree-like graph (See QA_1) which allows redundant paths)
depth
Then the depth of this tree-like graph is at most |V| when there is one Hamiltonian path.
Then we have O(max(deg(v))^{|V|+1}), i.e. O(n^{|V|+1}) where n is the number of vertices, nodes in this tree-like graph (See QA_1). Here since max(deg(v)) is not one constant, so I didn't drop the max(deg(v)) factor when calculating max(deg(v))+...+max(deg(v))^{|V|}.
time complexity of each node
For each node we execute ShortestCycle, here we don't use the adjacency list with time complexity O(deg(v)) to check adjacency but use depth[node] which has O(1) time complexity. And $for v \in G[node].neighbors do$ is already contained when branching out nodes and get the node number. So O(1) for each node.
In summary we have time complexity O(n^{|V|+1}).
Here I don't one very exact estimate for time complexity because we are only to get one upper bound for O(). Anyone with one better understanding of the algorithm in the blog can improve this answer.
Thanks in advance
© 2022 - 2024 — McMap. All rights reserved.