Quantum Computing and Encryption Breaking

Question

I read a while back that Quantum Computers can break most types of hashing and encryption in use today in a very short amount of time(I believe it was mere minutes). How is it possible? I've tried reading articles about it but I get lost at the a quantum bit can be 1, 0, or something else. Can someone explain how this relates to cracking such algorithms in plain English without all the fancy maths?

Sorry

Off topic? heh. Where do you suppose this belongs? Quantum Overflow? – Sorry

there you go! Now you've observed it - the site has disappeared. – Macmillan

@Martin Beckett: LOL. :-D Actually the first quantum joke I've ever read. – Soni

@Paja: thats really your first quantum joke? Try this: A police officer pulls over Heisenberg, and starts: "Do you know how fast you were going?". Heisenberg responds with "No, but I know exactly where I am!" – Stocking

Answer 1

Preamble: Quantum computers are strange beasts that we really haven't yet tamed to the point of usefulness. The theory that underpins them is abstract and mathematical, so any discussion of how they can be more efficient than classical computers will inevitably be long and involved. You'll need at least an undergraduate understanding of linear algebra and quantum mechanics to understand the details, but I'll try to convey my limited understanding!

---

The basic premise of quantum computation is quantum superposition. The idea is that a quantum system (such as a quantum bit, or qubit, the quantum analogue of a normal bit) can, as you say, exist not only in the 0 and 1 states (called the computational basis states of the system), but also in any combination of the two (so that each has an amplitude associated with it). When the system is observed by someone, the qubit's state collapses into one of its basis states (you may have heard of the Schrödinger's cat thought experiment, which is related to this).

Because of this, a register of n qubits has 2^n basis states of its own (these are the states that you could observe the register being in; imagine a classical n-bit integer). Since the register can exist in a superposition of all these states at once, it is possible to apply a computation to all 2^n register states rather than just one of them. This is called quantum parallelism.

Because of this property of quantum computers, it may seem like they're a silver bullet that can solve any problem exponentially faster than a classical computer. But it's not that simple: the problem is that once you observe the result of your computation, it collapses (as I mentioned above) into the result of just one of the computations – and you lose all of the others.

The field of quantum computation/algorithms is all about trying to work around this problem by manipulating quantum phenomena to extract information in fewer operations than would be possible on a classical computer. It turns out that it's very difficult to contrive a "quantum algorithm" that is faster than any possible classical counterpart.

The example you ask about is that of quantum cryptanalysis. It's thought that quantum computers might be able to "break" certain encryption algorithms: specifically, the RSA algorithm, which relies on the difficulty of finding the prime factors of very large integers. The algorithm which allows for this is called Shor's algorithm, which can factor integers with polynomial time complexity. By contrast the best classical algorithm for the problem has (almost) exponential time complexity, and the problem is hence considered "intractable".

If you want a deeper understanding of this, get a few books on linear algebra and quantum mechanics and get comfortable. If you want some clarification, I'll see what I can do!

---

Aside: to better understand the idea of quantum superposition, think in terms of probabilities. Imagine you flip a coin and catch it on your hand, covered so that you can't see it. As a very tenuous analogy, the coin can be thought of as being in a superposition of the heads and tails "states": each one has a probability of 0.5 (and, naturally, since there are two states, these probabilities add up to 1). When you take your hand away and observe the coin directly, it collapses into either the heads state or the tails state, and so the probability of this state becomes 1, while the other becomes 0. One way to think about it, I suppose, is a set of scales that is balanced until observation, at which point it tips to one side as our knowledge of the system increases and one state becomes the "real" state.

Of course, we don't think of the coin as a quantum system: for all practical purposes, the coin has a definite state, even if we can't see it. For genuine quantum systems, however (such as an individual particle trapped in a box), we can't think about it in this way. Under the conventional interpretation of quantum mechanics, the particle fundamentally has no definite position, but exists in all possible positions at once. Only upon observation is its position constrained in space (though only to a limited degree; cf. uncertainty principle), and even this is purely random and determined only by probability.

By the way, quantum systems are not restricted to having just two observable states (those that do are called two-level systems). Some have a large but finite number, some have a countably infinite number (such as a "particle in a box" or a harmonic oscillator), and some even have an uncountably infinite number (such as a free particle's position, which isn't constrained to individual points in space).

Caryl

+1 nice, though Schroedinger's cat is actually a thought experiment meant to show just how ridiculous the interpretation of Quantum Mechanics is which states that a particle has no state until it's observed ("Copenhagen intepretation")... – Falconiform

@BlueRaja: You're correct. It's still a consequence of superposition, though, which is all I was trying to say :) – Caryl

@Earlz: I think a PhD in theoretical physics is probably more useful :) – Caryl

"Under quantum mechanics, the electron has no definite position" - once again, that is just one interpretation of QM. There are others, even some in which all particles have definite positions (but are required to be superluminously connected to every other particle in the universe...) - and all the interpretations are consistent with QM. See here and, more generally, here. – Falconiform

@BlueRaja: Again, true, but the Copenhagen interpretation is the prevailing understanding of QM and is the simplest to explain! – Caryl

The particle can have a definite position (well, in space-time) but that means you'll know next to nothing about its momentum. Heisenberg showed that there was a minimum amount of uncertainty that you could have in total about the combination of position and momentum of any quantum system. (There are other pairs of properties that are equivalently linked.) AIUI, the problem relates to the fact that measuring position disturbs momentum, and measuring momentum disturbs position. Might be wrong on that last point though. – Sedentary

@Donal: What you're talking about is the HUP (which I alluded to in my answer), but this is not the same thing as quantum indeterminacy, which is what I was referring to. Prior to observation, the values of the system's observables are indeterminate (the system is in a superposition). Following observation, they are no longer indeterminate, but they are still to some extent uncertain, as you say. As for your last point, it's not so much a question of the experimental imperfections of measurement, but rather a fundamental statement about the limitations of knowledge under quantum mechanics. – Caryl

@Will: As I understand it, you can't really decouple measurement from knowledge except in a Platonic sense (which is just willful BS). Mind you, I philosophically tend towards accepting that Schrödinger's thought experiment is reasonable and that when you make an observation, from my perspective you've just become entangled with that bit of quantum state. (The net effect is the same.) Decoherence is just the spreading of a quantum state over far too many particles to ever hope to figure out what it was (especially given there's lots of other existing states there too). – Sedentary

@Donal: I agree about your interpretation of Schrödinger's cat; it seems to lend itself to a solipsist view of the world in which the self is the only observer and everyone else is just an "aspect" of the universe. Very interesting! – Caryl

@Will: Well, it's either that or worry about what constitutes an observer, which I find far more philosophically worrying. I'd much rather have myself be the only special observer, and then only from my perspective. From your perspective, I'm nothing special in the observation stakes (but you are). I don't know if this what the Many Worlds interpretation is; I think there's only one world, but it's QM all the way. – Sedentary

I've read that if quantum computing works out, that'd mean some fundamental theories of computing would be wrong. What's the deal on that? – Vulcan

@Jeff: Can you be more specific? – Caryl

In my texbook (Algorithms by Sanjoy Dasgupta et al.) there's a bit stating: "...a T-step computation on any computer takes at most some polynomially equivalent to T steps on another. This fundamental principle is called the extended Church-Turing thesis. Quantum computers violate this fundamental thesis and therefore call into question some of our most basic assumptions about computers". It later says: "...What if all these efforts implementing quantum computers fail?.... it would point to some fundamental flaw in quantum physics, a theory that has stood unchallenged for a century". – Vulcan

Answer 2

The Wikipedia article does a very good job of explaining this.

In short, if you have N bits, your quantum computer can be in 2^N states at the same time. Similar conceptually to having 2^N CPU's processing with traditional bits (though not exactly the same).

Calves

I agree with this summary, but be aware that this is a simplification. From this simple picture one easily gets the idea that quantum computers could solve most exponentially scaling computer problems like optimization problems. They cannot. For more details what can be solved using quantum computers and what cannot, see: medium.com/twodigits/… – Scammony

Answer 3

It's highly theoretical at this point. Quantum Bits might offer the capability to break encryption, but clearly it's not at that point yet.

At the Quantum Level, the laws that govern behavior are different than in the macro level.

To answer your question, you first need to understand how encryption works.

At a basic level, encryption is the result of multiplying two extremely large prime numbers together. This super large result is divisible by 1, itself, and these two prime numbers.

One way to break encryption is to brute force guess the two prime numbers, by doing prime number factorization.

This attack is slow, and is thwarted by picking larger and larger prime numbers. YOu hear of key sizes of 40bits,56bits,128bits and now 256,512bits and beyond. Those sizes correspond to the size of the number.

The brute force algorithm (in simplified terms) might look like

for(int i = 3; i < int64.max; i++)
{
  if( key / i is integral)
  {
    //we have a prime factor
  }
}

So you want to brute force try prime numbers; well that is going to take awhile with a single computer. So you might try grouping a bunch of computers together to divide and conquer. That works, but is still slow for very large keysizes.

How a quantum bit address this is that they are both 0 and 1 at the same time. So say you have 3 quantum bits (no small feat mind you).

With 3 qbits, your program can have the values of 0-7 simulatanously

(000,001,010,011 etc)

, which includes prime numbers 3,5,7 at the same time.

so using the simple algorithm above, instead of increasing i by 1 each time, you can just divide once, and check

0,1,2,3,4,5,6,7

all at the same time.

Of course quantum bits aren't to that point yet; there is still lots of work to be done in the field; but this should give you an idea that if we could program using quanta, how we might go about cracking encryption.

Estellaestelle

Many parts of this answer are misleading. Not all encryption depends on factoring the product of two primes. RSA depends on factorization, but other algorithms (such as AES) don't. RSA keys are not 40, 64 or 128 bits. These days, they start at 1024. You don't factor by brute force search. The best technique to date is the "General Number Field Sieve". It is much faster than brute force (so 1024-bit RSA gives the same security as 80-bit symmetric crypto). Quantum attacks on RSA use the fast Fourier transform, not brute force. In no sense do you check 0,1,2,3,4,5,6,7 at the same time. – Adscititious

The original question was"Can someone explain how this relates to cracking such algorithms in plain English without all the fancy maths? " So explain to someone who doesn't really understand "superposition" about GNFS and FFT's using simplified terms. Brute force is the easiest way to describe an attack; no where did I say it was the attack of choice. You are right, not all encryption types are based on prime number factorization; but in terms of this discussion (ie how can quantum computing crack encryption) those types of encryption are all that matter. – Estellaestelle

@WilliamWhyte: How can Fourier Transform be used to encryption purposes? Note: I understand the continuous Fourier Transform but not so well the DFT. – Krug

The Fourier Transform isn't used for encryption purposes in this setting; it's used to break RSA. There's a great explanation at scottaaronson.com/blog/?p=208. There may be examples of how it's used for encryption -- for example, in the signature algorithm PASS which I've contributed to, the public key can be thought of as part of the Fourier transform of the private key -- but my reference above was to its use in Shor's algorithm, which is a use for cryptanalysis rather than directly for encryption. – Adscititious

Answer 4

A quantum computer can implement Shor's algorithm which can quickly perform prime factorization. Encryption systems are build on the assumption that large primes can not be factored in a reasonable amount of time on a classical computer.

Vallievalliere

That's one example of an algorithm well-suited to quantum computing, though there are many others. – Calves

Some encryption systems are based on that assumption, typically used in public-key systems. – Dioptase

Answer 5

Almost all our public-key encryptions (ex. RSA) are based solely on math, relying on the difficulty of factorization or discrete-logarithms. Both of these will be efficiently broken using quantum computers (though even after a bachelors in CS and Math, and having taken several classes on quantum mechanics, I still don't understand the algorithm).

However, hashing algorithms (Ex. SHA2) and symmetric-key encryptions (ex. AES), which are based mostly on diffusion and confusion, are still secure.

Falconiform

If quantum computers are developed, the effective keylength of symmetric ciphers will be halved. So a 256-bit AES key will give the same security as a 128-bit AES key does today. It's still secure, but systems that only use 128-bit AES will have to be changed. – Adscititious

@William: Interesting, I did not know that. For those interested, information about the algorithm can be found here – Falconiform

Answer 6

In the most basic terms, a normal no quantum computer works by operating on bits (sates of on or off) uesing boolean logic. You do this very fast for lots and lots of bits and you can solve any problem in a class of problems that are computable.

However they are "speed limits" namely something called computational complexity.This in lay mans terms means that for a given algorithm you know that the time it takes to run an algorithm (and the memory space required to run the algorithm) has a minimum bound. For example a algorithm that is O(n^2) means that for a data size of n it will require n^2 time to run.

However this kind of goes out the window when we have qbits (quantum bits) when you are doing operations on qbits that can have "in between" values. algorithms that would have very high computational complexity (like factoring huge numbers, the key to cracking many encryption algorithms) can be done in much much lower computational complexity. This is the reason that quantum computing will be able to crack encrypted streams orders of magnitude quicker then normal computers.

Breather

Answer 7

First of all, quantum computing is still barely out of the theoretical stage. Lots of research is going on and a few experimental quantum cells and circuits, but a "quantum computer" does not yet exist.

Second, read the wikipedia article: http://en.wikipedia.org/wiki/Quantum_computer

In particular, "In general a quantum computer with n qubits can be in an arbitrary superposition of up to 2^n different states simultaneously (this compares to a normal computer that can only be in one of these 2^n states at any one time). "

What makes cryptography secure is the use of encryption keys that are very long numbers that would take a very, very long time to factor into their constituent primes, and the keys are sufficiently long enough that brute-force attempts to try every possible key value would also take too long to complete.

Since quantum computing can (theoretically) represent a lot of states in a small number of qubit cells, and operate on all of those states simultaneously, it seems there is the potential to use quantum computing to perform brute-force try-all-possible-key-values in a very short amount of time.

If such a thing is possible, it could be the end of cryptography as we know it.

Mas

Update: Quantum computers are now being made (though with very few Q bits and with near-zero degree cooling required) venturebeat.com/2011/05/27/first-quantum-computer-sold – Sorry

Answer 8

quantum computers etc all lies. I dont believe these science fiction magazines. in fact rsa system is based on two prime numbers and their multipilation. p1,p2 is huge primes p1xp2=N modulus. rsa system is like that choose a prime number..maybe small its E public key (p1-1)*(p2-1)=R find a D number that makes E*D=1 mod(R) we are sharing (E,N) data as public key publicly we are securely saving (D,N) as private.

To solve this Rsa system cracker need to find prime factors of N. *mass of the Universe is closer to 10^53 kg* electron mass is 9.10938291 × 10^-31 kilograms if we divide universe to electrons we can create 10^84 electrons. electrons has slower speeds than light. its move frequency can be 10^26 if anybody produces electron size parallel rsa prime factor finders from all universe mass. all universe can handle (10^84)*(10^26)= 10^110 numbers/per second.

rsa has limitles bits of alternative prime numbers. maybe 4096 bits 4096 bit rsa has 10^600 possible prime numbers to brute force. so your universe mass quantum solver need to make tests during 10^500 years.

rsa vs universe mass quantum computer 1 - 0

maybe quantum computer can break 64/128 bits passwords. because 128 bit password has 10^39 possible brute force nodes.

Fishery

I do agree that factorization by brute-force trying out all possible factors would take too long. But that does not mean that more clever algorithms are not possible (this is even true without thinking about quantum computers). As an example consider the problem of finding out if a given number N is or is not a prime number. If N is, say, a 1000 digit number one could also think that this is an impossible task, but in fact this can be done on ordinary computers, see en.wikipedia.org/wiki/Primality_test The test is just more complicated than trying out every possible divisor. – Scammony

Answer 9

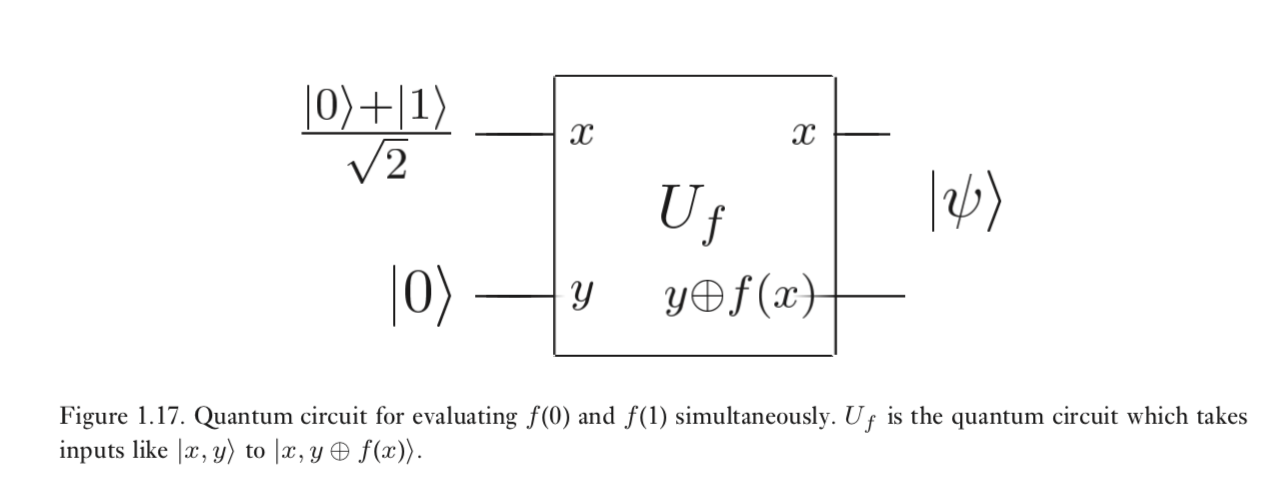
This circuit is a good start to understand how qubit parallelism works. The 2-qubits-input is on the left side. Top qubit is x and bottom qubit ist y. The y qubit is 0 at the input, just like a normal bit. The x qubit on the other hand is in superposition at the input. y (+) f(x) stands here for addition modulo 2, just meaning 1+1=0, 0+1=1+0=1. But the interesting part is, since the x-qubit is in superposition, f(x) is f(0) and f(1) at the same time and we can perform the evaluation of the f function for all states simultaneously without using any (time consuming) loops. Having enough quibits we can branch this into endlessly complicating curcuits.

Pair

Answer 10

Even more bizarr imo. is the Grover's algorithm. As input we get here an unsorted array of integers with arraylength = n. What is the expected runtime of an algorithm, that finds the min value of this array? Well classically we have at least to check every 1..n element of the array resulting in an expected runtime of n. Not so for quantum computers, on a quantum computer we can solve this in expected runtime of maximum root(n), this means we don't even have to check every element to find the guaranteed solution...

Pair