OpenCV triangulatePoints handedness

Question

I have two cameras attached rigidly side by side looking in parallel directions.

Projection matrix for left camera

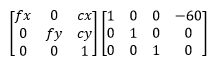
Projection matrix for right camera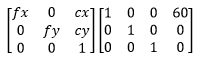

When I perform triangulatePoints on the two vectors of corresponding points, I get the collection of points in 3D space. All of the points in 3D space have a negative Z coordinate.

So, to get to the bottom of this...

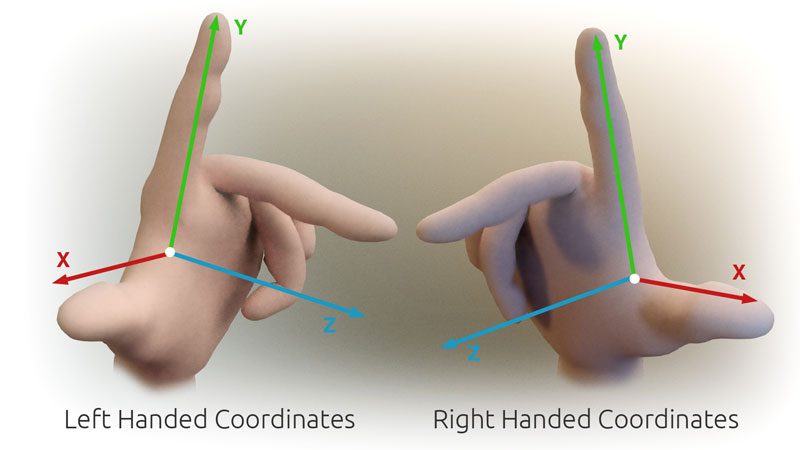
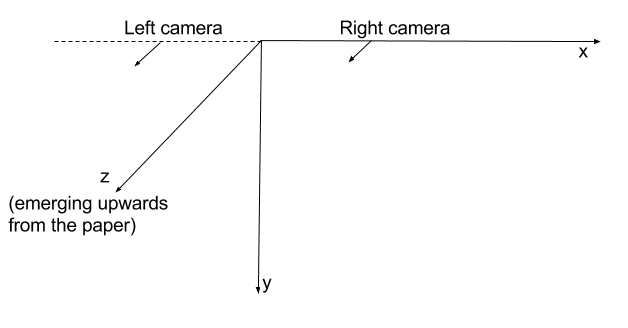
My assumption was that OpenCV uses Right Hand coordinate system.

The handedness reminder:

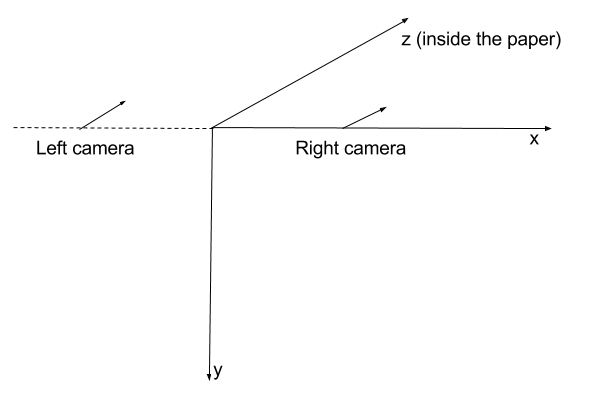
I assume that the initial orientation of each camera is directed in the positive Z axis direction.

So, by using the projection matrices like the ones I presented in the beginning, I would assume that the cameras are positioned in space like this:

This assumption is in conflict with what I observe when I get negative Z corrdinates for the traingulated points. The only explanation I can think of is that OpenCV in fact uses the Left Hand coordinate system. So, with the projection matrices I stated in the beginning, this is how the cameras are positioned in space:

This would indicate that my left camera in this situation is not on the left side. And this is why I am getting negative depth for points.

Moreover, if I try to combine triangulatePoints with solvePnP I run into problems.

I use the output of triangulatePoints as an input to solvePnP. I expect to get the camera coordinates near the origin of 3D coordinate system. I expect for calculated camera position to match the projection matrices used in the beginning. But this is not happening. I get some completely wild results, missing the expected values by over 10 times the baseline length.

Example

This example is more complete representation of the problem than what is stated above.

points3D

Here is the code for generating these points.

Movin on, setting up camera A and camera D...

Mat cameraMatrix = (Mat_<double>(3, 3) <<
    716.731, 0, 660.749,
    0, 716.731, 360.754,
    0, 0, 1);
Mat distCoeffs = (Mat_<double>(5, 1) << 0, 0, 0, 0, 0);



Mat rotation_a = Mat::eye(3, 3, CV_64F); // no rotation
Mat translation_a = (Mat_<double>(3, 1) << 0, 0, 0); // no translation
Mat rt_a;
hconcat(rotation_a, translation_a, rt_a);
Mat projectionMatrix_a = cameraMatrix * rt_a; 

Mat rotation_d = (Mat_<double>(3, 1) << 0, CV_PI / 6.0, 0); // 30° rotation about Y axis
Rodrigues(rotation_d, rotation_d); // convert to 3x3 matrix
Mat translation_d = (Mat_<double>(3, 1) << 100, 0, 0);
Mat rt_d;
hconcat(rotation_d, translation_d, rt_d);
Mat projectionMatrix_d = cameraMatrix * rt_d;

What are the pixel coordinates of points3D when observed by projections A and D.

Mat points2D_a = projectionMatrix_a * points3D;
Mat points2D_d = projectionMatrix_d * points3D;

I put them in vectors:

vector<Point2f> points2Dvector_a, points2Dvector_d;

After that, I generate the 3D points again.

Mat points3DHomogeneous;
triangulatePoints(projectionMatrix_a, projectionMatrix_d, points2Dvector_a, points2Dvector_d, points3DHomogeneous);
Mat triangulatedPoints3D;
transpose(points3DHomogeneous, triangulatedPoints3D);
convertPointsFromHomogeneous(triangulatedPoints3D, triangulatedPoints3D);

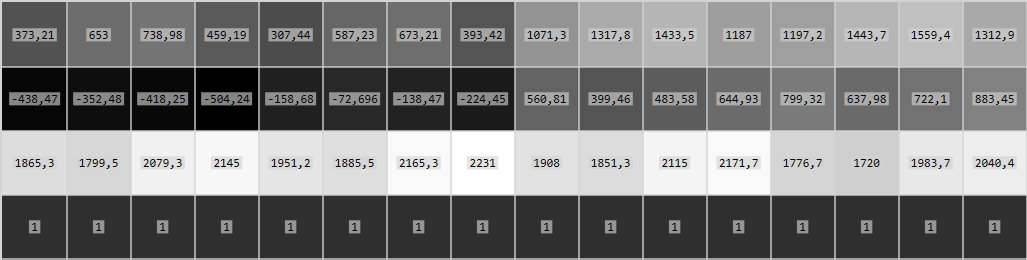
Now, triangulatedPoints3D start out like this:

and they are identical to points3D.

And then the last step.

Mat rvec, tvec;
solvePnP(triangulatedPoints3D, points2Dvector_d, cameraMatrix, distCoeffs, rvec, tvec);

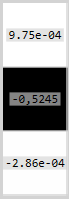
Resulting rvec and tvec:

I had hoped to get something more similar to the transformations used in creation of projectionMatrix_d, i.e. translation of (100, 0, 0) and rotation of 30° about Y axis.

If I use inverted transformations when creating projection matrix, like this:

Mat rotation_d = (Mat_<double>(3, 1) << 0, CV_PI / 6.0, 0); // 30° rotation about Y axis
Rodrigues(-rotation_d, rotation_d); // NEGATIVE ROTATION
Mat translation_d = (Mat_<double>(3, 1) << 100, 0, 0);
Mat rt_d;
hconcat(rotation_d, -translation_d, rt_d); // NEGATIVE TRANSLATION
Mat projectionMatrix_d = cameraMatrix * rt_d;

then I get rvec and tvec:

And that makes much more sense. But then I change the starting transformation so that the rotation is negative CV_PI / 6.0 -> -CV_PI / 6.0 and the resulting rvec and tvec are:

I would like to find an explanation to why this is happening. Why am I getting such weird results from solvePnP.

Kinson

I can confirm that OpenCV uses the right-handed coordinate system and I also use triangulatePoints and solvePnP regularly. I am not exactly sure what your question is, but based on the description of your problem, I would start by investigating your input data. More details would be needed to find out exactly what is going on (e.g. camera matrices, actual code, input data samples, etc). – Hawn

Thank you for your response. I expanded the question. – Kinson

I can confirm that the rotation and translation values used in generation of projection matrices are not supposed to reflect the movement of the camera but rather the movement of the points. So, if camera moved 100 units to the left, that's the same as if the points moved 100 units to the right. But the movement to the right should be used in calculation of projection matrix. – Kinson

I have the same problem... anyone can help?? – Dryad

Answer 1

OpenCV coordinate system is right-handed, the answer here gives an illustrative example about OpenCV camera system. I guess the confusion is about rvec and tvec, the latter does not give the translation of the camera but it points to the world origin. The first answer here explains it based on an example. You can get the actual projection matrix from the output of solvePnP by a simple matrix multiplication, the details are here in the first answer.

Intercede