I'm taking the following approach to animate a star field across the screen, but I'm stuck for the next part.
JS
var c = document.getElementById('stars'),
ctx = c.getContext("2d"),
t = 0; // time
c.width = 300;
c.height = 300;
var w = c.width,
h = c.height,
z = c.height,
v = Math.PI; // angle of vision
(function animate() {
Math.seedrandom('bg');
ctx.globalAlpha = 1;
for (var i = 0; i <= 100; i++) {
var x = Math.floor(Math.random() * w), // pos x
y = Math.floor(Math.random() * h), // pos y
r = Math.random()*2 + 1, // radius
a = Math.random()*0.5 + 0.5, // alpha
// linear
d = (r*a), // depth
p = t*d; // pixels per t
x = x - p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
(function draw(x,y) {
var gradient = ctx.createRadialGradient(x, y, 0, x + r, y + r, r * 2);
gradient.addColorStop(0, 'rgba(255, 255, 255, ' + a + ')');
gradient.addColorStop(1, 'rgba(0, 0, 0, 0)');
ctx.beginPath();
ctx.arc(x, y, r, 0, 2*Math.PI);
ctx.fillStyle = gradient;
ctx.fill();
return draw;
})(x, y);
}
ctx.restore();
t += 1;
requestAnimationFrame(function() {
ctx.clearRect(0, 0, c.width, c.height);
animate();
});
})();
HTML
<canvas id="stars"></canvas>
CSS
canvas {
background: black;
}
What it does right now is animate each star with a delta X that considers the opacity and size of the star, so the smallest ones appear to move slower.
Use p = t; to have all the stars moving at the same speed.
QUESTION
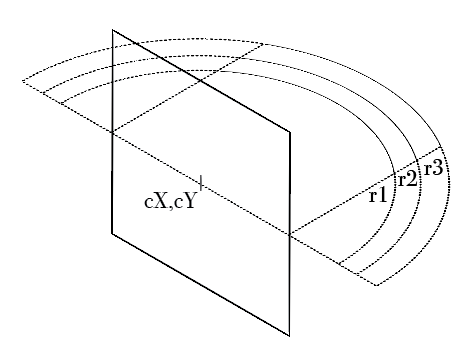
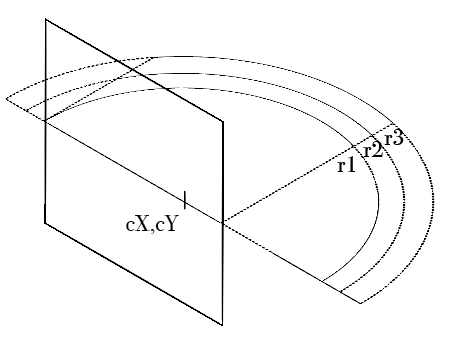
I'm looking for a clearly defined model where the velocities give the illusion of the stars rotating around the expectator, defined in terms of the center of the rotation cX, cY, and the angle of vision v which is what fraction of 2π can be seen (if the center of the circle is not the center of the screen, the radius should be at least the largest portion). I'm struggling to find a way that applies this cosine to the speed of star movements, even for a centered circle with a rotation of π.
These diagrams might further explain what I'm after:
Centered circle:
Non-centered:
Different angle of vision:
I'm really lost as to how to move forwards. I already stretched myself a bit to get here. Can you please help me with some first steps?
Thanks
UPDATE
I have made some progress with this code:
// linear
d = (r*a)*z, // depth
v = (2*Math.PI)/w,
p = Math.floor( d * Math.cos( t * v ) ); // pixels per t
x = x + p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
Where p is the x coordinate of a particle in uniform circular motion and v is the angular velocity, but this generates a pendulum effect. I am not sure how to change these equations to create the illusion that the observer is turning instead.
UPDATE 2:
Almost there. One user at the ##Math freenode channel was kind enough to suggest the following calculation:
// linear
d = (r*a), // depth
p = t*d; // pixels per t
x = x - p; // movement
x = x - w * Math.floor(x / w); // go around when x < 0
x = (x / w) - 0.5;
y = (y / h) - 0.5;
y /= Math.cos(x);
x = (x + 0.5) * w;
y = (y + 0.5) * h;
This achieves the effect visually, but does not follow a clearly defined model in terms of the variables (it just "hacks" the effect) so I cannot see a straightforward way to do different implementations (change the center, angle of vision). The real model might be very similar to this one.
UPDATE 3
Following from Iftah's response, I was able to use Sylvester to apply a rotation matrix to the stars, which need to be saved in an array first. Also each star's z coordinate is now determined and the radius r and opacity a are derived from it instead. The code is substantially different and lenghthier so I am not posting it, but it might be a step in the right direction. I cannot get this to rotate continuously yet. Using matrix operations on each frame seems costly in terms of performance.

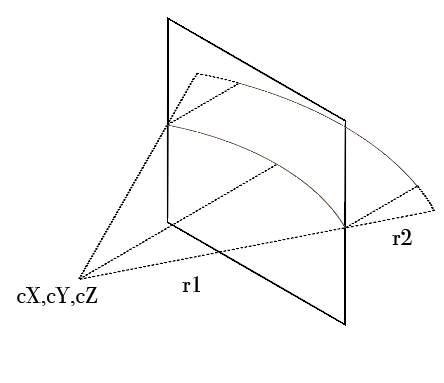
p = f(d)that uses a cosine to mimic the change of x in a circle of sectionv. As you point out, though, there'z a cZ variable that I did not put for the first example, I'll add it. – Sabulous