Efficient extraction of all sub-polygons generated by self-intersecting features in a MultiPolygon

Question

Starting from a shapefile containing a fairly large number (about 20000) of potentially partially-overlapping polygons, I'd need to extract all the sub-polygons originated by intersecting their different "boundaries".

In practice, starting from some mock-up data:

library(tibble)
library(dplyr)
library(sf)

ncircles <- 9
rmax     <- 120
x_limits <- c(-70,70)
y_limits <- c(-30,30)
set.seed(100) 
xy <- data.frame(
  id = paste0("id_", 1:ncircles), 
  x = runif(ncircles, min(x_limits), max(x_limits)),
  y = runif(ncircles, min(y_limits), max(y_limits))) %>% 
  as_tibble()

polys <- st_as_sf(xy, coords = c(2,3)) %>% 
  st_buffer(runif(ncircles, min = 1, max = 20)) 

plot(polys[1])  

I'd need to derive an sf or sp multipolygon containing ALL and ONLY the polygons generated by the intersections, something like:

(note that the colors are there just to exemplify the expected result, in which each "differently colored" area is a separate polygon which doesn't overlay any other polygon)

I know I could work my way out by analyzing one polygon at a time, identifying and saving all its intersections and then "erase" those areas form the full multipolygon and proceed in a cycle, but that is quite slow.

I feel there should be a more efficient solution for this, but I am not able to figure it out, so any help would be appreciated! (Both sf and sp based solutions are welcome)

UPDATE:

In the end, I found out that even going "one polygon at a time" the task is far from simple! I'm really struggling on this apparently "easy" problem! Any hints? Even a slow solution or hints for starting on a proper path would be appreciated!

UPDATE 2:

Maybe this will clarify things: the desired functionality would be similar to the one described here:

https://it.mathworks.com/matlabcentral/fileexchange/18173-polygon-intersection?requestedDomain=www.mathworks.com

UPDATE 3:

I awarded the bounty to @shuiping-chen (thanks !), whose answer correctly solved the problem on the example dataset provided. The "method" has however to be generalized to situations were "quadruple" or "n-uple" intersections are possible. I'll try to work on that in the coming days and post a more general solution if I manage !

Barroom

Are you interested in all the sub polygons or just the one that result from the intersection? (In the example, bottom center 'group', do you want green, blue and olive, or just the blue?) – Lipinski

I'm interested in all the subpolygons. However, the "areas" that don't intersect with anything are simple to extract using a sym_difference operator between each polygon and their union. What I0m struggling with are the intersections, and in particular the multiple intersections. – Barroom

@LoBu , look into this , i'm also trying around it – Federalist

Answer 1

This has now been implemented in R package sf as the default result when st_intersection is called with a single argument (sf or sfc), see https://r-spatial.github.io/sf/reference/geos_binary_ops.html for the examples. (I'm not sure the origins field contains useful indexes; ideally they should point to indexes in x only, right now they kind of self-refer).

Wean

That's great.I just tried it on a 1000-polygons test dataset and it perfectly addresses the problem! Thanks! – Barroom

@Edzer Pebesma, I got the evaluation error because of Self-intersection. Is there a simple way to solve this in the sf package? – Trophy

found the answer here: github.com/r-spatial/sf/issues/347: using st_make_valid or st_buffer(x, 0) – Trophy

Answer 2

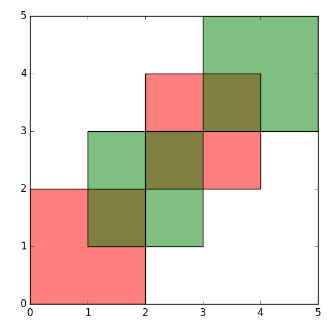
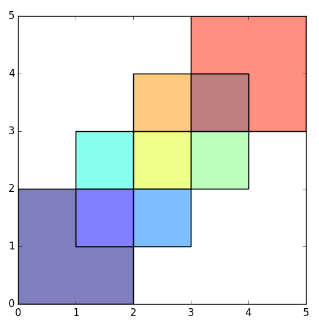
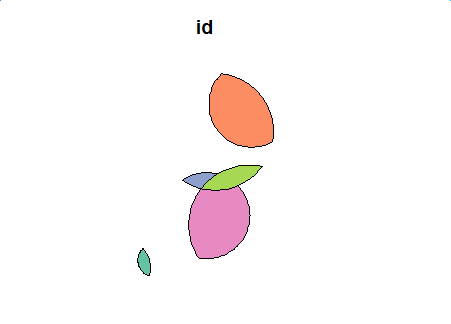Input

I modify the mock-up data a bit in order to illustrate the ability to deal with multiple attributes.

library(tibble)
library(dplyr)
library(sf)

ncircles <- 9
rmax     <- 120
x_limits <- c(-70,70)
y_limits <- c(-30,30)
set.seed(100) 
xy <- data.frame(
  id = paste0("id_", 1:ncircles), 
  val = paste0("val_", 1:ncircles),
  x = runif(ncircles, min(x_limits), max(x_limits)),
  y = runif(ncircles, min(y_limits), max(y_limits)),
  stringsAsFactors = FALSE) %>% 
  as_tibble()

polys <- st_as_sf(xy, coords = c(3,4)) %>% 
  st_buffer(runif(ncircles, min = 1, max = 20)) 
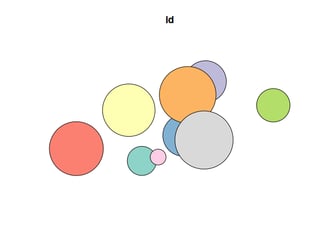
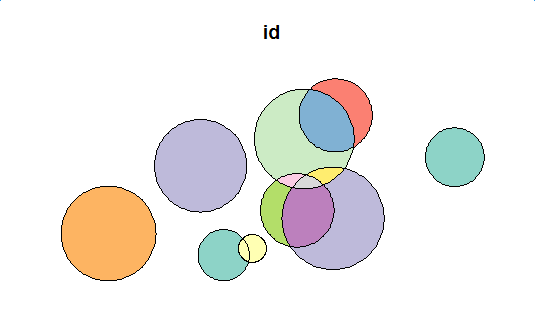
plot(polys[1])

Basic Operation

Then define the following two functions.

• cur: the current index of the base polygon
• x: the index of polygons, which intersects with cur
• input_polys: the simple feature of the polygons
• keep_columns: the vector of names of attributes needed to keep after the geometric calculation

get_difference_region() get the difference between the base polygon and other intersected polygons; get_intersection_region() get the intersections among the intersected polygons.

library(stringr)
get_difference_region <- function(cur, x, input_polys, keep_columns=c("id")){
  x <- x[!x==cur] # remove self 
  len <- length(x)
  input_poly_sfc <- st_geometry(input_polys)
  input_poly_attr <- as.data.frame(as.data.frame(input_polys)[, keep_columns])

  # base poly
  res_poly <- input_poly_sfc[[cur]]
  res_attr <- input_poly_attr[cur, ]

  # substract the intersection parts from base poly
  if(len > 0){
    for(i in 1:len){
      res_poly <- st_difference(res_poly, input_poly_sfc[[x[i]]])
    }
  }
  return(cbind(res_attr, data.frame(geom=st_as_text(res_poly))))
}


get_intersection_region <- function(cur, x, input_polys, keep_columns=c("id"), sep="&"){
  x <- x[!x<=cur] # remove self and remove duplicated obj 
  len <- length(x)
  input_poly_sfc <- st_geometry(input_polys)
  input_poly_attr <- as.data.frame(as.data.frame(input_polys)[, keep_columns])

  res_df <- data.frame()
  if(len > 0){
    for(i in 1:len){
      res_poly <- st_intersection(input_poly_sfc[[cur]], input_poly_sfc[[x[i]]])
      res_attr <- list()
      for(j in 1:length(keep_columns)){
        pred_attr <- str_split(input_poly_attr[cur, j], sep, simplify = TRUE)
        next_attr <- str_split(input_poly_attr[x[i], j], sep, simplify = TRUE)
        res_attr[[j]] <- paste(sort(unique(c(pred_attr, next_attr))), collapse=sep)
      }
      res_attr <- as.data.frame(res_attr)
      colnames(res_attr) <- keep_columns
      res_df <- rbind(res_df, cbind(res_attr, data.frame(geom=st_as_text(res_poly))))
    }
  }
  return(res_df)
}

First Level

Difference

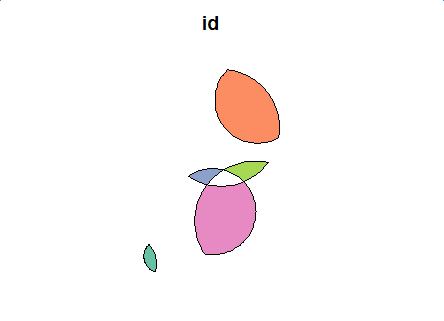
Let's see the difference function effect on the mock-up data.

flag <- st_intersects(polys, polys)

first_diff <- data.frame()
for(i in 1:length(flag)) {
  cur_df <- get_difference_region(i, flag[[i]], polys, keep_column = c("id", "val"))
  first_diff <- rbind(first_diff, cur_df)
}
first_diff_sf <- st_as_sf(first_diff, wkt="geom")
first_diff_sf
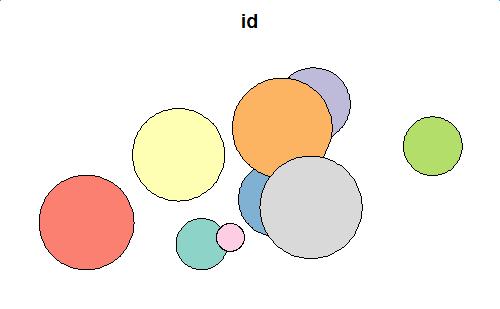
plot(first_diff_sf[1])

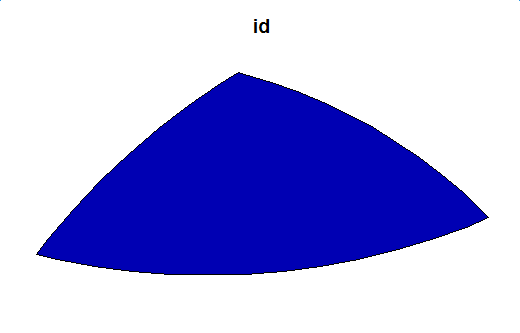
Intersection

first_inter <- data.frame()
for(i in 1:length(flag)) {
  cur_df <- get_intersection_region(i, flag[[i]], polys, keep_column=c("id", "val"))
  first_inter <- rbind(first_inter, cur_df)
}
first_inter <- first_inter[row.names(first_inter %>% select(-geom) %>% distinct()),]
first_inter_sf <- st_as_sf(first_inter, wkt="geom")
first_inter_sf
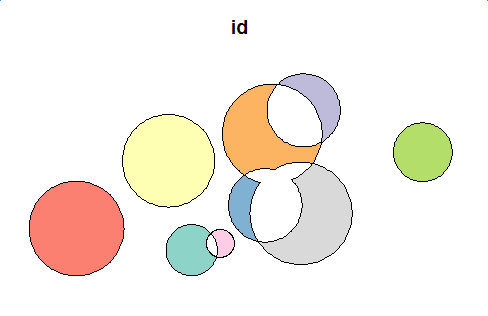
plot(first_inter_sf[1])

Second Level

use the intersection of first level as input, and repeat the same process.

Difference

flag <- st_intersects(first_inter_sf, first_inter_sf)
# Second level difference region
second_diff <- data.frame()
for(i in 1:length(flag)) {
  cur_df <- get_difference_region(i, flag[[i]], first_inter_sf, keep_column = c("id", "val"))
  second_diff <- rbind(second_diff, cur_df)
}
second_diff_sf <- st_as_sf(second_diff, wkt="geom")
second_diff_sf
plot(second_diff_sf[1])

Intersection

second_inter <- data.frame()
for(i in 1:length(flag)) {
  cur_df <- get_intersection_region(i, flag[[i]], first_inter_sf, keep_column=c("id", "val"))
  second_inter <- rbind(second_inter, cur_df)
}
second_inter <- second_inter[row.names(second_inter %>% select(-geom) %>% distinct()),]  # remove duplicated shape
second_inter_sf <- st_as_sf(second_inter, wkt="geom")
second_inter_sf
plot(second_inter_sf[1])

Get the distinct intersections of the second level, and use them as the input of the third level. We could get that the intersection results of the third level is NULL, then the process should end.

Summary

We put all the difference results into close list, and put all the intersection results into open list. Then we have:

• When open list is empty, we stop the process
• The results is close list

Therefore, we get the final code here (the basic two functions should be declared):

# init
close_df <- data.frame()
open_sf <- polys

# main loop
while(!is.null(open_sf)) {
  flag <- st_intersects(open_sf, open_sf)
  for(i in 1:length(flag)) {
    cur_df <- get_difference_region(i, flag[[i]], open_sf, keep_column = c("id", "val"))
    close_df <- rbind(close_df, cur_df)
  }
  cur_open <- data.frame()
  for(i in 1:length(flag)) {
    cur_df <- get_intersection_region(i, flag[[i]], open_sf, keep_column = c("id", "val"))
    cur_open <- rbind(cur_open, cur_df)
  }
  if(nrow(cur_open) != 0) {
    cur_open <- cur_open[row.names(cur_open %>% select(-geom) %>% distinct()),]
    open_sf <- st_as_sf(cur_open, wkt="geom")
  }
  else{
    open_sf <- NULL
  }
}

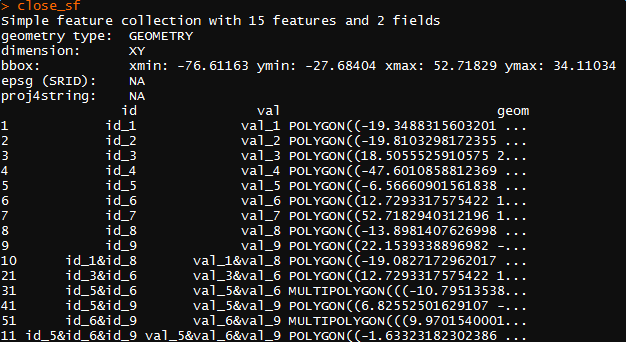
close_sf <- st_as_sf(close_df, wkt="geom")
close_sf
plot(close_sf[1])

Yerga

Very interesting, thanks ! I'll test it ASAP. By the way, before I work on it: would this deal well also in the case that we have "quadruple", or even "quintuple" intersections, or is it "limited" to max three overlapping polygons ? – Barroom

I suppose that it will work for general case, since the repeated process has no relationship with "max three overlapping". But remember to use the distinct intersections as the input for the next level. It took me some time to figure that out. – Yerga

Ok, thanks ! I'll give it a test run in different conditions and get back to you ! – Barroom

Hi. I was able to have a look at this only today. Works really well for the case at hand, thanks ! Howewer, this will need to be generalized for cases with more than "triple" intersections. Will look into it in the next days ! – Barroom

Answer 3

Not sure if it helps you since it is not in R but I think there is a good way to solve this problem using Python. There is a library called GeoPandas (http://geopandas.org/index.html) which has allows you to easily do geo operations. In steps what you would need to do is the following:

1. Load all Polygons into geopandas GeoDataFrames
2. Loop all GeoDataFrames running a union overlay operation (http://geopandas.org/set_operations.html)

The exact example is shown in the documentation.

Before operation - 2 Polygons

After operation - 9 Polygons

If there is anything unclear feel free to let me know! Hope it helps!

Anglophobia

Hi, thanks for the answer. If I interpret right the documentation, this would compute the set_operations between two different "multipolygons", which can be done also in "R" using sf or rgeos. My problem here is instead that I have a huge number of "single polygons" that can intersect, and the intersection areas can randomly "overlap". This generates additional "subpolygons" which are the ones I would like to "extract". See for example what happens for the three "big" circles in the middle of the example image. – Barroom

@LoBu you are right! It is not as simple as I thought. Another approach you could have is assigning a number 1 value to each polygon and then doo an aggregation on all of then. With this you would generate a third dimension in each sub-polygon. Having this done you just need to filter out all sub-polygons that still remain with assigned value equals to 1. Each overlaping sub-polygon will have number 2 or higher. I haven't had time to play a lot with geo queries to make sure this approach woul work or if it would be fast enough to run you dataset. What do you think? – Anglophobia

Hi. Sorry, what do you mean by an "aggregation" ? – Barroom

I mean adding up the the number 1 assigned to each polygon. So taking you figure as the example. The overlap between three big circles in the middle would have a value equals to 3; the overlap between 2 circles would have value equals to two and so on. Actually this would be a count on each overlapping area. – Anglophobia

That could work. Then I'd just need to re-polygonize according to "value". However, how could I do that ? I mean, how could I assign a value to the the different intersections (sorry, if I'm dumb... ) ? – Barroom

That is ok! You probably should look on how to do spatial operation with your polygons. There is a quite similar case discussed in this link gis.stackexchange.com/questions/190648/… – Anglophobia

That's promising. The problem is now to find a way to do this through scripting in "R". Any hints ? – Barroom

Let us continue this discussion in chat. – Anglophobia