I have to create a method that takes two integers, let them be n and m, and returns how many ways there are to sum m positive numbers to get n.
For example, a method call like this partition(6, 2) should return 3 because there are 3 ways possible. They are 5 + 1, 4 + 2, and 3 + 3. By the way, 4 + 2 is the same as 2 + 4, so the method should not count them as two distinct variations.
Does anybody know a solution to the problem?
Updated: n and m are not greater than 150.
To count all partitions of an integer n with m parts, a recursive algorithm is the obvious choice. For the case n, m, the algorithm runs through every option k = 1, 2, 3... for the first part, and for each of these options it recurses with the case n - k, m - 1. For example:
n = 16, m = 4
first part = 1 => recurse with n = 15, m = 3
first part = 2 => recurse with n = 14, m = 3
first part = 3 => recurse with n = 13, m = 3
etc...
After a number of recursions, the point is reached where m = 2; then the solutions are:
first part = 1 => second part = n - 1
first part = 2 => second part = n - 2
first part = 3 => second part = n - 3
etc...
So the number of solutions for m = 2 equals the number of options for the first part.
To count only unique solutions and discard duplicates, so that 2+4 and 4+2 are not both counted, only consider solutions where the parts form a non-decreasing sequence; for example:
n = 9, m = 3
partitions: 1+1+7 1+2+6 1+3+5 1+4+4
2+2+5 2+3+4
3+3+3
In a rising sequence, the value of the first part can never be greater than n / m.
To maintain a rising sequence, every recursion must use the value of the previous part as the minimum value for its parts; for example:
n = 9, m = 3
k = 1 => recurse with n = 8, m = 2, k >= 1 => 1+7 2+6 3+5 4+4
k = 2 => recurse with n = 7, m = 2, k >= 2 => 2+5 3+4
k = 3 => recurse with n = 6, m = 2, k >= 3 => 3+3
To avoid having to pass the minimum value with every recursion, every recursion n - k, m - 1, k is replaced with n - k - (m - 1) * (k - 1), m - 1, 1, which has the same number of solutions. For example:
n = 9, m = 3
k = 1 => recurse with n = 8, m = 2, k >= 1 => 1+7 2+6 3+5 4+4
k = 2 => recurse with n = 5, m = 2, k >= 1 => 1+4 2+3
k = 3 => recurse with n = 2, m = 2, k >= 1 => 1+1
Not only does this simplify the code, it also helps improve efficiency when using memoization, because sequences like 2+2+3, 3+3+4 and 5+5+6 are all replaced by their canonical form 1+1+2, and a smaller set of intermediate calculations are repeated more often.
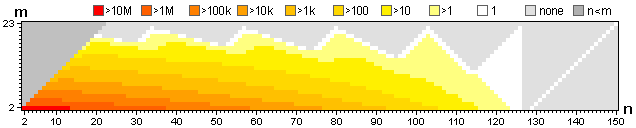
When partitioning with a recursive algorithm, many calculations are repeated numerous times. And with increasing values for n and m, the number of recursions quickly becomes huge; e.g. to solve case 150, 23 (illustrated below), case 4, 2 is calculated 23,703,672 times.
However, the number of unique calculations can never be greater than n * m. So by caching the result of each calculation in an n*m-sized array, no more than n * m calculation ever need be done; after having calculated a case once, the algorithm can use the stored value. This hugely improves the algorithm's efficiency; e.g. without memoization, 422,910,232 recursions are needed to solve the case 150, 23; with memoization, only 15,163 recursions are needed.
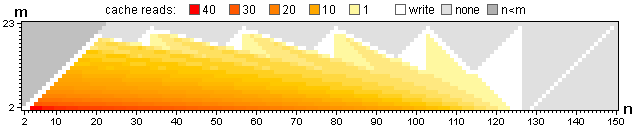
The illustration below shows cache reads and writes for this case. The grey cells are unused, the white cells are written but never read. There are a total of 2042 writes and 12697 reads.
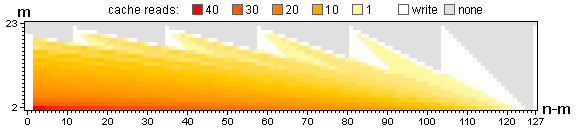
You'll notice that the triangles at the top left and bottom right are never used; and the closer the value of m is to n, the bigger the unused zones become. To avoid this waste of space, the parallellogram inbetween those two triangles can be skewed by 45°, by storing the value for n, m in n - m, m. The cache size is thus reduced from (n - 1) * (m - 1) to (n - m) * (m - 1), and the worst case for n,m <= 150 is no longer 149 * 149 = 22201, but 75 * 74 = 5550, less than 25% the size.
function partition(n, m) {
if (m < 2) return m;
if (n < m) return 0;
if (n <= m + 1) return 1;
var max = Math.floor(n / m);
if (m == 2) return max;
var count = 0;
for (; max--; n -= m) count += partition(n - 1, m - 1);
return count;
}
document.write(partition(6, 1) + "<br>"); // 1
document.write(partition(6, 2) + "<br>"); // 3
document.write(partition(9, 3) + "<br>"); // 7
document.write(partition(16, 4) + "<br>"); // 34
document.write(partition(150, 75) + "<br>"); // 8,118,264
// document.write(partition(150, 23)); // 1,901,740,434 (maximum for 150, takes > 10s)This version, which caches intermediate results, is much faster than the basic algorithm. Even this Javascript implementation solves the worst-case scenario for n=150 in less than a millisecond.
function partition(n, m) {
if (m < 2) return m;
if (n < m) return 0;
var memo = [];
for (var i = 0; i < n - 1; i++) memo[i] = [];
return p(n, m);
function p(n, m) {
if (n <= m + 1) return 1;
if (memo[n - 2][m - 2]) return memo[n - 2][m - 2];
var max = Math.floor(n / m);
if (m == 2) return max;
var count = 0;
for (; max--; n -= m) count += (memo[n - 3][m - 3] = p(n - 1, m - 1));
return count;
}
}
document.write(partition(150, 23) + "<br>"); // 1,901,740,434
// document.write(partition(1000, 81)); // 4.01779428811641e+29(The worst case for n = 1000, which is m = 81, solves to 4.01779428811641e+29, and this result is also returned nearly instantly. Because it exceeds Javascript's maximum safe integer of 253-1, this is of course not an exact result.)
This version uses the skewed cache indexes to reduces memory requirements.
function partition(n, m) {
if (m < 2) return m;
if (n < m) return 0;
var memo = [];
for (var i = 0; i <= n - m; i++) memo[i] = [];
return p(n, m);
function p(n, m) {
if (n <= m + 1) return 1;
if (memo[n - m][m - 2]) return memo[n - m][m - 2];
var max = Math.floor(n / m);
if (m == 2) return max;
var count = 0;
for (; max--; n -= m) count += (memo[n - m][m - 3] = p(n - 1, m - 1));
return count;
}
}
document.write(partition(150, 23) + "<br>"); // 1,901,740,434
document.write(partition(150, 75) + "<br>"); // 8,118,264
document.write(partition(150, 127) + "<br>"); // 1255You could use dynamic programming. Let f[n][m][k] be the number of of partitions of m non-decreasing positive numbers such that the sum is n and the last one is k. Then you could easily see that the update step would be:
f[n][m][k] → f[n+l][m+1][l] for every l≥ k
To get f[n][m], meaning the number of all partitions independent on which is the last number, at the end just sum over all k. The complexity would be O(n^2 m).
public static long p(final long n, final long m) {
System.out.println("n=" + n + ", m=" + m);
return p(n, 1, m);
}
private static long p(final long n, final long digitFrom, final long m) {
final long digitTo = n - m + 1;
if (digitFrom > digitTo) return 0;
if (m == 1) return 1;
long sum = 0;
for (long firstDigit = digitFrom; firstDigit <= digitTo; firstDigit++)
sum += p(n - firstDigit, firstDigit, m - 1);
return sum;
}
Example debug:
n=6, m=3
1+1+4
1+2+3
2+2+2
From debug version:
public static long p(final long n, final long m) {
System.out.println("n=" + n + ", m=" + m);
return p(n, 1, m, new Stack<String>());
}
private static long p(final long n, final long digitFrom, final long m, Stack<String> digitStack) {
final long digitTo = n - m + 1;
if (digitFrom > digitTo) return 0;
if (m == 1) {
digitStack.push(n + "");
printStack(digitStack);
digitStack.pop();
System.out.println();
return 1;
}
long sum = 0;
for (long firstDigit = digitFrom; firstDigit <= digitTo; firstDigit++) {
digitStack.push(firstDigit + "+");
sum += p(n - firstDigit, firstDigit, m - 1, digitStack);
digitStack.pop();
}
return sum;
}
6, 5 + 1, 4 + 2, 4 + 1 + 1 and so on. –
Pluviometer Since you know how many digits you are to use I believe you can do this.
First of you can do this by repeatedly doing partition(n, 2). If you want n = 3, m = 3 you can just do partition(n, 2), and then for each of the answers you do partition(k, 2).
Example:
partition(6, 3):
partition(6, 2):
5 + 1, 4 + 2, 3 + 3, 2 + 4, 5 + 1
partition(5, 2):
4 + 1, 3 + 2 ...
Then you just add all of them together:
(4+1) + 1, (3+2)+1, (2+3)+1, (1+4)+1, (3+1)+2...
and sort them (largest number first).
4+1+1, 4+1+1...
Then you can just remove all the duplicates
Partition(n, 2) will run in O(n) (since you just need to loop up to n and do x + (n-x)). The number of times you will have to do this is O(m) of some kind. And sorting can be done in n (since you know it's all whole numbers). So I think this will run in O(n*m), which isn't good but it might be usable for you (if n or m is reasonably small).
You can first prepare sequences of summands, and then sequentially process them in pairs, step by step getting the Cartesian product.
As a sequence of summands you can use TreeMap<int[]> with a comparator that compares the contents of two sorted arrays to get rid of duplicate combinations such that 4+2 and 2+4. If you want to keep these combinations, you can use a 2D array int[][] instead. This simplifies the code a bit, but requires more computation time.
If n = 6, then the sequences of summands are as follows:
1: [1][2][3][4][5][6]
2: [1][2][3][4][5]
3: [1][2][3][4]
4: [1][2][3]
5: [1][2]
6: [1]
The reduce method passes through 5 stages, sequentially obtaining the Cartesian product:
1: [1][2][3][4][5][6]
2: [1][2][3][4][5]
---
sum1: [1,1][1,2][1,3]...[2,1][2,2][2,3]...
3: [1][2][3][4]
---
sum2: [1,1,1][1,2,1]...[2,1,1][2,2,1]...[3,1,1][3,2,1]...
4: [1][2][3]
---
sum3: [1,1,1,1]...[2,1,1,1]...[3,1,1,1]...
5: [1][2]
---
sum4: [1,1,1,1,1]...[2,1,1,1,1]...
6: [1]
---
total: [1,1,1,1,1,1]...
At each step of reduction, those combinations of summands that are greater than the specified number are excluded from the next step and as a consequence from the final result, and those combinations that have reached the specified number do not increase anymore.
int n = 6, m = 2; // n - sum, m - number of summands
Set<int[]> partition = IntStream.range(0, n)
// prepare sets of arrays of summands
.mapToObj(i -> IntStream.rangeClosed(1, n - i)
.mapToObj(j -> new int[]{j})
// Stream<TreeSet<int[]>>
.collect(Collectors.toCollection(
// comparing the contents of two arrays
() -> new TreeSet<>(Arrays::compare))))
// sequential summation of pairs of sets
.reduce((set1, set2) -> set1.stream()
// combinations of inner arrays
.flatMap(arr1 -> {
// sum of the elements of the first array
int sum = Arrays.stream(arr1).sum();
// if the specified number is reached
if (sum == n) // and the number of summands is reached
if (arr1.length == m) // don't increase this combination
return Arrays.stream(new int[][]{arr1});
else return Stream.empty(); // drop this combination
// otherwise continue appending summands
return set2.stream() // drop the combinations that are greater
.filter(arr2 -> Arrays.stream(arr2).sum() + sum <= n)
.map(arr2 -> Stream.of(arr1, arr2)
.flatMapToInt(Arrays::stream)
.sorted().toArray()) // the sorted array
// drop too long combinations
.filter(arr2 -> arr2.length <= m);
}) // set of arrays of combinations
.collect(Collectors.toCollection( // two arrays that differ
// only in order are considered the same partition
() -> new TreeSet<>(Arrays::compare))))
// otherwise an empty set of arrays
.orElse(new TreeSet<>(Arrays::compare));
// output, the integer partition with restricted number of summands
partition.stream().map(Arrays::toString).forEach(System.out::println);
Output:
[1, 5]
[2, 4]
[3, 3]
See also: Building permutation that sums to a number efficiently
this problem seems to be SubSet Sum Problem
its an NP problem meaning all the solutions would be non-deterministic (i.e. there isn't any known efficient algorithm).
you can however try some heuristic approach and find some satisfying results in a more efficient way.
© 2022 - 2024 — McMap. All rights reserved.