What would be the simplest solution to draw sine waves in SVG? I guess sine waves should be repeated in a simple loop with JavaScript... :)
Here are the X-Y coordinates as a good start... :)
http://jsbin.com/adaxuy/1/edit
<svg>
<line x1="0" y1="250" x2="500" y2="250"
style="stroke:black;stroke-width:1"/>
<line x1="250" y1="0" x2="250" y2="500"
style="stroke:black;stroke-width:1"/>
</svg>
Here is a proof of concept that adds multiple line elements to the SVG element:
var svg = document.getElementById('sine_wave').children[0];
var origin = { //origin of axes
x: 100,
y: 100
};
var amplitude = 10; // wave amplitude
var rarity = 1; // point spacing
var freq = 0.1; // angular frequency
var phase = 0; // phase angle
for (var i = -100; i < 1000; i++) {
var line = document.createElementNS("http://www.w3.org/2000/svg", "line");
line.setAttribute('x1', (i - 1) * rarity + origin.x);
line.setAttribute('y1', Math.sin(freq*(i - 1 + phase)) * amplitude + origin.y);
line.setAttribute('x2', i * rarity + origin.x);
line.setAttribute('y2', Math.sin(freq*(i + phase)) * amplitude + origin.y);
line.setAttribute('style', "stroke:black;stroke-width:1");
svg.appendChild(line);
}html, body, div{
height:100%;
}<div id="sine_wave">
<svg width="1000" height="1000">
<line x1="100" y1="0" x2="100" y2="200"
style="stroke:black;stroke-width:1"/>
<line x1="0" y1="100" x2="1000" y2="100"
style="stroke:black;stroke-width:1"/>
</svg>
</div>line elements too.) Thanks again! –
Rosefish An alternative to straight-line approximations would be a Bézier approximation. A pretty good approximation of the first quarter of one period is a cubic Bézier curve with the following control points:
0 0
1/2 1/2
1 1
π/2 1
Edit: Even more exact approximations are possible with the following control points:
0 0
0.512286623256592433 0.512286623256592433
1.002313685767898599 1
1.570796326794896619 1
(See NominalAnimal's explanations in the comments)
Demo comparing line elements (gray) and "good" Bézier (red) and "better" Bézier (green).
An approximation that exactly interpolates the slope and curvature in the spline's endpoints is
0 0
(6−(3/2π−3)²)/6 (6−(3/2π−3)²)/6
1 1
π/2 1
0, 0, 0.512286623256592433,0.512286623256592433, 1.002313685767898599,1, 1.570796326794896619,1 for the first quarter-period of the sine wave. @broofa: note that this is a cubic Bézier, not a quadratic one, and that Béziers often render faster and smoother than a similar polyline. –
Equate x[n], y[n], x[n]*2/3+x[n+1]/3, y[n]+dy[n]*(x[n+1]-x[n])/3, x[n]/3+x[n+1]*2/3, y[n+1]-dy[n+1]*(x[n+1]-x[n])/3, and x[n+1], y[n+1], where x[n] are the sampling points, y[n] = f(x[n]) (ie. f at x[n]), and dy[n] = d(f(t)/dt)[t=x[n]] (ie. derivative or slope of f at x[n]). Optimum curves are harder to find, but this yields an acceptable piecewise cubic approximation. –
Equate 0,0 0.51128733,0.51128733 1,1 π/2,1. They are optimal in the sense that the Bézier spline interpolates the slope and curvature exactly in the start/end points. –
Kath x[n] does not need to be regular. If you write code to fit a C2-continuous Bézier spline to a function, most of the code will usually be to find the best set of x[n]; they have the greatest impact on the result. –
Equate Here is a proof of concept that adds multiple line elements to the SVG element:
var svg = document.getElementById('sine_wave').children[0];
var origin = { //origin of axes
x: 100,
y: 100
};
var amplitude = 10; // wave amplitude
var rarity = 1; // point spacing
var freq = 0.1; // angular frequency
var phase = 0; // phase angle
for (var i = -100; i < 1000; i++) {
var line = document.createElementNS("http://www.w3.org/2000/svg", "line");
line.setAttribute('x1', (i - 1) * rarity + origin.x);
line.setAttribute('y1', Math.sin(freq*(i - 1 + phase)) * amplitude + origin.y);
line.setAttribute('x2', i * rarity + origin.x);
line.setAttribute('y2', Math.sin(freq*(i + phase)) * amplitude + origin.y);
line.setAttribute('style', "stroke:black;stroke-width:1");
svg.appendChild(line);
}html, body, div{
height:100%;
}<div id="sine_wave">
<svg width="1000" height="1000">
<line x1="100" y1="0" x2="100" y2="200"
style="stroke:black;stroke-width:1"/>
<line x1="0" y1="100" x2="1000" y2="100"
style="stroke:black;stroke-width:1"/>
</svg>
</div>line elements too.) Thanks again! –
Rosefish The following will add a one-cycle sine wave to your SVG graph:
const XMAX = 500;
const YMAX = 100;
// Create path instructions
const path = [];
for (let x = 0; x <= XMAX; x++) {
const angle = (x / XMAX) * Math.PI * 2; // angle = 0 -> 2π
const y = Math.sin(angle) * (YMAX / 2) + (YMAX / 2);
// M = move to, L = line to
path.push((x == 0 ? 'M' : 'L') + x.toFixed(2) + ',' + y.toFixed(2));
}
// Create PATH element
const pathEl = document.createElementNS("http://www.w3.org/2000/svg", "path");
pathEl.setAttribute('d', path.join(' ') );
pathEl.style.stroke = 'blue';
pathEl.style.fill = 'none';
// Add it to svg element
document.querySelector('svg').appendChild(pathEl);<svg width="500" height="100"/>This uses a PATH element made up of 'lineto' (straight line) commands. This works because, not surprisingly, it contains many (500) small line segments. You could simplify the path to have fewer points by using bezier curves to draw the segments, but this complicates the code. And you asked for simple. :)
Math.sin(angle) to Math.sin(angle * X), where X = number of cycles. Also, IMHO, a single path element (as above) is a more elegant solution than @Asad's many-line element answer, for several several reasons. 1. A path only adds a single DOM element. This improves performance of DOM layout and canvas rendering (important for animation) and a path can be 'fill'ed in the event you want to fill the area under your line. You can't fill separate line segments. –
Kujawa i var. thx. –
Kujawa for loop to take count of the number of cycles i.e for (var x = 0; x <= (XMAX * cylces); x++) { –
Andersen In case it is useful to anybody: Here is a one-liner SVG that closely approximates half of a sine wave using a cubic bezier approximation.
<svg width="100px" height="100px" viewBox="0 0 100 100">
<path stroke="#000000" fill="none" d="M0,0 C36.42,0,63.58,100,100,100" />
</svg>
I fitted the parameter 36.42 by minimizing the sum-squared (l2) distance between the bezier curve and the true cosine curve. https://octave-online.net/bucket~AN33qHTHk7eARgoSe7xpYg
My answer is based in part on How to approximate a half-cosine curve with bezier paths in SVG?
<path d="M0,0 c1.29,1.334 1.8516,1.334 3.1416,0" stroke-width=".1" /> –
Kohn For use in illustrations, this approximation works well.
<path d="M0,10 q5,20,10,0 t 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10,0" stroke="black" fill="none"/>
It's compact, relatively easy to work work with.
M0,10
q5,20,10,0
t 10 0
I find this useful for illustrating modulation in data communication. To illustrate AM (or even QAM), just repeat the q command with the new parameters. You may need to adjust the M command to shift it into view if you increase the amplitude
To use this in HTML5, just put it in an svg element
<h1>FM and QAM Examples</h1>
<svg>
<path d="
M0,20
q 5 20 10 0 t 10 0 10 0 10 0 10 0
7.5 0 5 0 5 0 5 0 5 0 5 0 5 0 7.5 0
10 0 10 0 10 0 10 0 10 0 10 0
10 0 10 0 10 0 10 0 10 0 10 0
M0,60
q 5 20 10 0 t 10 0 10 0 10 0 10 0
q 5 20 10 0 t 10 0 10 0 10 0 10 0
q 5 40 10 0 t 10 0 10 0 10 0 10 0
q 5 -20 10 0 t 10 0 10 0 10 0 10 0 10
" stroke="black" fill="none"/>
</svg>
Loop over the X axis and for each iteration compute the Y position using a sine function on the current X value.
Here's a CDMA illustration where I've used cubic splines for illustrating CDMA concepts. First define these functions:
<script>
function go(x,y) {return(`M ${x},${y}`)}
function to(y) {return(`c 5 0 5 ${y} 10 ${y}`)}
function dn(y=10) {return to(y)}
function up(y=10) {return to(-y)}
function path(d,color='black') {return `<path d="${d}" stroke=${color} fill="none"/>`}
function svg(t) {return `<svg>${t}</svg>`}
function bits(n) {
let s='', n0=(n>>1)
for (m=0x80;m;m>>=1) s+= up(10* (!(m&n0)-!(m&n)) )
return s;
}
function plot(a) {
let s='', y0=0
for (let y of a) {
s += up(y-y0); y0=y
}
return s
}
function add(a) {
let s=''
if typeof y0 == 'undefined' var y0=0
for (m=0x80;m;m>>=1) {
let y=0; for (let e of a) y+= 5-10*!(e&m)
s += up(y-y0); y0=y
}
return s
}
</script>
Then you can roughly illustrate waves like this:
<script>
document.write(svg(path(go(0,25)+(up()+dn()).repeat(10))))
</script>
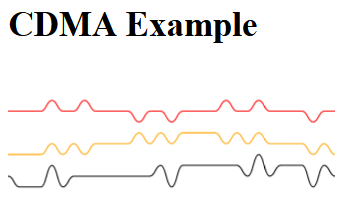
Here's an illustration of CDMA using this technique
<h1>CDMA Example</h1>
<script>
a=0b00010010
b=0b00010101
document.write(svg(
path(go(0,40)+bits(a)+bits(~a)+bits(a)+bits(~a)+bits(a),'red')+
path(go(0,80)+bits(b)+bits(b)+bits(~b)+bits(~b)+bits(~b),'orange')+
path(go(0,100+add([a,b])+add([~a,b])+add([a,~b])+add([~a,~b])+add([a,b])+add([~a,~b])))
))
</script>
NOTE: actual CDMA signals would not be bit-aligned or even chip-aligned
You can also use Bézier curves:
<path d="M0,50 Q50,100 100,50 T200,50 T300,50 T400,50 " fill="blue" />
M0,50 starts the path then Q draws a quadratic Bézier curve through the previous point and up to 100,50, using the guide point 100,50. after that T200,50 draws a smooth quadratic Bézier curve from the last point to 200,50. it resembles the previous guide point forward. I use two more T curves to create further cycles.
© 2022 - 2024 — McMap. All rights reserved.
<path>element in the document – Forgotten