The algorithm to find the point of intersection of two 3D line segment

Question

Finding the point of intersection for two 2D line segments is easy; the formula is straight forward. But finding the point of intersection for two 3D line segments is not, I afraid.

What is the algorithm, in C# preferably that finds the point of intersection of two 3D line segments?

I found a C++ implementation here. But I don't trust the solution because it makes preference of a certain plane (look at the way perp is implemented under the implementation section, it assumes a preference for z plane. Any generic algorithm must not assume any plane orientation or preference).

Is there a better solution?

Gasparo

You might find it useful to take a look at a corresponding article in Wikipedia - it does not have a code, but the algorithm is described pretty well, imho (but you should know some math anyway). en.wikipedia.org/wiki/Bentley%e2%80%93Ottmann_algorithm Update: funny enough is that Russian version of the same Wikipedia entry contains more details (and formular) and an algorithm description is pseudo-code as well. Here's a link to translation of this entry to English (via Google Translate): translate.google.com/… – Glendoraglendower

I like the math in your answer, but I don't think your statement about a generic algorithm is true. Projecting the lines onto the xy-plane will turn the problem into a 2d problem. Then, find the intersection of the resulting points/lines and test its validity. Choosing z is just an implementation convenience. Working in a lower dimension might reduce the operation count, too. – Photomontage

@Derek, I'm not sure whether projecting lines onto the xy-plane is a good idea. Consider this assuming there are two x-y lines, each located on different z planes. If you project them to the xy planes then they will appear to be intersecting, even though they are not. – Gasparo

Soon Hui, Yes, that is correct. After determining the intersection in the xy-plane, you would need to test its validity. This is just a matter of "plugging the numbers back in". The upside is if the numbers don't check, then you can conclude that the lines don't intersect. Note: you would need to handle a couple of special cases (one line is directed along z-hat, parallel lines). On a related note, the solution you posted below assumes that the lines are infinite. You would need to do a validation test on that solution, as well. – Photomontage

@Derek, my solution would be easier and cleaner to implement because I just need to check for a and b must be between 0 and 1 – Gasparo

@DerekE - NO. I'm afraid you are wrong. Projecting into a 2-d plane can easily fail, even when a solution does exist. Consider two line segments, at least one of which is parallel to the z axis. Now the projection will be a point. – Siliceous

This was some time ago and I believe I was mistakenly talking about infinite lines. Other comments seem to have missed the part where I said to verify the projected intersection. This procedure will fail for two finite segments end on end that project to points and that don't intersect, as woodchips hinted at. I apologize. But if its infinite lines, I think my statement is correct. Also note that my comment was not meant to be an efficient algorithm, just a counter-example. – Photomontage

Btw the problem can be simplified if the 3rd dimension is removed. In some cases you can work with just the projects of both 3D lines on the same plane thus reducing the problem to its 2D dimensional equivalent. – Nictitate

Answer 1

I found a solution: it's here.

The idea is to make use of vector algebra, to use the dot and cross to simply the question until this stage:

a (V1 X V2) = (P2 - P1) X V2

and calculate the a.

Note that this implementation doesn't need to have any planes or axis as reference.

Gasparo

Hello, i used the solution you presented, but sometimes i get mirrored results... you had this problem too? – Tullus

@DanielaMorais, I would not have accepted my own answer against my own question if it didn't work – Gasparo

For anyone else that finds this, you need to take the magnitude of each side. if ( |(V1 X V2)| != 0 ) a = |(P2-P1) X V2| / |V1 X V2| 'a' would be your t value. – Clementia

If | V1 X V2 | is zero, they aren't coplanar. Neat. – Eolanda

There are problems with this answer. This solution gives false positives – Keramic

There is problems with this answer. You may get mirrored result. Here is my correction to the solution https://mcmap.net/q/491371/-the-algorithm-to-find-the-point-of-intersection-of-two-3d-line-segment – Annalisaannalise

Answer 2

Most 3D lines do not intersect. A reliable method is to find the shortest line between two 3D lines. If the shortest line has a length of zero (or distance less than whatever tolerance you specify) then you know that the two original lines intersect.

A method for finding the shortest line between two 3D lines, written by Paul Bourke is summarized / paraphrased as follows:

In what follows a line will be defined by two points lying on it, a point on line "a" defined by points P1 and P2 has an equation

Pa = P1 + mua (P2 - P1)

similarly a point on a second line "b" defined by points P3 and P4 will be written as

Pb = P3 + mub (P4 - P3)

The values of mua and mub range from negative to positive infinity. The line segments between P1 P2 and P3 P4 have their corresponding mu between 0 and 1.

There are two approaches to finding the shortest line segment between lines "a" and "b".

Approach one:

The first is to write down the length of the line segment joining the two lines and then find the minimum. That is, minimise the following

|| Pb - Pa ||^2

Substituting the equations of the lines gives

|| P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ||^2

The above can then be expanded out in the (x,y,z) components.

There are conditions to be met at the minimum, the derivative with respect to mua and mub must be zero. ...the above function only has one minima and no other minima or maxima. These two equations can then be solved for mua and mub, the actual intersection points found by substituting the values of mu into the original equations of the line.

Approach two:

An alternative approach but one that gives the exact same equations is to realise that the shortest line segment between the two lines will be perpendicular to the two lines. This allows us to write two equations for the dot product as

(Pa - Pb) dot (P2 - P1) = 0
(Pa - Pb) dot (P4 - P3) = 0

Expanding these given the equation of the lines

( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P2 - P1) = 0
( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P4 - P3) = 0

Expanding these in terms of the coordinates (x,y,z) ... the result is as follows

d1321 + mua d2121 - mub d4321 = 0
d1343 + mua d4321 - mub d4343 = 0

where

dmnop = (xm - xn)(xo - xp) + (ym - yn)(yo - yp) + (zm - zn)(zo - zp)

Note that dmnop = dopmn

Finally, solving for mua gives

mua = ( d1343 d4321 - d1321 d4343 ) / ( d2121 d4343 - d4321 d4321 )

and back-substituting gives mub

mub = ( d1343 + mua d4321 ) / d4343

This method was found on Paul Bourke's website which is an excellent geometry resource. The site has been reorganized, so scroll down to find the topic.

Cyclostome

While this is true one might want to approximate the intersection in 3D space. Just like comparing two floats and saying one is equal to the other depending on some epsilon factor that defines an interval (and not a single value) of equality. Another solution (if possible depending on the case) is to dump the 3rd dimension (setting it to a constant such as 0) and go only with two of the coordinates thus using the projections and not the lines themselves. Still +1 for addressing the issue. – Nictitate

What are mua, mub, d1321 and so on? A line segment is usually defined with two vectors. – Nutter

Can't understand what d1321 dmnop stands for. – Introduction

After read this version code paulbourke.net/geometry/pointlineplane/calclineline.cs, understand that d1321 maybe dot((p1-p3),(p2-p1)). – Introduction

Isn't this just for infinite Lines, not Line Segments that the OP was asking for? – Durward

After finding Pa and Pb you can check whether the points are within the line segments and use the results appropriate to the application. – Cyclostome

@DougFerguson hey Doug I appreciate the answer, but it's super difficult to understand what d2121 etc means? – Hickson

@Hickson StayOnTarget was very helpful to add the summary. Paul Bourke's website is the best reference since the formatting is better and has sample code. However that website may change or disappear. gonnavis made a good observation in his Sep 27, 2020 comment. Thus d2121 = p21.X * p21.X + p21.Y * p21.Y + p21.Z * p21.Z where p21 = p2 - p1 – Cyclostome

Answer 3

// This code in C++ works for me in 2d and 3d

// assume Coord has members x(), y() and z() and supports arithmetic operations
// that is Coord u + Coord v = u.x() + v.x(), u.y() + v.y(), u.z() + v.z()

inline Point
dot(const Coord& u, const Coord& v) 
{
return u.x() * v.x() + u.y() * v.y() + u.z() * v.z();   
}

inline Point
norm2( const Coord& v )
{
return v.x() * v.x() + v.y() * v.y() + v.z() * v.z();
}

inline Point
norm( const Coord& v ) 
{
return sqrt(norm2(v));
}

inline
Coord
cross( const Coord& b, const Coord& c) // cross product
{
return Coord(b.y() * c.z() - c.y() * b.z(), b.z() * c.x() - c.z() * b.x(), b.x() *  c.y() - c.x() * b.y());
}

bool 
intersection(const Line& a, const Line& b, Coord& ip)
// http://mathworld.wolfram.com/Line-LineIntersection.html
// in 3d; will also work in 2d if z components are 0
{
Coord da = a.second - a.first; 
Coord db = b.second - b.first;
    Coord dc = b.first - a.first;

if (dot(dc, cross(da,db)) != 0.0) // lines are not coplanar
    return false;

Point s = dot(cross(dc,db),cross(da,db)) / norm2(cross(da,db));
if (s >= 0.0 && s <= 1.0)
{
    ip = a.first + da * Coord(s,s,s);
    return true;
}

return false;
}

Policeman

Answer 4

I tried @Bill answer and it actually does not work every time, which I can explain. Based on the link in his code.Let's have for example these two line segments AB and CD.

A=(2,1,5), B=(1,2,5) and C=(2,1,3) and D=(2,1,2)

when you try to get the intersection it might tell you It's the point A (incorrect) or there is no intersection (correct). Depending on the order you put those segments in.

x = A+(B-A)s
x = C+(D-C)t

Bill solved for s but never solved t. And since you want that intersection point to be on both line segments both s and t have to be from interval <0,1>. What actually happens in my example is that only s if from that interval and t is -2. A lies on line defined by C and D, but not on line segment CD.

var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

where da is B-A, db is D-C and dc is C-A, I just preserved names provided by Bill.

Then as I said you have to check if both s and t are from <0,1> and you can calculate the result. Based on formula above.

if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
   Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}

Also another problem with Bills answer is when two lines are collinear and there is more than one intersection point. There would be division by zero. You want to avoid that.

Verbalism

Answer 5

The original source you mention is only for the 2d case. The implementation for perp is fine. The use of x and y are just variables not an indication of preference for a specific plane.

The same site has this for the 3d case: "http://geomalgorithms.com/a07-_distance.html"

Looks like Eberly authored a response: "https://www.geometrictools.com/Documentation/DistanceLine3Line3.pdf"

Putting this stuff here because google points to geomalgorithms and to this post.

Hesper

Answer 6

But finding the point of intersection for two 3D line segment is not, I afraid.

I think it is. You can find the point of intersection in exactly the same way as in 2d (or any other dimension). The only difference is, that the resulting system of linear equations is more likely to have no solution (meaning the lines do not intersect).

You can solve the general equations by hand and just use your solution, or solve it programmatically, using e.g. Gaussian elemination.

Beulahbeuthel

If we extend the 2D way of doing things, you will have three equations (x,y and z) for two unknowns (u,v). It is definitely nontrivial to solve it. – Gasparo

Well... as trivial as the 2d case. You could just use the first two equations to determine u and v, and then check if the last equation holds with these values for u and v. If it does, you have found your intersection. If it does not, the lines do not intersect. I do not see any difficulty here. – Beulahbeuthel

In Linear Algebra, this is considered trivial. For an algorithm some care must be taken, though. For example, if the two lines both lived in the x=0, y=0 or z=0 plane, one of those three equations will not give you any information. (Assuming the equations are some_point_on_line_1 = some_point_on_line_2) – Photomontage

@Derek, that's something I strive to avoid by having a generic solution; I don't want to check the edge cases all over my code. – Gasparo

@DerekE Also look out for this when optimizing your code, a library I used had this problem because it was optimized too aggressively. – Norry

Answer 7

I found an answer!

in an answer from above, I found these equations:

Eq#1: var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

Eq#2: var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

Then I modified #3rd Equation:

Eq#3:

if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
   Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}

And while keeping Eq#1 and Eq#2 just the same, I created this equations:

MyEq#1: Vector3f p0 = da.mul(s).add(A<vector>); MyEq#2: Vector3f p1 = db.mul(t).add(C<vector>);

then I took a wild guess at creating these three more equations:

MyEq#3: Vector3f p0z = projUV(da, p0).add(A<vector>); MyEq#4: Vector3f p1z = projUV(db, p1).add(C<vector>);

and finally to get the subtraction of the two magnitudes of the projUV(1, 2) gives you the margin of the error between 0 and 0.001f to find whether the two lines intersect.

MyEq#5: var m = p0z.magnitude() - p1z.magnitude();

Now I mind you, this was done in Java. This explanation is not java convention ready. Just put it to work from the above equations. (Tip: Don't transform to World Space yet so that both projection of UV equations fall exactly where you want them).

And these equations are visually correct in my program.

Interfaith

Can you post a complete code sample? It's hard to evaluate your claim – Gasparo

sorry but I cannot explain it, or write a code to simply this example, but here is my video where I capture the lines intersecting from the modified example above: youtube.com/watch?v=yDVS4mH7dFA Just a quick reminder, the line segment that touches the other two lines, it is only a representation of the closes point to the two line, and that's why it cycles between the top and the bottom, because at those points, the end and start tips are closest to each other. Enjoy. – Interfaith

Answer 8

In addition to Bobs answer:

I find on testing that the intersection() function as written solves half the original problem, which was an algorithm to find the point of intersection of two 3D line segments.

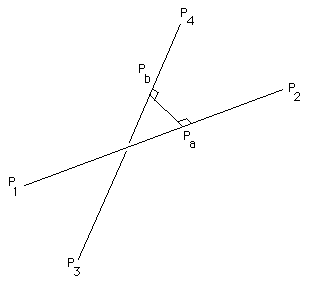
Assuming the lines are coplanar, there are 5 possible outcomes to this question:

1. The line segments are parallel, so they don't intersect, or,

2. The line segments aren't parallel, and the infinite length lines they lie upon do intersect, but the intersection point is not within the bounds of either line segment, or,

3. The lines intersect and the intersection point is within the bounds of line a but not line b, or,

4. The lines intersect and the intersection point is within the bounds of line b but not line a, or,

5. The lines intersect and the intersection point is within the bounds of both line segments.

Bob's intersection() function returns true when the lines intersect and the point of intersection is within the bounds of line a, but returns false if the lines intersect and the point of intersection is within the bounds of only line b.

But if you call intersect() twice, first with lines a then b and then a second time with lines b and a (first and second params swapped), then if both calls return true, then the intersect is contained within both line segments (case 5). If both calls return false, then neither line segment contains the intersect (case 2). If only one of the calls returns true, then the segment passed as the first parameter on that call contains the point of intersection (cases 3 or 4).

Also, if the return from the call to norm2(cross(da,db)) equals 0.0, then the line segments are parallel (case 1).

The other thing I noted in testing is that with fixed precision floating point numbers of the kind code is often implemented with, it can be quite unusual for dot(dc, cross(da,db)) to return 0.0, so returning false when its not the case might not be what you want. You might want to introduce a threshold below which the code continues to execute rather than return false. This indicates the line segments are skew in 3D, but depending on your application you might want to tolerate a small amount of skew.

The final thing I noticed was this statement in Bill's code:

ip = a.first + da * Coord(s,s,s);

That da * Coord(s,s,s) looks to be a vector times vector multiply. When I replaced it with a scalar multiple of da * s, I found it worked fine.

But in any case, many thanks to Bob. He figured out the hard part.

Cordell

Answer 9

https://bloodstrawberry.tistory.com/1037 This blog was implemented by Unity c#.

Vector3 getContactPoint(Vector3 normal, Vector3 planeDot, Vector3 A, Vector3 B)
{
    Vector3 nAB = (B - A).normalized;

    return A + nAB * Vector3.Dot(normal, planeDot - A) / Vector3.Dot(normal, nAB);
}

(Vector3 point1, Vector3 point2) getShortestPath(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
    Vector3 AB = A - B;
    Vector3 CD = C - D;
    Vector3 line = Vector3.Cross(AB, CD);
    Vector3 crossLineAB = Vector3.Cross(line, AB);
    Vector3 crossLineCD = Vector3.Cross(line, CD);

    return (getContactPoint(crossLineAB, A, C, D), getContactPoint(crossLineCD, C, A, B));
}

Joinery

Answer 10

I would start by treating the corresponding line-line intersect problem. Say the first line goes through point p1 and is parallel to vector v1, while the second line goes through point p2 and is parallel to vector v2. As some have already noted, in 3D rarely do two lines intersect. But if we assume that they do, then the intersection point q can be written as

q = p2 + t * v2

where

t = dot(p1 - p2, v3) / dot(v2, v3)

and where

v3 = cross(cross(v1, v2), v1).

Since we are assuming the two lines intersect, they lie in the same plane. The vector found by taking the cross product of v1 and v2 is orthogonal to this plane. Taking the next cross product with v1 places v3 back in the plane but also orthogonally to v1. The 3D problem can then be treated as a 2D problem, leading to the expression for t.

Having a solution to the line-line intersect problem, the segment-segment intersection problem is now simply a matter of checking if q lies on both segments. It should just be a matter of comparing dot products to tell if q lies on the first segment. The second segment is even easier to check since the expression above for q always places q on the second line, i.e., we just need to examine the value of t.

Adest