Should Feature Selection be done before Train-Test Split or after?

Question

Actually, there is a contradiction of 2 facts that are the possible answers to the question:

1. The conventional answer is to do it after splitting as there can be information leakage, if done before, from the Test-Set.

2. The contradicting answer is that, if only the Training Set chosen from the whole dataset is used for Feature Selection, then the feature selection or feature importance score orders is likely to be dynamically changed with change in random_state of the Train_Test_Split. And if the feature selection for any particular work changes, then no Generalization of Feature Importance can be done, which is not desirable. Secondly, if only Training Set is used for feature selection, then the test set may contain certain set of instances that defies/contradicts the feature selection done only on the Training Set as the overall historical data is not analyzed. Moreover, feature importance scores can only be evaluated when, given a set of instances rather than a single test/unknown instance.

Annisannissa

The title of this post is clear, but it's not clear what point 2. is saying. Will upvote if the second point can be rewritten to be more clear. – Pointless

Should this question not be closed, or archived? Because it is about ML methodology and not programming. Which I see many ML questions closed frequently about... – Note

Answer 1

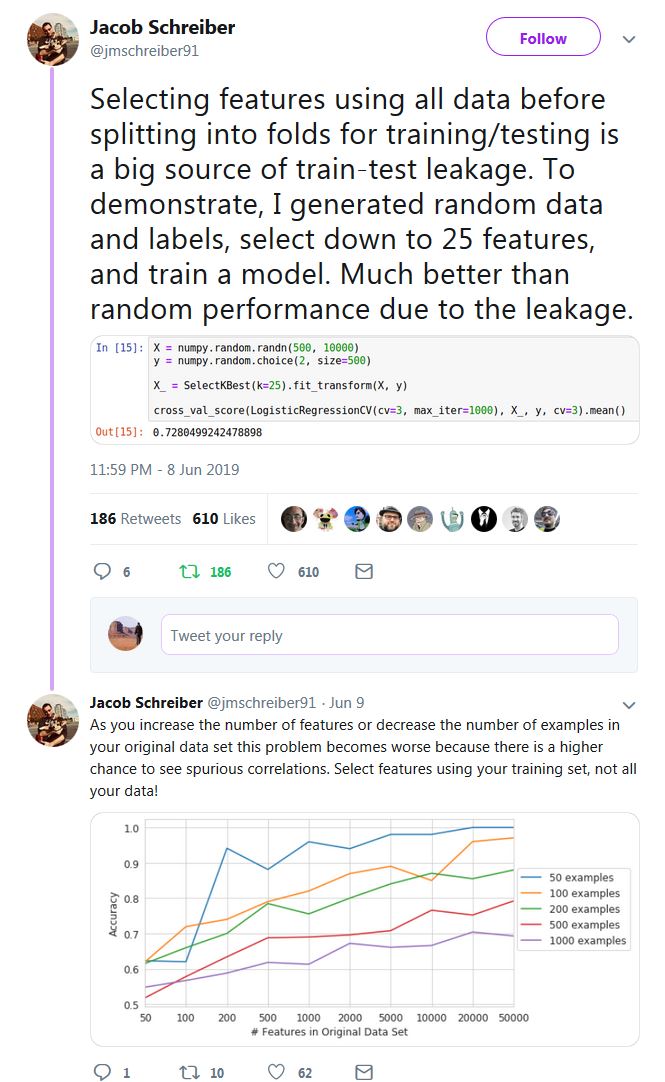
It is not actually difficult to demonstrate why using the whole dataset (i.e. before splitting to train/test) for selecting features can lead you astray. Here is one such demonstration using random dummy data with Python and scikit-learn:

import numpy as np
from sklearn.feature_selection import SelectKBest
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# random data:
X = np.random.randn(500, 10000)
y = np.random.choice(2, size=500)

Since our data X are random ones (500 samples, 10,000 features) and our labels y are binary, we expect than we should never be able to exceed the baseline accuracy for such a setting, i.e. ~ 0.5, or around 50%. Let's see what happens when we apply the wrong procedure of using the whole dataset for feature selection, before splitting:

selector = SelectKBest(k=25)
# first select features
X_selected = selector.fit_transform(X,y)
# then split
X_selected_train, X_selected_test, y_train, y_test = train_test_split(X_selected, y, test_size=0.25, random_state=42)

# fit a simple logistic regression
lr = LogisticRegression()
lr.fit(X_selected_train,y_train)

# predict on the test set and get the test accuracy:
y_pred = lr.predict(X_selected_test)
accuracy_score(y_test, y_pred)
# 0.76000000000000001

Wow! We get 76% test accuracy on a binary problem where, according to the very basic laws of statistics, we should be getting something very close to 50%! Someone to call the Nobel Prize committee, and fast...

... the truth of course is that we were able to get such a test accuracy simply because we have committed a very basic mistake: we mistakenly think that our test data is unseen, but in fact the test data have already been seen by the model building process during feature selection, in particular here:

X_selected = selector.fit_transform(X,y)

How badly off can we be in reality? Well, again it is not difficult to see: suppose that, after we have finished with our model and we have deployed it (expecting something similar to 76% accuracy in practice with new unseen data), we get some really new data:

X_new = np.random.randn(500, 10000)

where of course there is not any qualitative change, i.e. new trends or anything - these new data are generated by the very same underlying procedure. Suppose also we happen to know the true labels y, generated as above:

y_new = np.random.choice(2, size=500)

How will our model perform here, when faced with these really unseen data? Not difficult to check:

# select the same features in the new data
X_new_selected = selector.transform(X_new)
# predict and get the accuracy:
y_new_pred = lr.predict(X_new_selected)
accuracy_score(y_new, y_new_pred)
# 0.45200000000000001

Well, it's true: we sent our model to the battle, thinking that it was capable of a ~ 76% accuracy, but in reality it performs just as a random guess...

---

So, let's see now the correct procedure (i.e. split first, and select the features based on the training set only):

# split first
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# then select features using the training set only
selector = SelectKBest(k=25)
X_train_selected = selector.fit_transform(X_train,y_train)

# fit again a simple logistic regression
lr.fit(X_train_selected,y_train)
# select the same features on the test set, predict, and get the test accuracy:
X_test_selected = selector.transform(X_test)
y_pred = lr.predict(X_test_selected)
accuracy_score(y_test, y_pred)
# 0.52800000000000002

Where the test accuracy 0f 0.528 is close enough to the theoretically predicted one of 0.5 in such a case (i.e. actually random guessing).

Kudos to Jacob Schreiber for providing the simple idea (check all the thread, it contains other useful examples), although in a slightly different context than the one you ask about here (cross-validation):

Anabantid

Answer 2

The conventional answer #1 is correct here; the arguments in the contradicting answer #2 do not actually hold.

When having such doubts, it is useful to imagine that you simply do not have any access in any test set during the model fitting process (which includes feature importance); you should treat the test set as literally unseen data (and, since unseen, they could not have been used for feature importance scores).

Hastie & Tibshirani have clearly argued long ago about the correct & wrong way to perform such processes; I have summarized the issue in a blog post, How NOT to perform feature selection! - and although the discussion is about cross-validation, it can be easily seen that the arguments hold for the case of train/test split, too.

The only argument that actually holds in your contradicting answer #2 is that

the overall historical data is not analyzed

Nevertheless, this is the necessary price to pay in order to have an independent test set for performance assessment, otherwise, with the same logic, we should use the test set for training, too, shouldn't we?

---

Wrap up: the test set is there solely for performance assessment of your model, and it should not be used in any stage of model building, including feature selection.

UPDATE (after comments):

the trends in the Test Set may be different

A standard (but often implicit) assumption here is that the training & test sets are qualitatively similar; it is exactly due to this assumption that we feel OK to just use simple random splits to get them. If we have reasons to believe that our data change in significant ways (not only between train & test, but during model deployment, too), the whole rationale breaks down, and completely different approaches are required.

Also, on doing so, there can be a high probability of Over-fitting

The only certain way of overfitting is to use the test set in any way during the pipeline (including for feature selection, as you suggest). Arguably, the linked blog post has enough arguments (including quotes & links) to be convincing. Classic example, the testimony in The Dangers of Overfitting or How to Drop 50 spots in 1 minute:

as the competition went on, I began to use much more feature selection and preprocessing. However, I made the classic mistake in my cross-validation method by not including this in the cross-validation folds (for more on this mistake, see this short description or section 7.10.2 in The Elements of Statistical Learning). This lead to increasingly optimistic cross-validation estimates.

As I have already said, although the discussion here is about cross-validation, it should not be difficult to convince yourself that it perfectly applies to the train/test case, too.

feature selection should be done in such a way that Model Performance is enhanced

Well, nobody can argue with this, of course! The catch is - which exact performance are we talking about? Because the Kaggler quoted above was indeed getting better "performance" as he was going along (applying a mistaken procedure), until his model was faced with real unseen data (the moment of truth!), and it unsurprisingly flopped.

Admittedly, this is not trivial stuff, and it may take some time until you internalize them (it's no coincidence that, as Hastie & Tibshirani demonstrate, there are even research papers where the procedure is performed wrongly). Until then, my advice to keep you safe, is: during all stages of model building (including feature selection), pretend that you don't have access to the test set at all, and that it becomes available only when you need to assess the performance of your final model.

Anabantid

If the feature selection is done by considering only the trend of the Training Set Instances, then it may not be just to impose that feature selection on the Test Set, as the trends in the Test Set may be different. Also, on doing so, there can be a high probability of Over-fitting. On the contrary, if the whole dataset is utilized just to select the important features and keeping the Model Training Process independent of the Test Set (untrained model initialized and then trained only using the Training Set with selected features), can help achieve a model with higher statistical potential. – Annisannissa

The utility of keeping a separate test set is to analyze the performance of the Model right? So, say a Machine Learning Model, M1 (Random Forest Classifier) is trained using the Training Set and based on the feature importance score, feature selection is done both on the Training Set and Test Set. Then another Machine Learning Model, M2 (AdaBoost Classifier) is trained with the Training Set and its performance is evaluated using the Test Set. So, what is the utility of the test set to the Trained Model M1, as we are not interested with the Performance Evaluation of Model M1...? – Annisannissa

To wrap up: Feature Selection and Model Performance should be independent of each other. In other words, based on Model Performance, Feature Selection is not aimed to be done. Rather, feature selection should be done in such a way that Model Performance is enhanced. – Annisannissa

Actually I'm not convinced about your argument on the Over-fitting which can occur if feature selection is done only on the Training Set and can be unavoidable at times. – Annisannissa

Another point is: Say I have a dataset, D. I want to perform some filtering either by deleting rows or columns in the dataset. Just filtering or Data Cleaning I e., like removing unwanted features...In that case, I can surely use the whole dataset for assessment? And after deleting some features, I can split the dataset and use a completely untrained model on the Training Set and validate on the test set. The untrained model has no info about the test set. In the Dataset Filtering step, I think there is no such Training Set or Test Set involved.... – Annisannissa

Actually Feature Selection is a step of Data Preparation as explained here, analyticsindiamag.com/… – Annisannissa

@NavoneelChakrabarty It is your right not to be convinced - just don't claim afterwards that you were not warned (the rest of your first comment is unintelligible - i have not said that). The post you have linked to is a very general one, and it certainly does not say that feature selection is not part of the model building process. – Anabantid

@NavoneelChakrabarty Extending the question ad infinitum with new examples and sub-cases is neither productive nor how SO works: you were presented with solid arguments, evidence, and advice by an SO user with an arguably good track record in ML; you can choose to ignore it at your own peril... – Anabantid

I find your behaviour extremely inappropriate on SO. You may have a good track record in ML but you are talking to a Research Composer having 8 Research Papers accepted at renowned International Conferences. Anyways AI had expected a healthy conversation with u....though failed!!! also link I shared proves that Feature Selection can be used as a part of Dataset Preparation. Good Luckj !!!! – Annisannissa

@NavoneelChakrabarty I'm both sorry and puzzled you feel that way; if you feel that providing such an answer (which took time, BTW) is "extremely inappropriate", or the conversation is "unhealthy", or if you consider "healthy" to ask while obviously knowing the answer already (again, not how SO works), we can just agree to disagree. No way of knowing your background (in contrast with mine, which is publicly shown), but if you really think that a blog post can constitute any type of "proof", then good luck indeed (I did use one, yes, but only as additional evidence, not primary one)... – Anabantid