Let's say you have a company and you want to create an inventory tool:
Be able to (efficiently) search products by name so you can update the stock.
Get, at any time, the product with the lowest items in stock, so that you are able to plan your next order.
One way to handle these requirements could be by using two different
data structures: one for efficient search by name, for instance, a
hash table, and a priority queue to get the item that most urgently
needs to be resupplied. You have to manage to coordinate those two
data structures and you will need more than twice memory. if we sort
the list of entries according to name, we need to scan the whole list
to find a given value for the other criterion, in this case, the
quantity in stock. Also, if we use a min-heap with the scarcer
products at its top, then we will need linear time to scan the whole
heap looking for a product to update.
Treap
Treap is the blend of tree and heap. The idea is to enforce BST’s
constraints on the names, and heap’s constraints on the quantities.
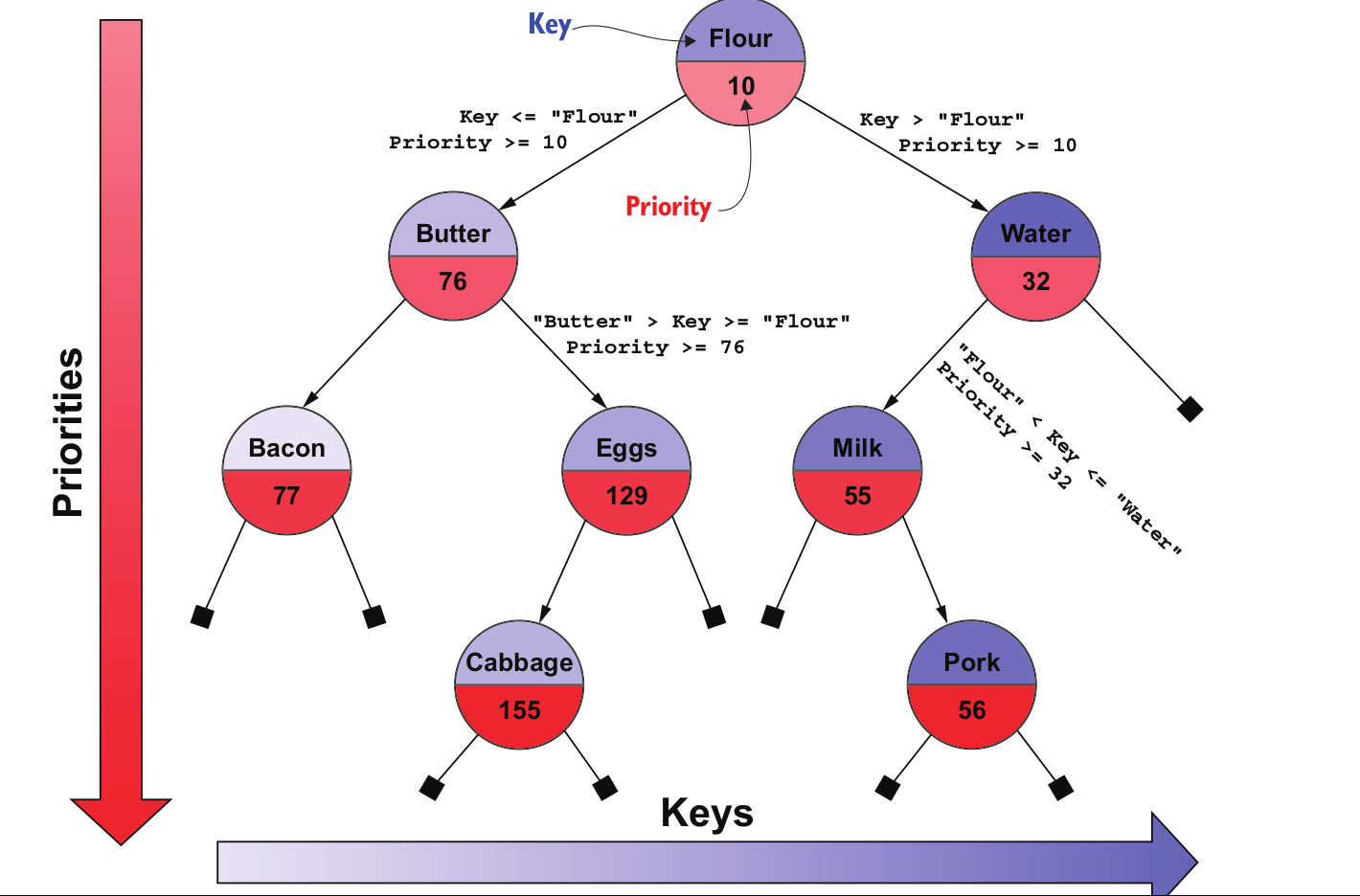
![enter image description here]()
Product names are treated as the keys of a binary search tree.
The inventory quantities, instead, are treated as priorities of a
heap, so they define a partial ordering from top to bottom. For
priorities, like all heaps, we have a partial ordering, meaning that
only nodes on the same path from the root to leaves are ordered with
respect to their priority. In the above image, you can see that
children nodes always have a higher stock count than their parents,
but there is no ordering between siblings.
Reference