Time complexity of node deletion in singly- and doubly-linked lists

Question

Why is the time complexity of node deletion in doubly linked lists (O(1)) faster than node deletion in singly linked lists (O(n))?

Upali

Answer 1

The problem assumes that the node to be deleted is known and a pointer to that node is available.

In order to delete a node and connect the previous and the next node together, you need to know their pointers. In a doubly-linked list, both pointers are available in the node that is to be deleted. The time complexity is constant in this case, i.e., O(1).

Whereas in a singly-linked list, the pointer to the previous node is unknown and can be found only by traversing the list from head until it reaches the node that has a next node pointer to the node that is to be deleted. The time complexity in this case is O(n).

In cases where the node to be deleted is known only by value, the list has to be searched and the time complexity becomes O(n) in both singly- and doubly-linked lists.

Bylaw

This is incorrect in regards to removing a node from a singly linked list requiring O(n) complexity - see my answer below. There is a trick where you copy the value from the next node from the one being removed and then skip that one to point to the node afterwards, thus eliminating any need to traverse the list. – Ebonieebonite

Answer 2

Actually deletion in singly linked lists can also be implemented in O(1).

Given a singly linked list with the following state:

SinglyLinkedList:
   Node 1 -> Node 2
   Node 2 -> Node 3
   Node 3 -> Node 4
   Node 4 -> None

   Head = Node 1

We can implement delete Node 2 in such a way:

Node 2 Value <- Node 3 Value
Node 2 -> Node 4

Here we replace the value of Node 2 with the value of its next node (Node 3) and set its next value pointer to the next value pointer of Node 3 (Node 4), skipping over the now effectively "duplicate" Node 3. Thus no traversal needed.

Ebonieebonite

Makes sense but won't really work when deleting the last element unless you have a reference to the previous (second to last) node . – Exodus

In that case @Exodus you just delete the node entirely so the previous node's reference will no longer point to anything. The specifics around GC etc will obviously depend upon the technology and implementation (e.g. you could use a weak reference). – Ebonieebonite

before trying to replace something you should go along the list and find the deleted node first. which is basically the same with going along the list until finding the predecessor of deleted node. actually your way involves an extra step forward so it is worse than the canonical O(n) way of doing it – Mindexpanding

@Mindexpanding That is incorrect. What you are describing is a search operation followed by a delete operation. Delete operations already know which node is to be deleted. If in doubt about time complexities of common data structures it's always good to refer to bigocheatsheet.com. – Ebonieebonite

well, ok, i didn't assume copying the data. copying is too expensive operation if the node has lots of data fields. ps. i'm surely not the one who needs a cheat sheet – Mindexpanding

You don't need to copy the data, you can have a reference (pointer) to the node, exactly like how nodes in a linked list point to the next node. – Ebonieebonite

Something to be aware of with this solution is that you're not freeing/deallocating Node 3. As the answer states, this leaves you with an effective "duplicate" (and disconnected) Node 3. This changes the space complexity from what is normally O(n) for singly linked lists. I'm not saying you can't "delete" nodes this way, but its definitely not standard practice and not without its drawbacks. – Unwatched

Answer 3

Because you can't look backwards...

Nobe

Answer 4

Insertion and deletion at a known position is O(1). However, finding that position is O(n), unless it is the head or tail of the list.

When we talk about insertion and deletion complexity, we generally assume we already know where that's going to occur.

Gripe

Answer 5

It has to do with the complexity of fixing up the next pointer in the node previous to the one you're deleting.

Seedtime

Answer 6

Unless the element to be deleted is the head(or first) node, we need to traverse to the node before the one to be deleted. Hence, in worst case, i.e., when we need to delete the last node, the pointer has to go all the way to the second last node thereby traversing (n-1) positions, which gives us a time complexity of O(n).

Ultraviolet

Answer 7

I don't think Its O(1) unless you know the address of the node whichh has to be deleted ..... Don't you loop to reach the node which has to be deleted from head ????

It is O(1) provided you have the address of the node which has to be deleted because you have it's prev node link and next node link . As you have all the necessary links available just make the "node of interest " out of the list by re arranging the links and then free() it .

But in a single linked list you have to traverse from head to get it's previous and next address doesn't matter whether you have the address to f the node to be deleted or the node position ( as in 1st ,2nd ,10th etc.,.) To be deleted .

Lepp

Answer 8

Suppose there is a linked list from 1 to 10 and you have to delete node 5 whose location is given to you.

1 -> 2 -> 3 -> 4 -> 5-> 6-> 7-> 8 -> 9 -> 10

You will have to connect the next pointer of 4 to 6 in order to delete 5.

1. Doubly Linked list You can use the previous pointer on 5 to go to 4. Then you can do

4->next = 5->next;

or

Node* temp = givenNode->prev;
temp->next = givenNode->next;

Time Complexity = O(1)

2. singly Linked List Since you don't have a previous pointer in Singly linked list you cant go backwards so you will have to traverse the list from head

Node* temp = head;
while(temp->next != givenNode)
{
  temp = temp->next;
}
temp->next = givenNode->next;

Time Complexity = O(N)

Errolerroll

Answer 9

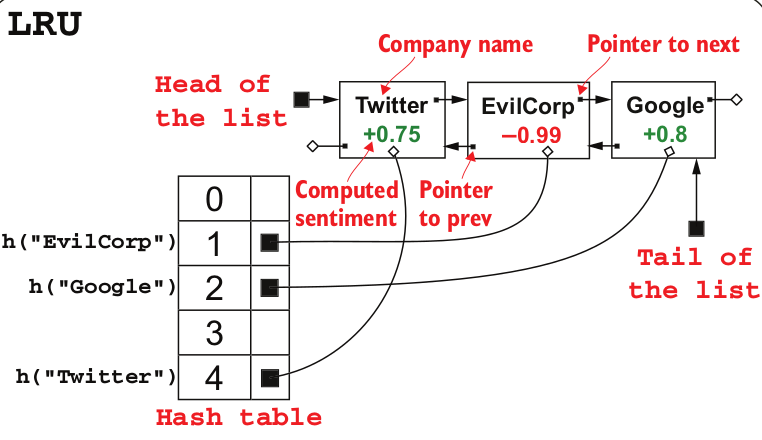
In LRU cache design, deletion in doubly linked list takes O(1) time. LRU cache is implemented with hash map and doubly linked list. In the doubly linked list, we store the values and it hash maps we store the pointers of linked list nodes.

In case of a cache hit, we have to move the element to the front of the list. If the node is somewhere in the middle of doubly linked list, since we keep the pointers in the hash map and we retrieved in O(1) time, we can delete it by

  next_temp=retrieved_node.next
  prev_temp=retrieved_node.prev

then set the pointers to None

  retrieved_node.next=None
  retrieved_node.prev=None

and then you can reconnect the missing parts of the linked list

 prev_temp.next=next_temp

Woolpack